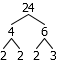
Another five minute challenge1, this time from /r/dailyprogrammer: given any positive integer, create and render a factor tree.
Another five minute challenge1, this time from /r/dailyprogrammer: given any positive integer, create and render a factor tree.
There was a new post on Programming Praxis a few days ago that seemed pretty neat:
Given a positive integer n, compute the prime factorization, including multiplicities, of n! = 1 · 2 · … · n. You should be able to handle very large n, which means that you should not compute the factorial before computing the factors, as the intermediate result will be extremely large.
Another post from Programming Praxis, from this past Tuesday:
The smallest pair of consecutive natural numbers that each have two distinct prime factors are 14 = 2 * 7 and 15 = 3 * 5. The smallest triplet of consecutive natural numbers that each have three distinct prime factors are 644 = 2^2 * 7 * 23, 645 = 3 * 5 * 43 and 646 = 2 * 17 * 19. What is the smallest set of four consecutive natural numbers that each have four distinct prime factors?
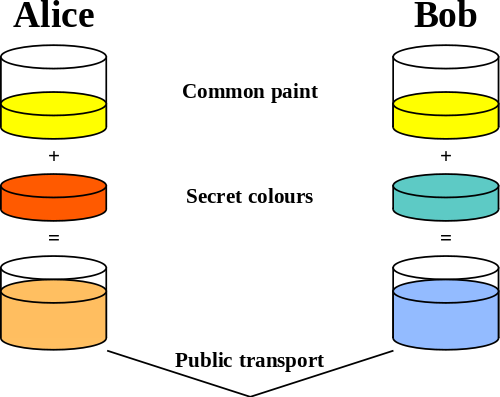
Today we’re going to be talking about cryptography, specifically Diffie-Hellman key exchange1. The basic idea isn’t necessarily to communicate in secret, but rather to establish the information that makes doing so much easier.
Yesterday’s post from Programming Praxis poses an interesting problem: find the largest prime n such that the result of repeatedly removing each digit of n from left to right is also always prime.
For example, 6317 would be such a number, as not only is it prime, but so are 317, 17, and 7.
After a sum of the first billion primes post (originally from Programming Praxis), I decided to finally write a segmented version of the Sieve of Eratosthenes.
This problem from Programming Praxis came about in the comments to my last post and intrigued me. So today, we are trying to sum the first one billion primes. Summing the first hundred, thousand, even million primes isn’t actually that bad. But it takes a bit more effort when you scale it up to a billion. And why’s that?
As the continuation of Saturday’s post on counting the number of prime partitions of a number without actually determining what those partitions are, today we’re going to work out the actual list of partitions.
Today we’re back into the mathy sort of problems from Programming Praxis, tasked with calculating the number of prime partitions for a given number–essentially, how many different lists of prime numbers are there that sum to the given number.
For example, working with 11, there are six prime partitions (I’ll show the code for this later):
> (prime-partitions 11)
'((2 2 2 2 3) (2 2 2 5) (2 2 7) (2 3 3 3) (3 3 5) (11))
Unfortunately, the number of prime partitions quickly gets ridiculous. Once you get to 1000, there are 48 quadrillion prime partitions… So generating all of them isn’t exactly feasible.