What feels like a million years and a lifetime ago, I wrote up a library for perlin and simple noise in Racket. Inspired by Jens Axel Søgaard’s new Sketching library (processing in Racket) and a conversation thereabout, I figure it’s about time to push noise to the raco package manager!
JP's Blog
Tupper's self-referential formula
Quick post today. Let’s implement Tupper's self-referential formula in Racket!
\frac{1}{2} < \left \lfloor mod \left ( \left \lfloor \frac{y}{17} 2^{-17 \lfloor x \rfloor - mod(\lfloor y \rfloor, 2)} \right \rfloor, 2 \right ) \right \rfloor
(tupper 960939379918958884971672962127852754715004339660129306651505519271702802395266424689642842174350718121267153782770623355993237280874144307891325963941337723487857735749823926629715517173716995165232890538221612403238855866184013235585136048828693337902491454229288667081096184496091705183454067827731551705405381627380967602565625016981482083418783163849115590225610003652351370343874461848378737238198224849863465033159410054974700593138339226497249461751545728366702369745461014655997933798537483143786841806593422227898388722980000748404719)
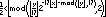
That’s the result of graphing the above function at a point rather far away from the origin. Specifically, where y is around that crazy big number. Look familiar?
Minimal palindromic base
What’s this? Two posts in one day? Well, writing a static blog generator can do that. 😄
Another easily phrased challenge:
We have a simple little problem today: Given an integer n > 2, find the minimum b > 1 for which n base b is a palindrome.
– Minimal Palindromic Base via Programming Praxis
Amicable chains
Mathematicians are an odd bunch. Names for just about everyhing. There are amicable numbers and perfect number, sociable number and betrothed numbers. There are sublime number, frugal number, and quasiperfect number. Heck, there are powerful number, smooth number, and even sphenic numbers. Rather a lot to deal with all told… So let’s just focus on two of them: perfect numbers and amicable numbers.
Trigonometric Triangle Trouble
Yesterday’s post at /r/dailyprogrammer managed to pique my interest1:
A triangle on a flat plane is described by its angles and side lengths, and you don’t need all of the angles and side lengths to work out everything about the triangle. (This is the same as last time.) However, this time, the triangle will not necessarily have a right angle. This is where more trigonometry comes in. Break out your trig again, people.
Crossing hands
Thirty second programming problem from Programming Praxis:
Your task is to write a progam that determines how many times the hands cross in one twelve-hour period, and compute a list of those times.
Ready?
Exploring parallelism in Racket with SHA-512 mining
While I’ve been getting a fair few programming exercises from Reddit’s /r/dailyprogrammer, more recently I’ve started following a few other sub-Reddits, such as /r/programming and /r/netsec. While browsing the former, I came across this intriguing gem of a problem: HashChallenge: can you find the lowest value SHA-512 hash?
Factoring factorials
There was a new post on Programming Praxis a few days ago that seemed pretty neat:
Given a positive integer n, compute the prime factorization, including multiplicities, of n! = 1 · 2 · … · n. You should be able to handle very large n, which means that you should not compute the factorial before computing the factors, as the intermediate result will be extremely large.
Graph coloring
Here’s another one from /r/dailyprogrammer:
… Your goal is to color a map of these regions with two requirements: 1) make sure that each adjacent department do not share a color, so you can clearly distinguish each department, and 2) minimize these numbers of colors.
Essentially, graph coloring.
Graph radius
Here’s a quick problem from the DailyProgrammer subreddit. Basically, we want to calculate the radius of a graph:
radius(g) = \min\limits_{n_0 \in g} \max\limits_{n_1 \in g} d_g(n_0, n_1)