About two weeks ago, I came across a post via /r/programming: Quadtree Art(src). In a sentence, the goal is to recursively divide an image into a quadtree, at each step expanding the current node with the largest internal variance.
JP's Blog
Programming, Topic: Data Structures
Recent posts (Page 5 of 6)
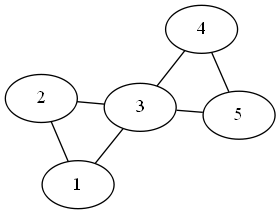
Graph coloring
Here’s another one from /r/dailyprogrammer:
… Your goal is to color a map of these regions with two requirements: 1) make sure that each adjacent department do not share a color, so you can clearly distinguish each department, and 2) minimize these numbers of colors.
Essentially, graph coloring.
Graph radius
Here’s a quick problem from the DailyProgrammer subreddit. Basically, we want to calculate the radius of a graph:
radius(g) = \min\limits_{n_0 \in g} \max\limits_{n_1 \in g} d_g(n_0, n_1)
Edges to adjacency
Another quick one, this time from /r/dailyprogrammer:
Your goal is to write a program that takes in a list of edge-node relationships, and print a directed adjacency matrix for it. Our convention will follow that rows point to columns. Follow the examples for clarification of this convention.
Functions as lists
Yesterday’s challenge from Programming Praxis challenges us to rebuild a data structure near and dear to any Lisper’s/Schemer’s/Racketer’s1/functional programmer’s heart: lists. The idea presented in their sample solution uses two element vectors, directly mimicking the general internal structure of Scheme’s lists. How about we do something a bit stranger? 😄
Large scale asynchronous DNS scans
On Monday we laid out a framework for converting structures into bytes. On Wednesday, we used that to enhance Racket’s UDP and DNS capabilities. Today, we’re going to take that all one step further and scan large portions of the Internet. The end goal will be to look for DNS-based on a worldwide scale.
Extending Racket's DNS capabilities
As I mentioned on Monday, I wrote my DNS-based censorship around the world–and to do that, I need a fair bit of control over the DNS packets that I’m sending back and over parsing the ones that I get back.
Extending Racket structs to bitfields
Keen eyed observers may have noticed that last Friday when I posted about converting my various Racket libraries to Planet 2 packages, that there was a new package there I haven’t otherwise talked about: bit-struct. Today seems like a good time to talk about that. Theoretically, I’ll also have another post or two this week showing exactly what I’m doing with it (spoilers: it involves sending on the order of billions of DNS requests1).
Cyclic equality
In today’s post from Programming Praxis, the goal is to check if two cyclic lists are equal. So if you have the cycles ↻(1 2 3 4 5) and ↻(3 4 5 1 2), they’re equal. Likewise, ↻(1 2 2 1) and ↻(2 1 1 2) are equal. But ↻(1 2 3 4) and ↻(1 2 3 5) are not since they have different elements while ↻(1 1 1) and ↻(1 1 1 1) aren’t since they have different elements.
Splay heaps redux-imperative model
I did say in yesterday’s comments that I would try re-implementing splay heaps using an imperative model with an array (Scheme’s vector) as the back end rather than a functional one with trees. Well, here is is.
All posts
- 2025-12-11: AoC 2025 Day 11: Graphinator
- 2024-12-22: AoC 2024 Day 22: Xorshiftinator
- 2024-12-05: AoC 2024 Day 5: (Not) Transitivinator
- 2023-08-12: StackLang Part IX: Better Testing
- 2023-08-11: StackLang Part VIII: Compiler Stacks
- 2023-08-05: StackLang Part VII: New CLI and Datatypes
- 2023-07-16: StackLang Part VI: Some Examples
- 2023-07-12: StackLang Part V: Compiling to C
- 2023-05-01: StackLang Part IV: An Interpreter
- 2023-04-24: StackLang Part III: The Parser
- 2023-04-16: StackLang Part II: The Lexer
- 2023-04-14: StackLang Part I: The Idea
- 2023-01-31: Cloning Redis in Rust: RESP [Part 1]
- 2022-12-21: AoC 2022 Day 21: Yellinator
- 2022-12-18: AoC 2022 Day 18: Lavinator
- 2022-12-08: AoC 2022 Day 8: Treetopinator
- 2022-12-06: AoC 2022 Day 6: Ring Buffinator
- 2022-12-05: AoC 2022 Day 5: Stackinator
- 2021-12-25: AoC 2021 Day 25: Cucumbinator
- 2021-12-24: AoC 2021 Day 24: Aluinator
- 2021-12-22: AoC 2021 Day 22: Cubinator
- 2021-12-20: AoC 2021 Day 20: Enhancinator
- 2021-12-19: AoC 2021 Day 19: Point Matchinator
- 2021-12-18: AoC 2021 Day 18: Pairs of Pairs
- 2021-12-16: AoC 2021 Day 16: Depacketinator
- 2021-12-12: AoC 2021 Day 12: Submarine Spider
- 2021-12-11: AoC 2021 Day 11: Octopus Flashinator
- 2021-12-10: AoC 2021 Day 10: Chunkinator
- 2021-12-09: AoC 2021 Day 9: Local Minimum Deminifier
- 2017-12-12: AoC 2017 Day 12: Gridlock
- 2017-12-07: AoC 2017 Day 7: Tree
- 2017-12-06: AoC 2017 Day 6: Tightrope
- 2017-12-03: AoC 2017 Day 3: Spiraly
- 2016-12-20: AoC 2016 Day 20: Filter Table
- 2016-12-11: AoC 2016 Day 11: Radiation Avoider
- 2015-01-29: iOS Backups in Racket: Apps
- 2015-01-27: iOS Backups in Racket: Messages
- 2015-01-23: iOS Backups in Racket: Contacts
- 2015-01-22: iOS Backups in Racket: Groundwork
- 2014-06-17: Factor trees
- 2014-05-28: Quadtree image compression
- 2014-01-15: Graph coloring
- 2014-01-14: Graph radius
- 2013-12-23: Edges to adjacency
- 2013-10-09: Functions as lists
- 2013-09-27: Large scale asynchronous DNS scans
- 2013-09-25: Extending Racket's DNS capabilities
- 2013-09-23: Extending Racket structs to bitfields
- 2013-04-09: Cyclic equality
- 2013-01-24: Splay heaps redux-imperative model
- 2013-01-23: Sorting via splay heap
- 2012-10-29: Bitvectors in Racket
- 2012-10-20: Memoization in Racket
- 2012-10-11: Dictionary tries in Racket
- 2012-10-08: Evaluating prefix/infix/postfix expressions
- 2012-10-07: Three ways to write expressions