Solving Sokobond

2024-04-06

Another solver that I’ve been working on, after A Good Snowman Is Hard To … Solve?. This time, we have Sokobond! It’s a Sokobon… but with chemical bonds! Yeah, that’s a really good title.

The basic idea is you have a field of elements with (chemical accurate) free electrons):

A basic level

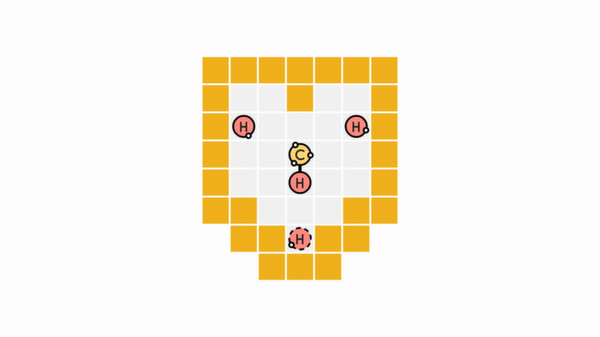
Here we have 4 hydrogens (1 bond each) and a carbon (4 bonds). It should seem pretty obvious that the carbon should end up with a hydrogen on each end. The one last bit of interest: the element with the dashed border is the one we actually control, that will never change.

This eventually gets more complicated, adding:

Modifiers that are placed on the map between squares:
- One that strengthens bonds, turning a single bond into double into triple
- One that weakens bonds, turning triple to double to single or breaking single bonds
- One that rotates bonds as you move by it
More elements, eventually hydrogen (1), oxygen (2), nitrogen (3), carbon (4), and helium (0)
Solutions that require forming multiple elements at the same time

It’s a pretty neat puzzle game with 144 levels of increasing difficulty. Perfect to solve.

A Good Snowman Is Hard To ... Solve?

2024-03-28

I enjoy puzzle games. I especially enjoy letting computers solve them for me 😄. Once upon a time, I set up a framework for solving random things. Let’s solve some more.

Today: A Good Snowman Is Hard To Build

It’s a Sokoban about making snowmen! You can push snowballs of three sizes around, collecting snow if you roll over it. You can push smaller snowballs onto bigger ones, stacking them. Or back off, in order to get around one another.

And that’s really it.

There are some interesting twists (multiple snowmen, the ability to leave and re-enter levels, and even a whole second ‘hard mode’), but at a basic level, it’s just pushing.

AoC 2022 Day 24: Blizzinator

2022-12-24

Source: Blizzard Basin

Part 1

Given a map with a series of moving walls (that wrap when the hit the edges of the simulation), calculate the fastest route from the top left to the bottom right.

AoC 2022 Day 23: Elf Scattinator

2022-12-23

Source: Unstable Diffusion

Part 1

Implement a cellular automaton with the following rules:

If you have no neighbors, don’t move (important, I forgot this one for a while)
Otherwise:
- Calculate a potential move:
  - If you have no neighbors to the north, move north
  - If not, check likewise for south, then west, than east
- If no other agent is moving to the same space, move to your potential move
- Otherwise, don’t move
On each frame, rotate the order the directions are checked in (NSWE, SWEN, WENS, ENSW, NSWE, …)

AoC 2022 Day 19: Blueprintinator

2022-12-19

Source: Not Enough Minerals

Part 1

Given a series of given a series of blueprints, each of which gives instructions for how to build a single robot from a collection of materials that in turn will produce one of a given material per turn, determine the best order of builds to maximize your geode (the most valuable material) production for each blueprint given a time limit of 24 minutes.

AoC 2022 Day 16: Pressurinator

2022-12-16

Source: Proboscidea Volcanium

Part 1

Given a graph of nodes, some of which have a pressure (per tick output value) and an agent that can move through the graph and activate specific nodes (so that they output their per tick value every future tick), what is the maximum total output possible in 30 steps?

AoC 2022 Day 15: Beaconator

2022-12-15

Source: Beacon Exclusion Zone

Part 1

There are a collections of Sensors and Beacons. As input, you are given the Beacon closest to each Sensor (using Manhattan Distance). If a Beacon is not closest to any sensor, it will not appear in this list. Calculate how many points in the given row (y=2000000) cannot contain a Beacon.