Yesterday’s challenge from Programming Praxis challenges us to rebuild a data structure near and dear to any Lisper’s/Schemer’s/Racketer’s1/functional programmer’s heart: lists. The idea presented in their sample solution uses two element vectors, directly mimicking the general internal structure of Scheme’s lists. How about we do something a bit stranger? 😄
JP's Blog
Programming, Language: Racket
Recent posts (Page 8 of 16)
Large scale asynchronous DNS scans
On Monday we laid out a framework for converting structures into bytes. On Wednesday, we used that to enhance Racket’s UDP and DNS capabilities. Today, we’re going to take that all one step further and scan large portions of the Internet. The end goal will be to look for DNS-based on a worldwide scale.
Extending Racket's DNS capabilities
As I mentioned on Monday, I wrote my DNS-based censorship around the world–and to do that, I need a fair bit of control over the DNS packets that I’m sending back and over parsing the ones that I get back.
Extending Racket structs to bitfields
Keen eyed observers may have noticed that last Friday when I posted about converting my various Racket libraries to Planet 2 packages, that there was a new package there I haven’t otherwise talked about: bit-struct. Today seems like a good time to talk about that. Theoretically, I’ll also have another post or two this week showing exactly what I’m doing with it (spoilers: it involves sending on the order of billions of DNS requests1).
Deploy Racket libraries to Planet 2
Over the last few years, I’ve managed to write a fair bit of Racket code. It’s a lovely language and an even better ecosystem for writing quick/clean code (batteries included!
). Several times throughout that, I’ve written code that I thought could be useful to others, including several libraries that I used to write my Racket Roguelike and code that I’ve used working with the C211 class at Indiana University. I’ve always said that I should turn these into packages that others can use and… I’ve finally figured it out.
Smallest consecutive four-factor composites
Another post from Programming Praxis, from this past Tuesday:
The smallest pair of consecutive natural numbers that each have two distinct prime factors are 14 = 2 * 7 and 15 = 3 * 5. The smallest triplet of consecutive natural numbers that each have three distinct prime factors are 644 = 2^2 * 7 * 23, 645 = 3 * 5 * 43 and 646 = 2 * 17 * 19. What is the smallest set of four consecutive natural numbers that each have four distinct prime factors?
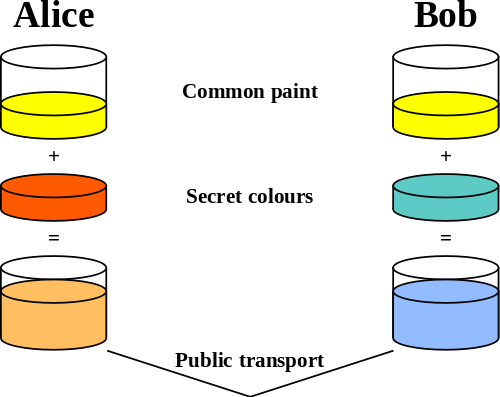
Diffie-Hellman Key Exchange
Today we’re going to be talking about cryptography, specifically Diffie-Hellman key exchange1. The basic idea isn’t necessarily to communicate in secret, but rather to establish the information that makes doing so much easier.
Visualizing the Monkey Grid
I’m a bit behind the times, but this post from Programming Praxis intrigued me enough that I kept it in my todo list for rather a while. So let’s get around to it.
I’ll just copy the description straight from the Programming Praxis website (although there are at least two previous version:[1][2]):
There is a monkey which can walk around on a planar grid. The monkey can move one space at a time left, right, up or down. That is, from (x, y) the monkey can go to (x+1, y), (x-1, y), (x, y+1), and (x, y-1). Points where the sum of the digits of the absolute value of the x coordinate plus the sum of the digits of the absolute value of the y coordinate are lesser than or equal to 19 are accessible to the monkey. For example, the point (59, 79) is inaccessible because 5 + 9 + 7 + 9 = 30, which is greater than 19. Another example: the point (-5, -7) is accessible because abs(-5) + abs(-7) = 5 + 7 = 12, which is less than 19. How many points can the monkey access if it starts at (0, 0), including (0, 0) itself?
'Tiny' Turing completeness without MMOV
Something was bugging me about my proof from yesterday. If we take another tack on proving Turing completeness, all we would have to prove is that we can simulate SUBLEQ. Since SUBLEQ is Turing complete, that’s all we need–just convert each SUBLEQ into a SUB, JZ, and a JLS. So that means that Tiny as written should be Turing complete.
So how does that work?
A 'Tiny' virtual machine in Racket
Today’s challenge at /r/dailyprogrammer asks to implement an assembler for a small virtual machine. It has only 16 mnemonics which in unique opcodes (each instruction can have multiple forms for if they’re accessing memory or literals), so it’s a simple virtual machine indeed. As a challenge, you’re supposed to write an interesting program (I actually wrote a virtual machine as well to test them). As an even better challenge, we’re supposed to prove that Tiny is Turing complete. Well, let’s get to it!
All posts
- 2021-08-05: raco pkg install noise
- 2020-01-29: Wrapping xattr as a racket module
- 2018-12-14: AoC 2018 Day 14: Functionally Circular Elfs
- 2018-12-13: AoC 2018 Day 13: Mine Cart Madness
- 2018-12-12: AoC 2018 Day 12: Fat Cellular Automaton
- 2018-12-11: AoC 2018 Day 11: Gridlocked Fuel
- 2018-12-10: AoC 2018 Day 10: It's Full of Stars!
- 2018-12-09: AoC 2018 Day 9: Marble Madness
- 2018-12-08: AoC 2018 Day 8: Checksum Treeification
- 2018-12-07: AoC 2018 Day 7: Job Simulator
- 2018-12-06: AoC 2018 Day 6: Infinite Area Simulator
- 2018-12-05: AoC 2018 Day 5: Alchemical reduction
- 2018-12-04: AoC 2018 Day 4: Sleeping on the job
- 2018-12-03: AoC 2018 Day 3: Regionification
- 2018-12-02: AoC 2018 Day 2: Counting letters
- 2018-12-01: AoC 2018 Day 1: Sum-thing to start with
- 2018-12-01: Advent of Code 2018
- 2015-05-07: Tupper's self-referential formula
- 2015-04-14: A Quick Look at RC4
- 2015-04-07: Generating perfect portmanteaus
- 2015-01-29: iOS Backups in Racket: Apps
- 2015-01-27: iOS Backups in Racket: Messages
- 2015-01-23: iOS Backups in Racket: Contacts
- 2015-01-22: iOS Backups in Racket: Groundwork
- 2015-01-09: Let it snow!
- 2015-01-01: Generating omnichromatic images
- 2014-12-23: Palette Swapping
- 2014-11-13: A "one" line echo server using let in Racket
- 2014-11-04: Clockception
- 2014-10-28: Tile Puzzle
- 2014-10-05: Regular Expression Fractals
- 2014-09-17: Invader Fractals
- 2014-09-16: Fractal Invaders
- 2014-09-15: Look and Say
- 2014-09-14: Procedural Invaders
- 2014-09-04: Chess Puzzles: Knight's Tour
- 2014-09-03: Chess Puzzles: N Queens
- 2014-08-28: Chess Puzzles 2: Board?
- 2014-08-21: Chess Puzzles 1: Get moving!
- 2014-08-13: Minimal palindromic base
- 2014-08-13: Number words
- 2014-08-07: Langton's ant
- 2014-07-10: Cracker Barrel Peg Game, Part 3
- 2014-07-09: Cracker Barrel Peg Game, Part 2
- 2014-07-05: Cracker Barrel Peg Game
- 2014-06-17: Factor trees
- 2014-06-11: Call stack bracket matcher
- 2014-06-10: What the (be)funge‽
- 2014-05-30: Braille unicode pixelation
- 2014-05-28: Quadtree image compression
- 2014-05-23: Amicable chains
- 2014-05-21: Phone networks
- 2014-05-19: Novel compression
- 2014-05-02: Trigonometric Triangle Trouble
- 2014-04-01: Gorellian sorting
- 2014-03-12: Caesar cipher
- 2014-03-11: Brownian trees
- 2014-02-27: Dis/re-emvowelification
- 2014-02-27: Crossing hands
- 2014-02-16: Exploring parallelism in Racket with SHA-512 mining
- 2014-01-27: Factoring factorials
- 2014-01-15: Graph coloring
- 2014-01-14: Graph radius
- 2014-01-03: Overlapping circles
- 2013-12-23: Edges to adjacency
- 2013-12-21: Rock-paper-scissors
- 2013-11-30: Twitter puddle
- 2013-11-12: Making music, part 3: Making noise
- 2013-11-07: Making music, part 2: Taking shape
- 2013-10-29: Making music, part 1: Reading ABC notation
- 2013-10-09: Functions as lists
- 2013-09-27: Large scale asynchronous DNS scans
- 2013-09-25: Extending Racket's DNS capabilities
- 2013-09-23: Extending Racket structs to bitfields
- 2013-09-20: Deploy Racket libraries to Planet 2
- 2013-09-19: Smallest consecutive four-factor composites
- 2013-09-14: Diffie-Hellman Key Exchange
- 2013-08-30: Visualizing the Monkey Grid
- 2013-08-22: 'Tiny' Turing completeness without MMOV
- 2013-08-21: A 'Tiny' virtual machine in Racket
- 2013-08-06: Adventures in Racket: gzip
- 2013-08-06: Authorship attribution: Part 3
- 2013-08-02: Authorship attribution: Part 2
- 2013-07-30: Authorship attribution: Part 1
- 2013-07-19: Racket Roguelike: Post-mortem
- 2013-07-05: Racket Roguelike 10: Levels via automata!
- 2013-06-29: A programming puzzle: f(f(n)) = -n
- 2013-06-28: Racket Roguelike 9: Daedalus' wrath!
- 2013-06-26: Swap list nodes
- 2013-06-21: Racket Roguelike 8: A million words!
- 2013-05-24: Racket Roguelike - Going on hiatus
- 2013-05-17: Racket Roguelike 7: Into darkness!
- 2013-05-10: Racket Roguelike 6: Dig deeper!
- 2013-05-02: Racket Roguelike 5: Armors and weapons and potions, oh my!
- 2013-04-25: Racket Roguelike 4: Slightly smarter critters!
- 2013-04-23: User space continuation-based thread pool
- 2013-04-18: Racket Roguelike 3: Rats, rats, everywhere!
- 2013-04-18: A prototype object system for Racket
- 2013-04-16: Adventures in optimization, re: Typed Racket
- 2013-04-11: Racket Roguelike 2: Infinite caves!
- 2013-04-11: Perlin and simplex noise in Racket
- 2013-04-09: Cyclic equality
- 2013-04-04: Racket Roguelike 1: A GUI, screens, I/O, and you!
- 2013-03-28: Writing a roguelike - in Racket! (Day 0)
- 2013-03-28: Path to philosophy
- 2013-03-17: The House on the Hill - Postmortem
- 2013-03-16: The House on the Hill - Day 5
- 2013-03-15: The House on the Hill - Day 4
- 2013-03-14: The House on the Hill - Day 3
- 2013-03-13: The House on the Hill – Day 2
- 2013-03-12: The House on the Hill - Day 1
- 2013-03-11: Knight moves
- 2013-03-06: Partitioning the Dutch national flag
- 2013-02-22: Making Floupian Change
- 2013-02-20: NPR Sunday Puzzle
- 2013-02-13: Predecessor and successor in a binary search tree
- 2013-02-06: Numbers as words in arbitrary bases
- 2013-02-06: The 147 Puzzle
- 2013-01-25: An optimal alphabetizing cipher
- 2013-01-25: Gregorian/Mayan conversion
- 2013-01-24: Splay heaps redux-imperative model
- 2013-01-23: Sorting via splay heap
- 2013-01-20: Triangle Trilemma
- 2013-01-16: Translate CSV to HTML
- 2013-01-03: Four points, a square?
- 2013-01-02: Happy New Year
- 2012-12-31: Parallel BF
- 2012-12-30: A Brainf**k Interpreter
- 2012-12-22: Nested Primes
- 2012-12-14: Narcissistic Numbers
- 2012-12-12: Generating non-repeating strings
- 2012-12-10: Numbers of Wirth
- 2012-11-29: One Billion Primes - Segmented Sieve
- 2012-11-21: List algorithms and efficiency
- 2012-11-15: Project Euler 9
- 2012-11-14: Project Euler 8
- 2012-11-12: Project Euler 7
- 2012-11-11: Project Euler 6
- 2012-11-10: Taxicab numbers
- 2012-11-08: Project Euler 5
- 2012-11-07: Project Euler 4
- 2012-11-04: Project Euler 2
- 2012-11-03: Project Euler 1
- 2012-11-01: The Sum Of The First Billion Primes
- 2012-10-31: Pandigital Sums
- 2012-10-29: Bitvectors in Racket
- 2012-10-27: Pythagorean Triples
- 2012-10-22: Prime Partitions II: The Listing
- 2012-10-20: Prime Partitions
- 2012-10-20: Memoization in Racket
- 2012-10-18: The Evolution Of Flibs
- 2012-10-17: Rule 30 RNG
- 2012-10-15: Chopping words
- 2012-10-14: Dodgson’s Doublets
- 2012-10-13: Word cubes
- 2012-10-11: Squaring the Bishop
- 2012-10-11: Dictionary tries in Racket
- 2012-10-10: Two Word Games
- 2012-09-19: A piece of the abc conjecture
- 2012-09-16: A needle in a Pi-stack