JP's Blog
Programming, Language: Javascript
Recent posts (Page 5 of 10)
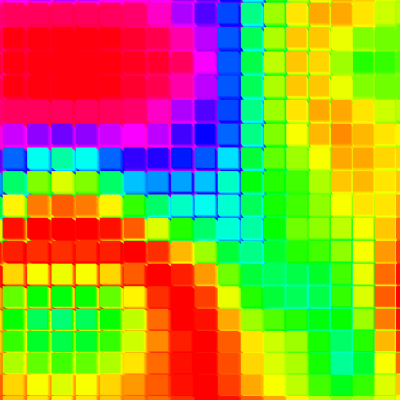
Genuary 2023.15: Sine Waves
Spend a month making one beautiful thing per day, given a bunch of prompts. A month late, but as they say, ’the second best time is now'.
Let’s do it!
15) Sine waves
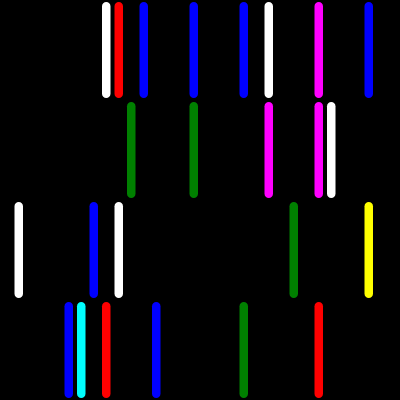
Genuary 2023.14: Asemic Writing
Spend a month making one beautiful thing per day, given a bunch of prompts. A month late, but as they say, ’the second best time is now'.
Let’s do it!
14) Asemic writing
Wikipedia: Asemic writing
Use the same Wikipedia code as yesterday to get a random page, render each word as a line that meanders based on the letters of the word. Shiny. 😄
Genuary 2023.13: Something you've always wanted to learn
Spend a month making one beautiful thing per day, given a bunch of prompts. A month late, but as they say, ’the second best time is now'.
Let’s do it!
13) Something you’ve always wanted to learn
META! LEARN EVERYTHING!
Fetch a random page from Wikipedia and scroll it by super quick, see how fast you can speed read it. And heck, you might just learn something. I know I did!
let url;
let titleToRender;
let wordsToRender;
let wordIndex;
let nextButton;
let wikiButton;
const CHAR_SIZE = 60;
function setup() {
createCanvas(400, 400);
frameRate(10);
nextButton = createButton("next");
nextButton.mousePressed(renderRandomPage);
wikiButton = createButton("open");
wikiButton.mousePressed(() => {
window.open(url, '_blank');
});
wordsToRender = [];
wordIndex = 0;
renderRandomPage();
}
function draw() {
if (wordIndex > wordsToRender.length) {
noLoop();
}
clear();
textSize(CHAR_SIZE);
for (let i = 0; i < height / CHAR_SIZE; i++) {
if (i == 3) {
fill("black");
} else {
fill("lightgray");
}
text(
wordsToRender[wordIndex + i],
10,
CHAR_SIZE * (i + 1)
);
}
stroke("black");
line(
width - 10,
10,
width - 10,
height - 10
);
circle(
width - 10,
1.0 * wordIndex / wordsToRender.length * (height - 20),
20
);
wordIndex++;
}
function renderRandomPage() {
wikiButton.attribute('disabled', '');
// https://stackoverflow.com/a/70225116
async function go() {
let title;
{
let json = await httpGet(`https://en.wikipedia.org/w/api.php?action=query&format=json&generator=random&grnlimit=1&grnnamespace=0&prop=info&origin=*`, 'json');
let pages = json.query.pages;
let id = Object.keys(pages)[0];
title = pages[id].title;
url = `https://en.wikipedia.org/wiki/${title}`;
}
let body;
{
let json = await httpGet(`https://en.wikipedia.org/w/api.php?action=query&format=json&titles=${title}&prop=extracts&explaintext&origin=*`, 'json');
let pages = json.query.pages;
let id = Object.keys(pages)[0];
body = pages[id].extract;
}
return [title, body];
}
background(255);
text("Loading...", 10, 20);
go().then(([title, body]) => {
titleToRender = title;
wordsToRender = body.trim().split(/\s+/);
wordIndex = 0;
wikiButton.removeAttribute('disabled');
loop();
});
}
Genuary 2023.12: Tessellation
Spend a month making one beautiful thing per day, given a bunch of prompts. A month late, but as they say, ’the second best time is now'.
Let’s do it!
12) Tessellation
Wikipedia: Tessellation (List)
This was not at all the direction I ended to go, but it got really interesting, so I decided to keep it.
What I remember doing years and years ago, I think roughly around the time of Windows 95 (I feel old) or perhaps even pre-Windows was using a tesselation program that would give you a basic shape and then allow you to pull the edges in a way it would propagate to automatically keep the tesselation valid. It was pretty awesome… but I have no idea what it was called any more.
It might have been Shodor on Tessellations.org, or perhaps TesselMania!. Been a while.
In any case, enjoy!
const SIZE = 40;
let gui;
let params = {
scale: 1.0, scaleMin: 0.25, scaleMax: 3.0, scaleStep: 0.01,
drawBorders: true,
applyRotation: true,
fastFlux: true,
varyRotations: true,
}
let g;
let buffer;
let bufferMask;
let lastRedrawBuffer;
function setup() {
createCanvas(400, 400);
g = createGraphics(width, height);
buffer = createGraphics(2 * SIZE, 2 * SIZE);
for (let i = 0; i < 100; i++) {
buffer.fill(
255 * random(),
255 * random(),
255 * random(),
255 * random()
);
buffer.rect(
random(4 * SIZE) - 2 * SIZE,
random(4 * SIZE) - 2 * SIZE,
random(2 * SIZE),
random(2 * SIZE)
)
}
redrawBuffer();
bufferMask = createGraphics(2 * SIZE, 2 * SIZE);
bufferMask.push();
{
bufferMask.translate(SIZE, SIZE);
bufferMask.scale(params.scale);
bufferMask.stroke("black");
bufferMask.fill("black");
ngon(bufferMask, 6, SIZE);
}
bufferMask.pop();
gui = createGuiPanel('params');
gui.addObject(params);
gui.setPosition(420, 0);
}
function draw() {
g.background(255);
if (params.fastFlux) {
drawOneToBuffer();
} else {
if (millis() - lastRedrawBuffer > 1000) {
redrawBuffer();
}
}
let masked = buffer.get();
masked.mask(bufferMask);
g.push();
{
g.stroke("black");
g.fill("green");
g.translate(200, 200);
g.scale(params.scale);
g.stroke("black");
g.noFill();
if (params.drawBorders) {
g.stroke("black");
g.strokeWeight(2);
ngon(g, 6, SIZE);
}
g.push();
{
g.translate(-SIZE, -SIZE);
g.image(masked, 0, 0);
}
g.pop();
for (let xd = -10; xd < 10; xd++) {
for (let yd = -50; yd < 50; yd++) {
if (xd == 0 && yd == 0) continue;
g.push();
{
let rowOffset = abs(yd) % 2 == 1 ? 1.5 * SIZE : 0;
// Major thanks to:
// https://www.redblobgames.com/grids/hexagons/
g.translate(
rowOffset + 3.0 * xd * SIZE,
sqrt(3) / 2 * yd * SIZE
);
if (params.applyRotation) {
let n = noise(
xd,
yd,
params.varyRotations ? frameCount / 500.0 : 0
);
g.rotate(TWO_PI / 6.0 * parseInt(n * 6));
}
g.push();
{
g.translate(-SIZE, -SIZE);
g.image(masked, 0, 0);
}
g.pop();
if (params.drawBorders) {
g.stroke("black");
g.strokeWeight(2);
ngon(g, 6, SIZE);
}
}
g.pop();
}
}
}
g.pop();
image(g, 0, 0);
}
function ngon(g, n, size) {
g.beginShape();
for (let i = 0; i < n; i++) {
let x = size * cos(TWO_PI * i / n);
let y = size * sin(TWO_PI * i / n);
g.vertex(x, y);
}
g.endShape(CLOSE);
}
function redrawBuffer() {
buffer.background(255);
for (let i = 0; i < 100; i++) {
drawOneToBuffer();
}
lastRedrawBuffer = millis();
}
function drawOneToBuffer() {
buffer.fill(
255 * random(),
255 * random(),
255 * random(),
255 * random()
);
buffer.rect(
random(4 * SIZE) - 2 * SIZE,
random(4 * SIZE) - 2 * SIZE,
random(2 * SIZE),
random(2 * SIZE)
);
}
Genuary 2023.11: Suprematism
Spend a month making one beautiful thing per day, given a bunch of prompts. A month late, but as they say, ’the second best time is now'.
Let’s do it!
11) Suprematism
Wikipedia: Suprematism
Genuary 2023.10: Generative Music
Spend a month making one beautiful thing per day, given a bunch of prompts. A month late, but as they say, ’the second best time is now'.
Let’s do it!
10) Generative music
Wikipedia: Generative music
NOTE: Because of limitations in JavaScript autoplaying sound, you must click to start.
NOTE: This currently doesn’t work in Safari. Something funny with the p5.sound addon. I’m working on it.
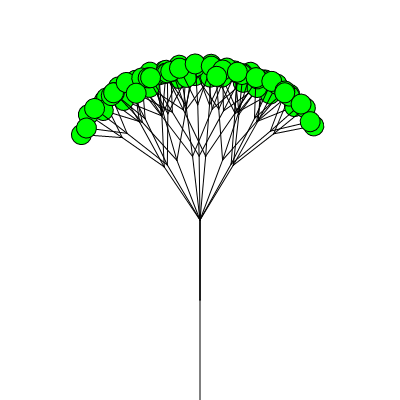
Genuary 2023.09: Plants
Spend a month making one beautiful thing per day, given a bunch of prompts. A month late, but as they say, ’the second best time is now'.
Let’s do it!
9) Plants
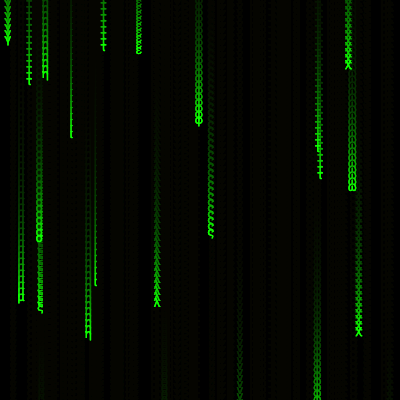
Genuary 2023.08: Signed Distance Functions
Spend a month making one beautiful thing per day, given a bunch of prompts. A month late, but as they say, ’the second best time is now'.
Let’s do it!
8) Signed Distance Functions
Genuary 2023.07: Sample a color palette
Spend a month making one beautiful thing per day, given a bunch of prompts. A month late, but as they say, ’the second best time is now'.
Let’s do it!
7) Sample a color palette from your favorite movie/album cover
All posts
- 2026-01-22: Genuary 2026.22: Pen plotter ready
- 2026-01-21: Genuary 2026.21: Bauhaus poster
- 2026-01-20: Genuary 2026.20: One line
- 2026-01-19: Genuary 2026.19: 16x16
- 2026-01-18: Genuary 2026.18: Unexpected paths
- 2026-01-17: Genuary 2026.17: Wallpaper Groups
- 2026-01-16: Genuary 2026.16: Order vs Disorder
- 2026-01-15: Genuary 2026.15: Invisible Object
- 2026-01-14: Genuary 2026.14: Fits Perfectly
- 2026-01-13: Genuary 2026.13: Self Portrait
- 2026-01-12: Genuary 2026.12: Boxes
- 2026-01-11: Genuary 2026.11: Quine
- 2026-01-10: Genuary 2026.10: Polar coordinates
- 2026-01-09: Genuary 2026.09: Cellular automata
- 2026-01-08: Genuary 2026.08: A city
- 2026-01-07: Genuary 2026.07: Boolean algebra
- 2026-01-06: Genuary 2026.06: Lights on/off
- 2026-01-05: Genuary 2026.05: Write 'genuary'
- 2026-01-04: Genuary 2026.04: lowres
- 2026-01-03: Genuary 2026.03: Fibonacci forever
- 2026-01-02: Genuary 2026.02: Twelve principles of animation
- 2026-01-01: Genuary 2026.01: One color, one shape
- 2025-12-20: Locking BGA tabs with UserScripts
- 2025-05-29: Parsing PEM Certificates & ASN.1 in Javascript
- 2025-02-05: WebCrypto SHA-256 HMAC
- 2023-03-03: Genuary 2023.31: Break a previous image
- 2023-03-02: Genuary 2023.30: Minimalism
- 2023-03-01: Genuary 2023.29: Maximalism
- 2023-02-28: Genuary 2023.28: Generative poetry
- 2023-02-27: Genuary 2023.27: In the style of Hilma Af Klint
- 2023-02-26: Genuary 2023.26: My kid could have made that
- 2023-02-25: Genuary 2023.25: Yayoi Kusama
- 2023-02-24: Genuary 2023.24: Textile
- 2023-02-23: Genuary 2023.23: Moiré
- 2023-02-22: Genuary 2023.22: Shadows
- 2023-02-21: Genuary 2023.21: Persian Carpet
- 2023-02-20: Genuary 2023.20: Art Deco
- 2023-02-19: Genuary 2023.19: Black and white
- 2023-02-18: Genuary 2023.18: Definitely not a grid
- 2023-02-17: Genuary 2023.17: A grid inside a grid inside a grid
- 2023-02-16: Genuary 2023.16: Reflections of a Reflection
- 2023-02-15: Genuary 2023.15: Sine Waves
- 2023-02-14: Genuary 2023.14: Asemic Writing
- 2023-02-13: Genuary 2023.13: Something you've always wanted to learn
- 2023-02-12: Genuary 2023.12: Tessellation
- 2023-02-11: Genuary 2023.11: Suprematism
- 2023-02-10: Genuary 2023.10: Generative Music
- 2023-02-09: Genuary 2023.09: Plants
- 2023-02-08: Genuary 2023.08: Signed Distance Functions
- 2023-02-07: Genuary 2023.07: Sample a color palette
- 2023-02-06: Genuary 2023.06: Steal like an artist
- 2023-02-05: Genuary 2023.05: Debug view
- 2023-02-04: Genuary 2023.04: Intersections
- 2023-02-03: Genuary 2023.03: Glitch art
- 2023-02-02: Genuary 2023.02: Made in 10 minutes
- 2023-02-01: Genuary 2023.01: Perfect loop
- 2023-01-19: Local JS/CSS with Hugo Pipe
- 2022-08-29: Runelang: A Summoning Circle Generator
- 2022-08-25: Runelang: A Bind Rune Generator
- 2022-07-16: Runelang: Evaluation
- 2022-03-18: Runelang: The Parser (Part 2: Expressions)
- 2022-03-15: Runelang: The Parser (Part 1)
- 2022-02-24: Runelang: The Lexer
- 2022-02-23: Runelang: Language Specification
- 2021-09-06: Neural Network Cellular Automata
- 2021-08-18: Solving Snakebird
- 2021-08-17: Immutable.js Solvers
- 2021-06-25: A Generic Brute Force Backtracking Solver
- 2021-01-25: GMail Oldest First
- 2021-01-08: Genuary: Triple Nested Loops
- 2020-12-11: Pictogenesis: Stack Transpiling
- 2020-12-09: Pictogenesis: Stack Machine
- 2020-12-03: Pictogenesis: Transpiling
- 2020-12-01: Pictogenesis: Wrapping Modes
- 2020-11-24: Pictogenesis: Register Machine
- 2020-11-23: Pictogenesis: The Idea
- 2020-11-20: Backtracking Worm Coral
- 2020-11-19: Worm Coral
- 2020-11-18: p5js Boids
- 2020-11-17: p5js Worms
- 2019-05-02: Prevent JavaScript links by parsing URLs
- 2019-01-04: Listing and Downloading S3 Versions
- 2018-09-26: Simple LocalStorage Notepad
- 2016-01-02: Inlining plaintext attachments in Gmail
- 2014-08-24: Sandbox Battle!
- 2014-08-24: Ludum Dare 30: Demo mode
- 2014-08-23: Ludum Dare 30: Programmer art and simple AI
- 2014-08-23: Ludum Dare 30: 24 hours
- 2014-08-23: Ludum Dare 30: Hints of a game
- 2014-08-22: Ludum Dare 30: Sandbox Battle
- 2014-01-13: CSRF protection injection with jQuery and Zend
- 2013-03-18: Approximating Pi with Buffon's Needle
- 2013-03-06: Partitioning the Dutch national flag
- 2012-10-08: Evaluating prefix/infix/postfix expressions
- 2012-10-03: Elementary cellular automaton
- 2012-10-01: The Birthday Paradox
- 2012-09-27: HTML5 Bugs
- 2012-09-26: Line art with an HTML5 canvas
- 2012-09-20: Playing with loaded dice
- 2012-09-17: Who wants to win the lottery?