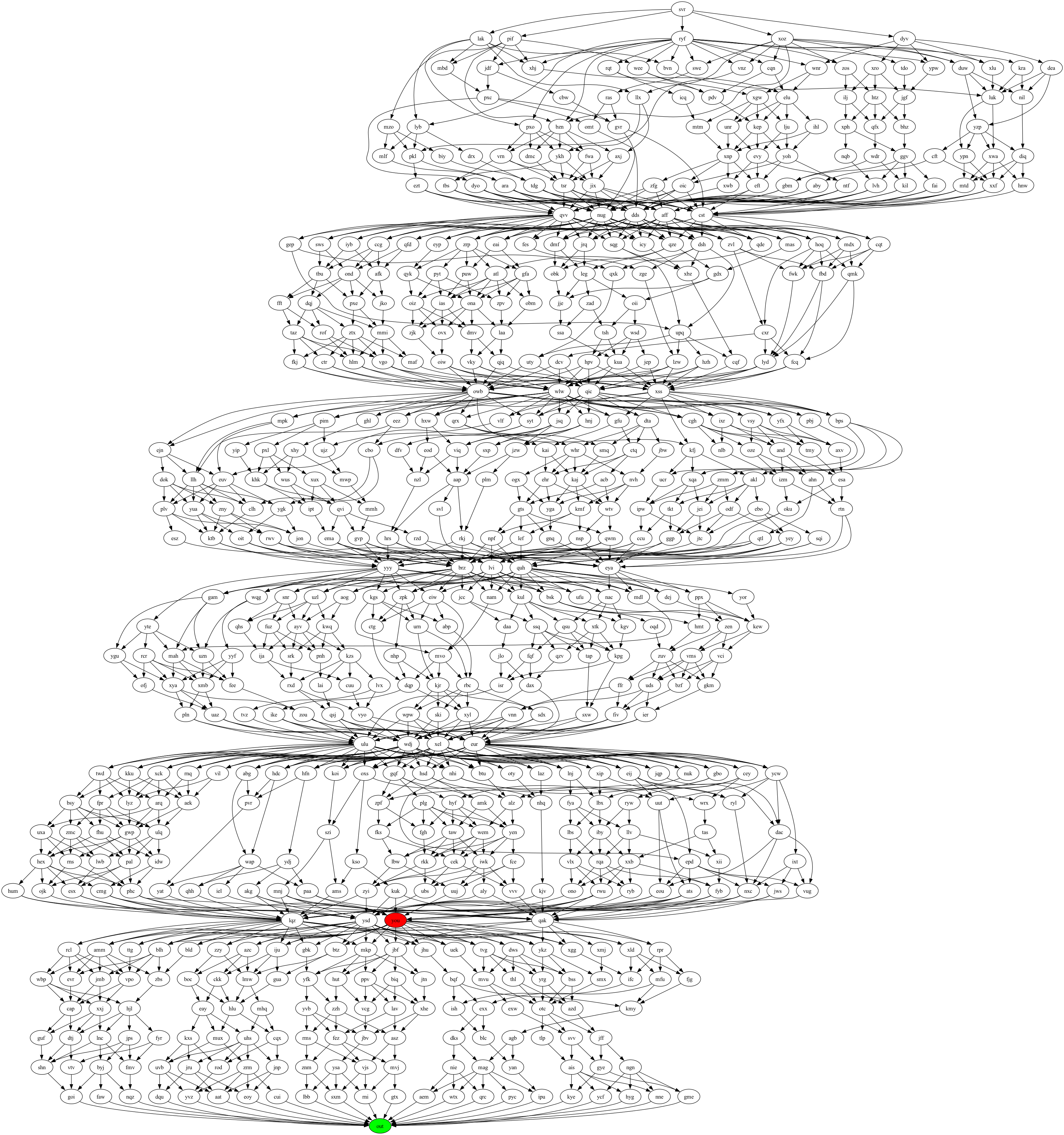
Source: Day 11: Reactor
Full solution for today (spoilers!).
Part 1
Given a directed graph defined where
aaa: you hhhmeansaaais connected toyouandhhh, how many paths are there fromyoutoout.
Well, since we assume the number of paths is finite, I expect this is more like a tree than a graph. Or rather a DAG.
You can see this:
$ (\
echo '
digraph {
you [style=filled fillcolor=red]
out [style=filled fillcolor=green]
' \
&& cat input/2025/day11.txt | awk '
{
key=$1;
sub(/:$/, "", key);
for (i=2; i<=NF; i++)
print key " -> " $i
}
' \
&& echo '}' \
) | dot -Tpng -o aoc2025_day11_part1.png
(Click for the full version)
It’s not very pretty, but you can see the structure. You have a set of 6 tiers, each of which have a few (4-5) nodes in between that all paths cross through. But, you is right before the last tier, so we can just solve this recursively (and you can guess what part 2 will be 😄):
#[aoc::register]
fn part1(input: &str) -> impl Into<String> {
let mut outputs = HashMap::new();
for line in input.lines() {
let (src, dsts) = line.split_once(": ").unwrap();
for dst in dsts.split_whitespace() {
outputs.entry(src).or_insert_with(Vec::new).push(dst);
}
}
// Assuming no loops
fn paths(outputs: &HashMap<&str, Vec<&str>>, src: &str, dst: &str) -> usize {
if src == dst {
return 1;
}
let mut total = 0;
if let Some(dsts) = outputs.get(src) {
for next in dsts {
total += paths(outputs, next, dst);
}
}
total
}
paths(&outputs, "you", "out").to_string()
}
Which works well enough:
$ just run-and-bench 11 part1
796
part1: 143.184µs ± 77.932µs [min: 117.125µs, max: 868.583µs, median: 132.709µs]
Part 2
Go from
svrtooutand pass through bothdacandfft.
$ (\
echo '
digraph {
svr [style=filled fillcolor=red]
dac [style=filled fillcolor=blue]
fft [style=filled fillcolor=blue]
out [style=filled fillcolor=green]
' \
&& cat input/2025/day11.txt | awk '
{
key=$1;
sub(/:$/, "", key);
for (i=2; i<=NF; i++)
print key " -> " $i
}
' \
&& echo '}' \
) | dot -Tpng -o aoc2025_day11_part2.png
Okay, so this time, we have to go through the whole thing. One thing that we know, because of the structure of the graph, is that at any particular point along the path, there are a ton of ways you could get from there to the end, so it’s a perfect candidate for dynamic programming or memoization.
#[aoc::register]
fn part2_memo(input: &str) -> impl Into<String> {
let mut outputs = HashMap::new();
let mut ids = vec![];
for line in input.lines() {
let (src, dsts) = line.split_once(": ").unwrap();
if !ids.contains(&src) {
ids.push(src);
}
let src_id = ids.iter().position(|&x| x == src).unwrap();
for dst in dsts.split_whitespace() {
if !ids.contains(&dst) {
ids.push(dst);
}
let dst_id = ids.iter().position(|&x| x == dst).unwrap();
outputs.entry(src_id).or_insert_with(Vec::new).push(dst_id);
}
}
// Still assuming no loops
// This time, we have to go from src to dst and hit all of targets
// We'll memoize on (src, dst, remaining targets)
// In order to memoize and not deal with lifetimes, we'll use indices instead of &strs
fn paths(
outputs: &HashMap<usize, Vec<usize>>,
src: usize,
dst: usize,
targets: &Vec<usize>,
memo: &mut HashMap<(usize, usize, Vec<usize>), usize>,
) -> usize {
if let Some(&cached) = memo.get(&(src, dst, targets.clone())) {
return cached;
}
// If we're at the dst, we're done either way
// If we did visit all the targets, this is a valid path
// If not, this is not a valid path, so recur up a zero!
if src == dst {
if targets.is_empty() {
return 1;
} else {
return 0;
}
}
// Side path: if we're on a target node, remove it from targets
if targets.contains(&src) {
let mut new_targets = targets.clone();
new_targets.retain(|&x| x != src);
return paths(outputs, src, dst, &new_targets, memo);
}
// Otherwise, recur
let mut total = 0;
if let Some(dsts) = outputs.get(&src) {
for next in dsts {
total += paths(outputs, *next, dst, targets, memo);
}
}
memo.insert((src, dst, targets.clone()), total);
total
}
let svr_id = ids.iter().position(|&x| x == "svr").unwrap();
let out_id = ids.iter().position(|&x| x == "out").unwrap();
let dac_id = ids.iter().position(|&x| x == "dac").unwrap();
let fft_id = ids.iter().position(|&x| x == "fft").unwrap();
paths(
&outputs,
svr_id,
out_id,
&vec![dac_id, fft_id],
&mut HashMap::new(),
)
.to_string()
}
One change that I had to do here was to use usize for all of the IDs rather than &str. This avoids allocating a bunch of String while at the same time, letting us have a pretty quick cache.
I did generalize for any number of targets rather than just 2, which I thought was neat. If you want it to run faster, a pair of bool variables for has_seen_dac etc would probably be faster.
But still:
$ just run-and-bench 11 part2_memo
294053029111296
part2_memo: 4.288263ms ± 144.887µs [min: 4.137417ms, max: 4.72625ms, median: 4.241917ms]
Benchmarks
$ just bench 11
part1: 127.686µs ± 3.013µs [min: 121.542µs, max: 144.167µs, median: 127.334µs]
part2_memo: 4.545146ms ± 78.356µs [min: 4.165917ms, max: 4.687ms, median: 4.563333ms]
| Day | Part | Solution | Benchmark |
|---|---|---|---|
| 11 | 1 | part1 | 127.686µs ± 3.013µs |
| 11 | 2 | part2_memo | 4.545146ms ± 78.356µs |