Source: Day 9: Movie Theater
Full solution for today (spoilers!).
Part 1
Given a list of points (2D), find the pair of points which form the largest rectangle.
#[aoc::register]
fn part1(input: &str) -> impl Into<String> {
let points = input.lines().map(Point2D::from).collect::<Vec<_>>();
let mut max_area = 0;
for i in 0..points.len() {
for j in i + 1..points.len() {
let xd = (points[i].x - points[j].x).abs() + 1;
let yd = (points[i].y - points[j].y).abs() + 1;
let area = xd * yd;
if area > max_area {
max_area = area;
}
}
}
max_area.to_string()
}
I expect you could estimate a bit more by looking at the points, but honestly, this works fine.
$ just run-and-bench 9 part1
4749929916
part1: 117.402µs ± 5.432µs [min: 108.583µs, max: 146.583µs, median: 117.791µs]
Part 2
The points define a polygon. Find the largest rectangle made by two points that lies entirely within the polygon.
Well isn’t that fun.
At the very least it’s worth making a few helper classes:
line2d.rs
#[derive(Debug, Copy, Clone, PartialEq, Eq, Hash)]
pub struct Line2D {
start: Point2D,
end: Point2D,
}
impl Line2D {
pub fn new(start: Point2D, end: Point2D) -> Self {
Line2D { start, end }
}
pub fn intersects(&self, other: &Line2D) -> bool {
let d1 = (self.end.x - self.start.x) * (other.start.y - self.start.y)
- (self.end.y - self.start.y) * (other.start.x - self.start.x);
let d2 = (self.end.x - self.start.x) * (other.end.y - self.start.y)
- (self.end.y - self.start.y) * (other.end.x - self.start.x);
let d3 = (other.end.x - other.start.x) * (self.start.y - other.start.y)
- (other.end.y - other.start.y) * (self.start.x - other.start.x);
let d4 = (other.end.x - other.start.x) * (self.end.y - other.start.y)
- (other.end.y - other.start.y) * (self.end.x - other.start.x);
if ((d1 > 0 && d2 < 0) || (d1 < 0 && d2 > 0)) && ((d3 > 0 && d4 < 0) || (d3 < 0 && d4 > 0))
{
return true;
}
false
}
}
Why, yes. I did write test cases for that. It’s bonkers looking.
polygon.rs
#[derive(Debug, Clone)]
pub struct Polygon {
vertices: Vec<Point2D>,
}
impl Polygon {
pub fn new(vertices: Vec<Point2D>) -> Self {
Polygon { vertices }
}
// Check if a point is inside the polygon using the ray-casting algorithm
// Source: https://www.xjavascript.com/blog/check-if-polygon-is-inside-a-polygon/
pub fn contains(&self, point: &Point2D) -> bool {
let mut inside = false;
let n = self.vertices.len();
for i in 0..n {
let j = (i + n - 1) % n;
let pi = &self.vertices[i];
let pj = &self.vertices[j];
// TODO: On edge check
if (pi.y > point.y) != (pj.y > point.y) {
let x_intersect = (pj.x - pi.x) * (point.y - pi.y) / (pj.y - pi.y) + pi.x;
if point.x < x_intersect {
inside = !inside;
}
}
}
inside
}
}
I ended up working around the edge check in this case, so I’ll implement that later if we need it.
Back to the problem
#[aoc::register]
fn part2(input: &str) -> impl Into<String> {
let points = input.lines().map(Point2D::from).collect::<Vec<_>>();
let polygon = Polygon::new(points.clone());
let mut max_area = 0;
for i in 0..points.len() {
for j in i + 1..points.len() {
// All 4 vertices must be within the polygon
// Because the polygons are on a grid of points, this means we can ignore the edge checks
// This will skip rectangles with width/height = 1, but those won't be max area (we assume)
let vertices = [
Point2D::new(
points[i].x.min(points[j].x) + 1,
points[i].y.min(points[j].y) + 1,
),
Point2D::new(
points[i].x.min(points[j].x) + 1,
points[i].y.max(points[j].y) - 1,
),
Point2D::new(
points[i].x.max(points[j].x) - 1,
points[i].y.min(points[j].y) + 1,
),
Point2D::new(
points[i].x.max(points[j].x) - 1,
points[i].y.max(points[j].y) - 1,
),
];
if !vertices.iter().all(|v| polygon.contains(v)) {
continue;
}
// No edge of the rectangle can intersect with any edge of the polygon
let rectangle_edges = vec![
Line2D::new(vertices[0], vertices[1]),
Line2D::new(vertices[1], vertices[3]),
Line2D::new(vertices[3], vertices[2]),
Line2D::new(vertices[2], vertices[0]),
];
let mut intersects = false;
'outer: for rect_edge in &rectangle_edges {
for i in 0..points.len() {
let poly_edge = Line2D::new(points[i], points[(i + 1) % points.len()]);
if rect_edge.intersects(&poly_edge) {
intersects = true;
break 'outer;
}
}
}
if intersects {
continue;
}
let xd = (points[i].x - points[j].x).abs() + 1;
let yd = (points[i].y - points[j].y).abs() + 1;
let area = xd * yd;
if area > max_area {
max_area = area;
}
}
}
max_area.to_string()
}
That’s a bit longer, isn’t it.
One point worth repeating is the comment:
All 4 vertices must be within the polygon
Because the polygons are on a grid of points, this means we can ignore the edge checks
This will skip rectangles with width/height = 1, but those won’t be max area (we assume)
Basically, the problem here is that the points we have are entire cells, so we’re going to be off by one on one side or the other. And what’s worse, we didn’t do that edge checking I was talking about. This lets us skip that: If a rectangle one smaller in each dimension is in the polygon, for this puzzle, that is good enough.
And it works!
$ just run-and-bench 9 part2
1572047142
part2: 117.595123ms ± 2.790635ms [min: 115.400375ms, max: 139.578917ms, median: 116.955541ms]
Quite a bit slower though.
One thing we can do is to move the area < max_area check above the polygon check. Once we’ve found the first valid rectangle, this will mean we can throw out the relatively expensive polygon contains checks.
$ just run-and-bench 9 part2_area_first
1572047142
part2_area_first: 75.403609ms ± 828.472µs [min: 74.197709ms, max: 82.072625ms, median: 75.324333ms]
Well. It is faster!
If I have time, I’ll come back and optimize that one. It really shouldn’t be that slow.
Visualization
So. What does this thing actually look like?
Well, to explain that, I added render_svg! and render_svg_frame! macros, the latter of which rasterizes each to a PNG before making a video. It takes a minute.
So what does our polygon look like?
That’s no moon.
Well. That explains a few things. 😄
It’s such a weird looking shape to do as a polygon…
If we animate our search:
Red rectangles aren’t in bounds. Yellow are, but are smaller than our current best. Light green is our current best and dark green marks finding new bests.
[12/13] Part 2 - Dimensional Compression
Combing back to this one, I had another idea. The points we’re working with are huge, so it’s hard to check if any given point is inside of the shape or not… but what if they weren’t?
Basically, we can convert each point. Instead of really large number, whatever the leftmost point in entire image is has x = 0, then the next will have x = 1, etc. Then, we can take that shape and flood fill to find the points inside of the shape. From that, for each pair of points, we actually can check every point in the rectangle to see if we have a valid area–using the original points to do the actual area calculation.
Something like this:
#[aoc::register]
fn part2_compress(input: &str) -> impl Into<String> {
let points = input.lines().map(Point2D::from).collect::<Vec<_>>();
let x_points = points.iter().map(|p| p.x).sorted().unique().collect::<Vec<_>>();
let y_points = points.iter().map(|p| p.y).sorted().unique().collect::<Vec<_>>();
let compressed_points = points
.iter()
.map(|p| {
Point2D::new(
x_points.iter().position(|&x| x == p.x).unwrap() as isize,
y_points.iter().position(|&y| y == p.y).unwrap() as isize,
)
})
.collect::<Vec<_>>();
#[derive(Debug, Copy, Clone, PartialEq, Eq)]
enum Cell {
Unknown,
Outside,
Inside,
Wall,
}
let mut grid = Grid::new(x_points.len() + 2, y_points.len() + 2, Cell::Unknown);
// Each point is a corner as are all points bewtween them
// This does assume that either x or y does not change
for (p1, p2) in compressed_points.iter().tuple_combinations() {
if p1.x == p2.x {
let x = p1.x + 1;
let y_start = p1.y.min(p2.y) + 1;
let y_end = p1.y.max(p2.y) + 1;
for y in y_start..=y_end {
grid.set(x, y, Cell::Wall);
}
} else if p1.y == p2.y {
let y = p1.y + 1;
let x_start = p1.x.min(p2.x) + 1;
let x_end = p1.x.max(p2.x) + 1;
for x in x_start..=x_end {
grid.set(x, y, Cell::Wall);
}
}
}
// Flood fill from (0,0) to mark outside
let mut stack = vec![(0isize, 0isize)];
while let Some((x, y)) = stack.pop() {
if grid.get(x, y) != Some(Cell::Unknown) {
continue;
}
grid.set(x, y, Cell::Outside);
for nx in (x - 1)..=(x + 1) {
for ny in (y - 1)..=(y + 1) {
if (nx == x || ny == y) && grid.get(nx, ny) == Some(Cell::Unknown) {
stack.push((nx, ny));
}
}
}
}
// Now any points that are still Unknown are Inside
for x in 0..grid.width() {
for y in 0..grid.height() {
if grid.get(x, y) == Some(Cell::Unknown) {
grid.set(x, y, Cell::Inside);
}
}
}
// For each pair of points, verify that all points in the rectangle are Inside or Wall
// Then calculate their area (uncompressed) and track the max
let mut max_area = 0;
for i in 0..compressed_points.len() {
for j in i + 1..compressed_points.len() {
let xd = (points[i].x - points[j].x).abs() + 1;
let yd = (points[i].y - points[j].y).abs() + 1;
let area = xd * yd;
if area <= max_area {
continue;
}
let x_start = compressed_points[i].x.min(compressed_points[j].x) + 1;
let x_end = compressed_points[i].x.max(compressed_points[j].x) + 1;
let y_start = compressed_points[i].y.min(compressed_points[j].y) + 1;
let y_end = compressed_points[i].y.max(compressed_points[j].y) + 1;
let mut valid = true;
'invalidate: for x in x_start..=x_end {
for y in y_start..=y_end {
match grid.get(x, y) {
Some(Cell::Inside) | Some(Cell::Wall) => {}
_ => {
valid = false;
break 'invalidate;
}
}
}
};
if !valid {
continue;
}
max_area = area;
}
}
max_area.to_string()
}
Which works!
$ just run-and-bench 9 part2_compress
1572047142
part2_compress: 30.645095ms ± 774.564µs [min: 29.709666ms, max: 37.695ms, median: 30.584916ms]
Here’s a rendering:
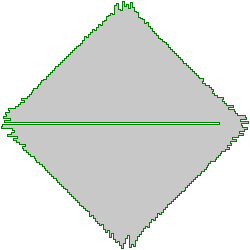
Not so circular any more, are you?! 😄
It’s fun/interesting that (even without really optimizing that code at all), it’s better than twice as fast as the intersection checks.
(It was ~45ms with the area check at the end, so that’s still a worthwhile optimization here.)
Benchmarks
$ just bench 9
part1: 113.22µs ± 5.711µs [min: 103.625µs, max: 145.292µs, median: 112.667µs]
part2: 117.772829ms ± 5.835355ms [min: 114.875834ms, max: 163.092666ms, median: 116.408125ms]
part2_area_first: 75.460115ms ± 4.87159ms [min: 73.968291ms, max: 122.868208ms, median: 74.794209ms]
part2_compress: 30.911492ms ± 348.699µs [min: 29.722667ms, max: 31.736125ms, median: 30.920791ms]
| Day | Part | Solution | Benchmark |
|---|---|---|---|
| 9 | 1 | part1 | 113.22µs ± 5.711µs |
| 9 | 2 | part2 | 117.772829ms ± 5.835355ms |
| 9 | 2 | part2_area_first | 75.460115ms ± 4.87159ms |
| 9 | 2 | part2_compress | 30.911492ms ± 348.699µs |