Source: Day 16: Reindeer Maze
Full solution for today (spoilers!).
Part 1
Given a maze, what is the shortest path between
SandEwhere walking straight costs one and turning costs 1000.
Okay, data structure and parsing:
#[derive(Debug, Clone)]
struct Puzzle {
start: Point,
end: Point,
walls: Grid<bool>,
}
#[aoc_generator(day16)]
pub fn parse(input: &str) -> Puzzle {
let walls = Grid::read(input, &|c| c == '#');
let newline_width = walls.width + 1;
let start = input.chars().position(&|c| c == 'S').unwrap();
let start = (start % newline_width, start / newline_width).into();
let end = input.chars().position(&|c| c == 'E').unwrap();
let end = (end % newline_width, end / newline_width).into();
Puzzle { start, end, walls }
}
First solution, let’s do a search with a priority queue. Keep the list sorted by how much time we’ve spent either going straight or apparently veeeerrrrryyy slowly turning in place. Once we get to the end, because of the priority.
#[aoc(day16, part1, pq)]
fn part1_pq(input: &Puzzle) -> usize {
let mut pq = PriorityQueue::new();
pq.push((input.start, Direction::Right), 0_isize);
let mut checked = HashSet::new();
while let Some(((point, direction), cost)) = pq.pop() {
if point == input.end {
return (-cost) as usize;
}
if !checked.insert((point, direction)) {
continue;
}
// Walk straight
let new_point = point + direction;
if input.walls.get(new_point) != Some(&true) {
pq.push((new_point, direction), cost - 1);
}
// Turn left or right
// Optimize slightly by only queueing a turn if there's no wall
// TODO: This might fail on the starting condition?
let new_d = direction.rotate_left();
if input.walls.get(point + new_d) != Some(&true) {
pq.push((point, new_d), cost - 1000);
}
let new_d = direction.rotate_right();
if input.walls.get(point + new_d) != Some(&true) {
pq.push((point, new_d), cost - 1000);
}
}
// If we've made it here, the maze is unsolvable
// Or we wrote something wrong :smile:
panic!("unsolvable maze");
}
Not much code after all.
$ cargo aoc --day 16 --part 1
AOC 2024
Day 16 - Part 1 - pq : 65436
generator: 51.083µs,
runner: 2.630333ms
Not bad. And I can make a fun video watching the order it searches in (skipping frames, because it’s entirely too long otherwise):
Optimization 1: A*
Okay, fine. I wrote it my myself. Let’s go ahead and throw A* at it. 😄
#[aoc(day16, part1, astar)]
fn part1_astar(input: &Puzzle) -> i32 {
match pathfinding::prelude::astar(
&(input.start, Direction::Right),
|(point, direction)| {
let mut successors = vec![];
// Walk straight
let new_point = *point + *direction;
if input.walls.get(new_point) != Some(&true) {
successors.push(((new_point, *direction), 1));
}
// Turn left or right
// Optimize slightly by only queueing a turn if there's no wall
let new_direction = direction.rotate_left();
if input.walls.get(*point + new_direction) != Some(&true) {
successors.push(((*point, new_direction), 1000));
}
let new_direction = direction.rotate_right();
if input.walls.get(*point + new_direction) != Some(&true) {
successors.push(((*point, new_direction), 1000));
}
successors
},
|(point, _)| point.manhattan_distance(&input.end),
|(point, _)| *point == input.end,
) {
Some((_, cost)) => cost,
_ => panic!("unsolvable maze"),
}
}
Mostly, we have to define the successor function. I do thrown in a bit of a heuristic (Manhattan distance to the exit), but given how expensive turns are, I don’t think it helps that much.
And … it’s a bit quicker?
$ cargo aoc --day 16 --part 1
AOC 2024
Day 16 - Part 1 - pq : 65436
generator: 51.083µs,
runner: 2.630333ms
Day 16 - Part 1 - astar : 65436
generator: 53.167µs,
runner: 1.924ms
I think the difference is easier to see in a video:
And here are both, side by side (priority queue on the left, a* on the right):
Part 2
There are multiple ‘shortest’ paths; how many unique points are there in all of those paths.
It did try to extend my algorithm with the priority queue from part 1, but the problem is that we can’t use the same ‘duplicate work detection’ algorithm, since you specifically want to hit the same point multiple times.
On the other hand, it turns out that moving to the pathfinding crate makes this kind of trivial, just use astar_bag, which returns all of the fastest solutions:
#[aoc(day16, part2, astar)]
fn part2_astar(input: &Puzzle) -> usize {
match pathfinding::prelude::astar_bag(
&(input.start, Direction::Right),
|(point, direction)| {
let mut successors = vec![];
// Walk straight
let new_point = *point + *direction;
if input.walls.get(new_point) != Some(&true) {
successors.push(((new_point, *direction), 1));
}
// Turn left or right
// Optimize slightly by only queueing a turn if there's no wall
let new_direction = direction.rotate_left();
if input.walls.get(*point + new_direction) != Some(&true) {
successors.push(((*point, new_direction), 1000));
}
let new_direction = direction.rotate_right();
if input.walls.get(*point + new_direction) != Some(&true) {
successors.push(((*point, new_direction), 1000));
}
successors
},
|(point, _)| point.manhattan_distance(&input.end),
|(point, _)| *point == input.end,
) {
Some((solutions, _)) => {
let mut all_best_points = HashSet::new();
for solution in solutions {
for (point, _) in solution {
all_best_points.insert(point);
}
}
all_best_points.len()
}
_ => panic!("unsolvable maze"),
}
}
$ cargo aoc --day 16 --part 2
AOC 2024
Day 16 - Part 2 - astar : 489
generator: 45.542µs,
runner: 3.787166ms
Still over a ms, but it’s fast enough for today.
I expect if I wanted to optimize this even more, I’d want to remove all of the nodes between any two points except for branching points. Save a lot on the recursion. I actually worked on this for a while, but the dramatic cost for turning makes that a bit more complicated. So it goes.
In case you were curious, here are what all the points (for my input) look like:
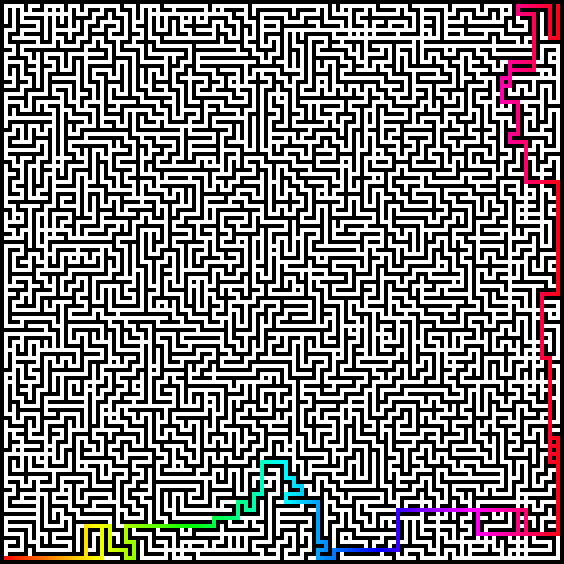
A few tiny branches, that’s all.
Benchmarks
cargo aoc bench --day 16
Day16 - Part1/pq time: [2.7459 ms 2.7979 ms 2.8631 ms]
Day16 - Part1/astar time: [1.6206 ms 1.6368 ms 1.6622 ms]
Day16 - Part2/astar time: [3.5064 ms 3.5274 ms 3.5525 ms]
Onward!