Source: Day 14: Restroom Redoubt
Full solution for today (spoilers!).
Part 1
Given a series of robots defined with initial
positionandvelocityon a 101x103 toroidal grid, calculate where the robots will be after 100 iterations. Return the product of the number of robots in each quadrant of the final grid, ignoring the middle lines (since they’re odd).
I think the quadrant calculations are actually going to be the hardest part of that.
First, the parsing:
#[derive(Debug, Clone, Copy, PartialEq, Eq)]
struct Robot {
position: Point,
velocity: Point,
}
#[aoc_generator(day14)]
fn parse(input: &str) -> (usize, usize, Vec<Robot>) {
let mut width = 101;
let mut height = 103;
let mut robots = vec![];
for line in input.lines() {
if line.is_empty() {
continue;
}
if line.starts_with("#") {
let (w, h) = line[2..].split_once("x").unwrap();
width = w.parse().unwrap();
height = h.parse().unwrap();
continue;
}
let (point, velocity) = line.split_once(" ").unwrap();
let (px, py) = point[2..].split_once(",").unwrap();
let (vx, vy) = velocity[2..].split_once(",").unwrap();
robots.push(Robot {
position: (px.parse::<i32>().unwrap(), py.parse::<i32>().unwrap()).into(),
velocity: (vx.parse::<i32>().unwrap(), vy.parse::<i32>().unwrap()).into(),
})
}
(width, height, robots)
}
Now, we can run the simulation very quickly:
#[aoc(day14, part1, v1)]
fn part1_v1((width, height, input): &(usize, usize, Vec<Robot>)) -> usize {
let mut robots = input.clone();
for _i in 0..100 {
for robot in robots.iter_mut() {
robot.position += robot.velocity;
robot.position.x = robot.position.x.rem_euclid(*width as i32);
robot.position.y = robot.position.y.rem_euclid(*height as i32);
}
}
// TODO: quadrant stuff
}
But like I said:
#[aoc(day14, part1, v1)]
fn part1_v1((width, height, input): &(usize, usize, Vec<Robot>)) -> usize {
let mut robots = input.clone();
for _i in 0..100 {
for robot in robots.iter_mut() {
robot.position += robot.velocity;
robot.position.x = robot.position.x.rem_euclid(*width as i32);
robot.position.y = robot.position.y.rem_euclid(*height as i32);
}
}
let mut quadrant_scores = [0; 4];
let half_width_left = *width as i32 / 2;
let half_height_left = *height as i32 / 2;
// The bottom/right quadrants do not include the middle row if the height/width is odd
let half_height_right = if height % 2 == 1 {
half_height_left + 1
} else {
half_height_left
};
let half_width_right = if width % 2 == 1 {
half_width_left + 1
} else {
half_width_left
};
for robot in robots.iter() {
if robot.position.x < half_width_left && robot.position.y < half_height_left {
quadrant_scores[0] += 1;
} else if robot.position.x >= half_width_right && robot.position.y < half_height_left {
quadrant_scores[1] += 1;
} else if robot.position.x < half_width_left && robot.position.y >= half_height_right {
quadrant_scores[2] += 1;
} else if robot.position.x >= half_width_right && robot.position.y >= half_height_right {
quadrant_scores[3] += 1;
}
// Any other robots are on a line
}
quadrant_scores.iter().product::<usize>()
}
That would be much shorter if I just hard coded all the sizes, but at least in this case, the example problem is significantly smaller, so I keep it flexible.
Here’s a rendering if you want to watch it:
There are a couple of interesting ‘stutters’ in that image. We’ll come back to that…
Part 2
Find the first time the robots come together in the shape of a christmas tree.
Wat.

It’s chaos.
I have no idea what it’s eventually supposed to look like. I originally assumed it would be the entire image and symmetrical (so we could calculate it with quadrants 0 and 1 being equal as well as 2 and 3), but that’s not actually the case.
The easiest way to deal with this one I think is just to render out each frame and go looking…
fn render(width: usize, height: usize, robots: &[Robot], path: &str) {
println!("Rendering frame: {path}...");
let mut image = ImageBuffer::new(width as u32, height as u32);
// Render any point that is a robot
for robot in robots.iter() {
image.put_pixel(
robot.position.x as u32,
robot.position.y as u32,
image::Rgb([255_u8, 255_u8, 255_u8]),
);
}
let image = imageops::resize(
&image,
width as u32 * 4,
height as u32 * 4,
image::imageops::Nearest,
);
image.save(path).unwrap();
}
And just dump the frames until one is interesting!

Well, that’s one way to solve the problem!
But how in the world do we automate it?
First try, I now know what the output image looks like. There’s a 30x32 box with a christmas tree inside of it. So let’s just detect that box and see if that is enough:
#[aoc(day14, part2, v1)]
fn part2_v1((width, height, input): &(usize, usize, Vec<Robot>)) -> usize {
if *width != 101 || *height != 103 {
return 0; // this doesn't work for the example case
}
let mut robots = input.clone();
// Advance each robot until the image magically appears
let mut timer = 0;
loop {
timer += 1;
for robot in robots.iter_mut() {
robot.position += robot.velocity;
robot.position.x = robot.position.x.rem_euclid(*width as i32);
robot.position.y = robot.position.y.rem_euclid(*height as i32);
}
// Target image is 31x33 with a 1x border
// Let's try just detecting the border
let mut grid: Grid<bool> = Grid::new(*width, *height);
for robot in robots.iter() {
*grid.get_mut(robot.position).unwrap() = true;
}
let mut border_found = true;
'border_patrol: for start_x in 0..*width {
'next_point: for start_y in 0..*height {
for xd in 0..31 {
if grid.get((start_x + xd, start_y)) != Some(&true) {
border_found = false;
continue 'next_point;
}
if grid.get((start_x + xd, start_y + 32)) != Some(&true) {
border_found = false;
continue 'next_point;
}
}
for yd in 0..33 {
if grid.get((start_x, start_y + yd)) != Some(&true) {
border_found = false;
continue 'next_point;
}
if grid.get((start_x + 30, start_y + yd)) != Some(&true) {
border_found = false;
continue 'next_point;
}
}
border_found = true;
break 'border_patrol;
}
}
if border_found {
return timer;
}
assert!(
timer < 100_000,
"Did not find symmetric image in 100_000 iterations"
);
}
}
That is a bit ugly, but in effect the entire inner loop, for each iteration, goes through each point, looking for a solid outline of pixels exactly 30x32 in size.
It works for my input at least!
$ cargo aoc --day 14 --part 2
AOC 2024
Day 14 - Part 2 - v1 : 8053
generator: 53.791µs,
runner: 93.395084ms
I think I can do better though. Especially trying to avoid creating and populating a grid each iteration.
Optimization 1: Weird shape detection
Okay, looking through the output images (and based on the stutters in part 1), I also noticed that there are some ‘strange’ inputs:
Frame 19

Frame 74

Frame 122

Frame 175
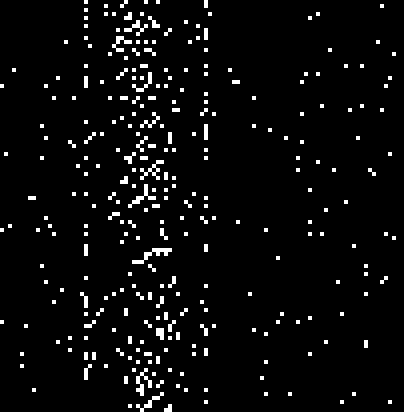
Frame 225
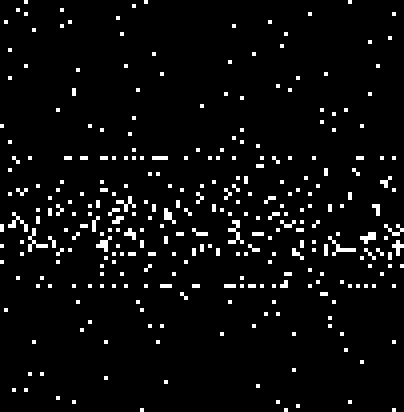
Frame 276
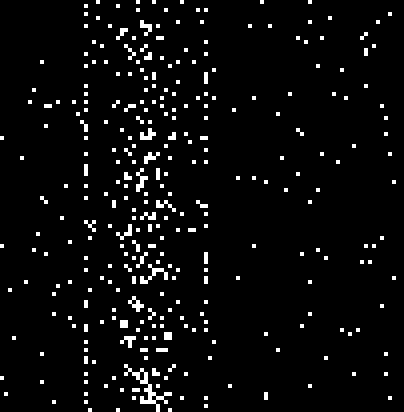
Looking at those, we have a pair of repeating ‘patterns’ of all the bots mostly being in the right row/column every 101/103 iterations (which, of course, are are width and height of the simulation).
We then know (for our case):
$$ 19 + 103t_1 = target \\ 74 + 101t_2 = target $$
For some $t_1$ and $t_2$. It’s not quite equal though, in my case it’s 78 and 79. That’s because (I think) the actual zero for the second one was before we started, so they’re off by one cycle.
In any case:
#[aoc(day14, part2, v2)]
fn part2_v2((width, height, input): &(usize, usize, Vec<Robot>)) -> usize {
if *width != 101 || *height != 103 {
return 0; // this doesn't work for the example case
}
let mut robots = input.clone();
let mut hline_start = None;
let mut vline_start = None;
// Advance each robot until the image magically appears
let mut timer = 0;
loop {
timer += 1;
for robot in robots.iter_mut() {
robot.position += robot.velocity;
robot.position.x = robot.position.x.rem_euclid(*width as i32);
robot.position.y = robot.position.y.rem_euclid(*height as i32);
}
// Check for unusually many 'busy' horizontal lines
if hline_start.is_none() {
let mut hline_counts: Vec<usize> = vec![0; *height];
for robot in robots.iter() {
hline_counts[robot.position.y as usize] += 1;
}
if hline_counts.iter().filter(|v| **v > 20).count() > 3 {
hline_start = Some(timer);
}
}
// Check for unusually many 'busy' vertical lines
if vline_start.is_none() {
let mut vline_counts: Vec<usize> = vec![0; *width];
for robot in robots.iter() {
vline_counts[robot.position.x as usize] += 1;
}
if vline_counts.iter().filter(|v| **v > 20).count() > 3 {
vline_start = Some(timer);
}
}
// If we have both, we have an answer
// I'm still not sure why the cycles can be off by ±1
// NOTE: This is incorrect, see the correction below
if hline_start.is_some() && vline_start.is_some() {
for h_times in 0..100 {
for v_times in (h_times - 1)..=(h_times + 1) {
if hline_start.unwrap() + 103 * h_times == vline_start.unwrap() + 101 * v_times
{
return hline_start.unwrap() + 103 * h_times;
}
}
}
unreachable!();
}
assert!(
timer < 10_000,
"Did not find symmetric image in 100_000 iterations"
);
}
}
That is some pretty bonkers code. Especially the htimes ± 1 mess. But it returns the right answer!
Edit: Nope. It doesn’t. See here.
And it’s substantially quicker:
$ cargo aoc --day 14 --part 2
AOC 2024
Day 14 - Part 2 - v1 : 8053
generator: 53.791µs,
runner: 93.395084ms
Day 14 - Part 2 - v2 : 8053
generator: 60.583µs,
runner: 69.208µs
A 1000x speedup? We’ll take that!
Correction for Optimization 1: Chinese Remainder Theorem
It turns out… that whole ‘off by one’ I was trying to account for was actually just a feature of my input. Many others’ inputs had a different of 2 or more. So that’s not at all how you’re supposed to solve the problem.
Instead, you have two sets of cycles, which you can use the Chinese Remainder Theorem to solve:
// If we have both, we have an answer
// I'm still not sure why the cycles can be off by ±1
if hline_start.is_some() && vline_start.is_some() {
// Solve using the Chinese remainder theorem
let h_offset = hline_start.unwrap() % *height;
let v_offset = vline_start.unwrap() % *width;
let mut h_timer = h_offset;
let mut v_timer = v_offset;
loop {
if h_timer == v_timer {
return h_timer;
}
if h_timer < v_timer {
h_timer += *height;
} else {
v_timer += *width;
}
}
}
Check out the wikipedia page above for more details on how/why exactly works, but the nice thing is that it doesn’t have to iterate through to find this value, instead it iterates down both at once.
In the end, the runtime is the same and it has the advantage of actually being correct on more than my input.
Woot!
Benchmarks
cargo aoc bench --day 14
Day14 - Part1/v1 time: [61.077 µs 61.951 µs 63.315 µs]
Day14 - Part2/v1 time: [95.193 ms 96.097 ms 97.173 ms]
Day14 - Part2/v2 time: [65.454 µs 65.853 µs 66.328 µs]
Pretty cool.
Onward!