Source: Day 11: Plutonian Pebbles
Full solution for today (spoilers!).
Part 1
Given a sequence of values
v_n, replace each value with the first matching rule:
if v = 0 -> 1- If
vhas an even number of digits, split it (sov = 8675becomes[86, 75])- Otherwise,
v -> v * 2024Calculate how many elements are in the sequence after 25 iterations.
Seems straight forward enough:
#[aoc_generator(day11)]
fn parse(input: &str) -> Vec<u64> {
input.split_ascii_whitespace().map(|l| l.parse().unwrap()).collect()
}
fn blink(input: &[u64], count: usize) -> usize {
let mut input = input.iter().copied().collect::<Vec<_>>();
for _i in 0..count {
input = input.iter().flat_map(|&v| {
if v == 0 {
vec![1]
} else {
let digit_count = v.ilog10() as u32 + 1;
if digit_count % 2 == 0 {
let divisor = 10u64.pow(digit_count / 2);
vec![v / divisor, v % divisor]
} else {
vec![v * 2024]
}
}
}).collect();
}
input.iter().count()
}
#[aoc(day11, part1, v1)]
fn part1_v1(input: &[u64]) -> usize {
blink(input, 25)
}
And it works fine:
$ cargo aoc --day 11 --part 1
AOC 2024
Day 11 - Part 1 - v1 : 194482
generator: 334ns,
runner: 11.658833ms
On to go, right?
Optimization 1: Recursion
Well… that’s not going to scale. And I can guarantee (having already finished the day) that we’re going to have to solve a much bigger number of blinks next time.
The main drawback we have right now is that we’re keeping the entire (up to 200k element long) vector around, making a new copy and moving a ton of values each time. That cannot be efficient.
Trick is, we don’t need to do that! We actually only care what the length is. And even better, there’s no interaction between the subset of the vector from one sequence to another (once we’ve split the vector with the second case, we never join to either neighbor).
This is a perfect case for recursion!
// Solve it recursively instead
fn blink_recur(input: &[u64], count: usize) -> usize {
fn recur(value: u64, depth: usize) -> usize {
if depth == 0 {
1
} else if value == 0 {
recur(1, depth - 1)
} else {
let digit_count = value.ilog10() as u32 + 1;
if digit_count % 2 == 0 {
let divisor = 10u64.pow(digit_count / 2);
recur(value / divisor, depth - 1) + recur(value % divisor, depth - 1)
} else {
recur(value * 2024, depth - 1)
}
}
}
input.iter().map(|&v| recur(v, count)).sum::<usize>()
}
#[aoc(day11, part1, recursive)]
fn part1_recursive(input: &[u64]) -> usize {
blink_recur(input, 25)
}
That’s actually pretty elegant, so long as you’re used to recursion. We’re guaranteed a base case (once we reach depth = count, we have a length of 1 element) and each recursive case is making progress (depth = depth - 1), so we’re good to go:
$ cargo aoc --day 11 --part 1
AOC 2024
Day 11 - Part 1 - v1 : 194482
generator: 334ns,
runner: 11.658833ms
Day 11 - Part 1 - recursive : 194482
generator: 625ns,
runner: 1.169375ms
Nice!
Optimization 2: Memoization
But we can do better.
My guess is that we’re going to duplicate a lot of work as we’re going. If one branch of this giant recursion finds that we have N steps after we see a 0 with 15 steps to go… well, that will always be true!
So we’re going to create a cache of (value, depth) -> steps. Now, whenever we recur, if we’ve already recorded the value for any given value, just return it (cutting out all of the substeps!); otherwise, calculate it and cache it!
// Add memoization
fn blink_recur_memo(input: &[u64], count: usize) -> usize {
fn recur(cache: &mut HashMap<(u64, usize), usize>, value: u64, depth: usize) -> usize {
if let Some(&v) = cache.get(&(value, depth)) {
return v
}
let result = if depth == 0 {
1
} else if value == 0 {
recur(cache, 1, depth - 1)
} else {
let digit_count = value.ilog10() as u32 + 1;
if digit_count % 2 == 0 {
let divisor = 10u64.pow(digit_count / 2);
recur(cache, value / divisor, depth - 1) + recur(cache, value % divisor, depth - 1)
} else {
recur(cache, value * 2024, depth - 1)
}
};
cache.insert((value, depth), result);
result
}
let mut cache = HashMap::new();
input.iter().map(|&v| recur(&mut cache, v, count)).sum::<usize>()
}
#[aoc(day11, part1, recursive_memo)]
fn part1_recursive_memo(input: &[u64]) -> usize {
blink_recur_memo(input, 25)
}
And man, we get a nice speedup for that one:
$ cargo aoc --day 11 --part 1
AOC 2024
Day 11 - Part 1 - v1 : 194482
generator: 334ns,
runner: 11.658833ms
Day 11 - Part 1 - recursive : 194482
generator: 625ns,
runner: 1.169375ms
Day 11 - Part 1 - recursive_memo : 194482
generator: 250ns,
runner: 171.375µs
Part 2
Run the simulation for 75 steps.
Told you. 😄
#[aoc(day11, part2, recursive_memo)]
fn part2_recursive_memo(input: &[u64]) -> usize {
blink_recur_memo(input, 75)
}
And here we go:
$ cargo aoc --day 11 --part 2
AOC 2024
Day 11 - Part 2 - recursive_memo : 232454623677743
generator: 709ns,
runner: 4.954ms
Out of curiosity, I (started) to run the direct solution on part 2:
$ cargo aoc --day 11 --part 2
Day 11 - Part 2 - recursive_memo : 232454623677743
generator: 750ns,
runner: 7.680458ms
[Blink 0, 0.00]: 8
[Blink 1, 0.00]: 11
[Blink 2, 0.00]: 15
[Blink 3, 0.00]: 22
[Blink 4, 0.00]: 35
[Blink 5, 0.00]: 46
...
[Blink 45, 36.76]: 831739064
[Blink 46, 56.00]: 1264009436
[Blink 47, 85.29]: 1920832260
[Blink 48, 129.54]: 2914729482
[Blink 49, 200.84]: 4431170168
[Blink 50, 313.49]: 6727602136
[Blink 51, 485.09]: 10218016566
...
We’re already over 8 minutes at only 51 with a clearly exponential growth curve:
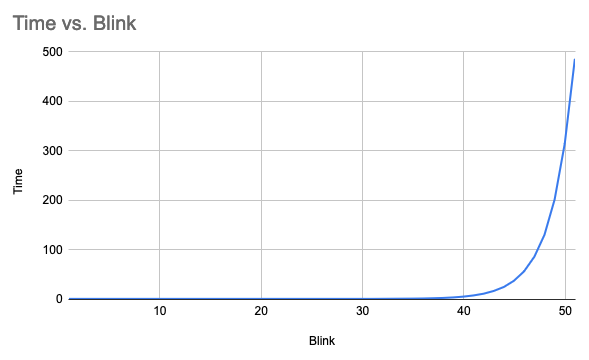
And here’s the recursive version without memoization:
$ cargo aoc --day 11 --part 2
AOC 2024
[Blink 0, 0.00]: 8
[Blink 1, 0.00]: 11
[Blink 2, 0.00]: 15
[Blink 3, 0.00]: 22
[Blink 4, 0.00]: 35
[Blink 5, 0.00]: 46
...
[Blink 45, 4.57]: 831739064
[Blink 46, 6.99]: 1264009436
[Blink 47, 10.75]: 1920832260
[Blink 48, 16.17]: 2914729482
[Blink 49, 24.70]: 4431170168
[Blink 50, 37.64]: 6727602136
[Blink 51, 57.47]: 10218016566
...
Much better, but still exponential:
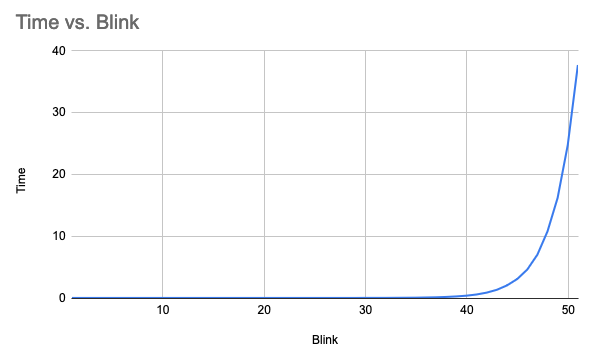
And with ~1/3 of the problem to go!
So… we’ll stick to the memoized version. 😄
Optimization (attempt) 3: Association list cache
Out of curiosity, I wondered if using an association list for the cache instead of a hashmap would help any:
fn blink_recur_memo_assoc(input: &[u64], count: usize) -> usize {
fn recur(cache: &mut Vec<(u64, usize, usize)>, value: u64, depth: usize) -> usize {
if let Some(r) = cache
.iter()
.find_map(|(v, d, r)| {
if *v == value && *d == depth {
Some(*r)
} else {
None
}
})
{
return r;
}
// ...
cache.push((value, depth, result));
result
}
let mut cache = vec![];
input
.iter()
.map(|&v| recur(&mut cache, v, count))
.sum::<usize>()
}
Unfortunately, not really. In this case, the O(n) constants from re-allocating and scanning the Vec outweigh the O(1) constants of hashing.
$ cargo aoc --day 11 --part 2
AOC 2024
Day 11 - Part 2 - recursive_memo : 232454623677743
generator: 11.875µs,
runner: 4.933167ms
Day 11 - Part 2 - recursive_memo_assoc : 232454623677743
generator: 875ns,
runner: 3.543555083s
Optimization (attempt) 4: BTree cache
What about a BTree?
In this case, really all you have to do is replace the HashMap with BTreeMap. This should give us O(log n), but what about the constants?
$ cargo aoc --day 11 --part 2
AOC 2024
Day 11 - Part 2 - recursive_memo : 232454623677743
generator: 11.875µs,
runner: 4.933167ms
Day 11 - Part 2 - recursive_memo_assoc : 232454623677743
generator: 875ns,
runner: 3.543555083s
Day 11 - Part 2 - recursive_memo_btree : 232454623677743
generator: 2µs,
runner: 28.405458ms
That’s pretty close! But not quite there. So it goes.
Optimization 5: Iterate over HashMap<value, count>
Okay, one last optimization, this time we’re going to ignore all of the fancy recursion and memoization and iterate directly. But rather than storing the entire vector, we’re going to use the fact that the order does not matter at all and instead just keep a count of how many times we see each value:
fn blink_count_hash(input: &[u64], count: usize) -> usize {
let mut list1 = HashMap::new();
let mut list2 = HashMap::new();
for v in input {
list1.entry(*v).and_modify(|c| *c += 1).or_insert(1);
}
for _ in 0..count {
for (v, c) in list1.drain() {
if v == 0 {
list2.entry(1).and_modify(|c2| *c2 += c).or_insert(c);
} else {
let digit_count = v.ilog10() + 1;
if digit_count % 2 == 0 {
let divisor = 10u64.pow(digit_count / 2);
list2
.entry(v / divisor)
.and_modify(|c2| *c2 += c)
.or_insert(c);
list2
.entry(v % divisor)
.and_modify(|c2| *c2 += c)
.or_insert(c);
} else {
list2.entry(v * 2024).and_modify(|c2| *c2 += c).or_insert(c);
}
}
}
std::mem::swap(&mut list1, &mut list2);
list2.clear();
}
list1.values().sum()
}
Even with clearing one list each time (so we don’t re-alloc), it’s still a bit quicker:
$ $ cargo aoc --day 11
AOC 2024
Day 11 - Part 2 - recursive_memo : 232454623677743
generator: 11.875µs,
runner: 4.933167ms
Day 11 - Part 1 - count_hash : 194482
generator: 459ns,
runner: 92.916µs
Day 11 - Part 2 - recursive_memo : 232454623677743
generator: 11.875µs,
runner: 4.933167ms
Day 11 - Part 2 - count_hash : 232454623677743
generator: 1.125µs,
runner: 2.748583ms
Benchmarks
$ cargo aoc bench --day 11
Day11 - Part1/v1 time: [8.4353 ms 8.4996 ms 8.6118 ms]
Day11 - Part1/recursive time: [1.0363 ms 1.0448 ms 1.0569 ms]
Day11 - Part1/recursive_memo time: [112.83 µs 113.84 µs 115.80 µs]
Day11 - Part1/count_hash time: [84.005 µs 84.317 µs 84.666 µs]
Day11 - Part2/recursive_memo time: [4.4928 ms 4.5440 ms 4.6099 ms]
Day11 - Part2/recursive_memo_assoc time: [3.6567 s 3.6678 s 3.6792 s]
Day11 - Part2/recursive_memo_btree time: [28.396 ms 28.763 ms 29.323 ms]
Day11 - Part2/count_hash time: [2.7752 ms 2.7868 ms 2.7996 ms]