Another day (week? month?), another puzzle game.
This time around, we’re going to solve Golf Peaks. I picked this up a while ago on iOS, but only recently on Steam. It’s a cute little puzzle game themed around minigolf.
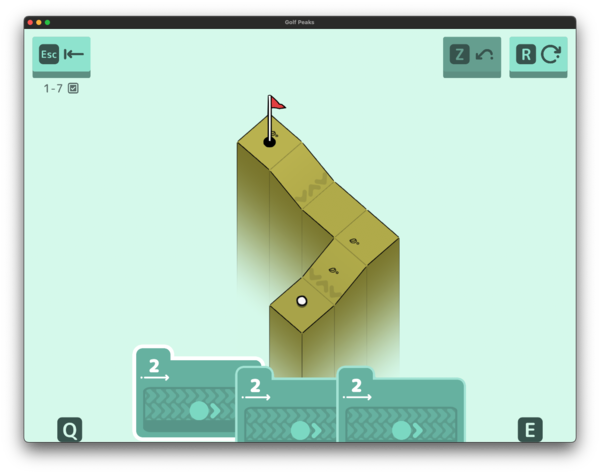
Basically, you’re on a grid and you have to get the ball (in the bottom in that screenshot above) to the flag (currently at the top). You have a set list of moves you can take, styled as cards–all of which either move a certain number of tiles in a specific direction or possibly jump into the air (and fly over obstacles).
It gets more complicated from there, but hopefully you have the basic idea. 😄
The initial/basic model
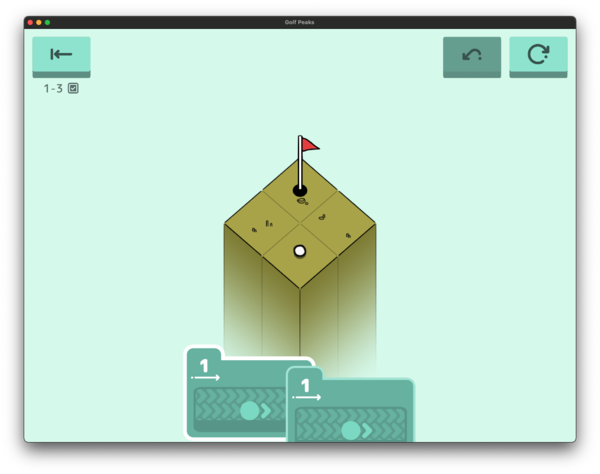
Okay, to start out with, we’re going to represent Tiles as an enum (since I’m writing this after finishing the game, I know we’ll have a bunch 😄).
#[derive(Debug, Clone, Copy, PartialEq, Eq, Hash)]
enum Tile {
Empty,
Flat(usize),
...
}
The map (our Global state) will then hold all of the tiles, the location of the flag, and any solutions (for test cases later):
#[derive(Debug, Clone)]
struct Global {
width: usize,
height: usize,
tiles: Vec<Tile>,
flag: Point,
solutions: Vec<String>,
}
Then the Local state should store any Cards remaining (they look like cards, so that’s what I’ve called them throughout) plus the current location of the ball:
#[derive(Debug, Clone, Copy, PartialEq, Eq, Hash)]
enum Card {
Move(usize),
Jump(usize),
}
#[derive(Debug, Clone, Hash, PartialEq, Eq)]
struct Local {
ball: Point,
cards: Vec<Card>,
}
This is eventually going to have to change (eventually we’ll add moves that Jump and then Move), but for the first good number of puzzles this will work.
And finally, our Step will be a Card in a Direction:
#[derive(Debug, Clone, Copy, PartialEq, Eq, Hash)]
struct Step {
card: Card,
direction: Direction,
}
We do also need a function to read in the initial Global + Local state, but I’m not going to get into that much detail here. Suffice it to say… it got complicated…
9x9
0,flag 5,left 3 2,*e 0 1,left 2,left 3,warp0 x
5,up 4,warp0 3 2,*e 0,ice 1,left 2,left 3,/bl 3,warp1
3 3 3,ice 2,*e 0 1,left 1,icetr 2,down 2,down
2,*s 2,*s 2,*s 2,ice 2,*e 2,*s 1,down 1,down 1,down
0 0,ice 0 2,*s 1,ball 2,*e 0 0,ice 0,ice
1,up 1,up 1,up 2,*e 2,*s 2 1,up 1,up 1,up
2,up 2,up 1,icebl 1,right 0 1,left 1 2,*w 2,*n
2 3,warp2 2,right 1,right 0,ice 1,left 2,*n 3,/tl 3,warp1
x 2 2,right 1 0,ice 1 2,*w 3,warp2 x
1- 1- 2- 2- 1/ 1/ 1/1- 1/1- 1/2-
1/↗ 2-↙ 1/1-↙ 1-↖ 1/2-↖ 1/1-↗ 1-↗ 2-↖ 1/↗
(We’ll get to all of those different kinds of tiles later.)
😄
Generating states
Okay, the next step for a solver is to impelement State::next_states. At first, it’s relatively clean:
impl State<Global, Step> for Local {
fn next_states(&self, global: &Global) -> Option<Vec<(i64, Step, Self)>>
where
Self: Sized {
let mut next_states = Vec::new();
for (i, card) in self.cards.iter().enumerate() {
for direction in Direction::all() {
let mut next_state = self.clone();
next_state.cards.remove(i);
if !match card {
Card::Move(strength) => next_state.try_move(global, direction, *strength),
Card::Jump(strength) => next_state.try_jump(global, direction, *strength),
} {
// Invalid state, try next direction
continue;
}
next_states.push((1, Step { card: *card, direction }, next_state));
}
}
if next_states.is_empty() {
return None;
}
Some(next_states)
}
}
As we’ve done in several of these posts now, we go through each possible move (each Card in each Direction) and queue up each of those as a state. Currently, we just handle everything in a try_move and try_jump function on the Local. Each of those is designed to return bool if the move/jump ‘worked’. If it returns false (currently, if the ball falls off the map), then that state isn’t considered as part of a solution.
try_move
So how do we try_move?
impl Local {
fn try_move(&mut self, global: &Global, direction: Direction, strength: usize) -> bool {
// No more moving to do, we're done
if strength == 0 {
return true;
}
let current_height = match global.tile_at(self.ball) {
Tile::Empty => unreachable!(),
Tile::Flat(height) => height,
};
let next_point = self.ball + Point::from(direction);
let next_tile = global.tile_at(next_point);
// Trying to move into empty space/out of bounds
if let Tile::Empty = next_tile {
return false;
}
// Normal flat tile
if let Tile::Flat(height) = next_tile {
// On the same level, just move
if height == current_height {
self.ball = next_point;
return self.try_move(global, direction, strength - 1);
}
// New tile is higher, bounce
// This effectively reverses direction and moves 'back' to the same tile
if height > current_height {
return self.try_move(global, direction.flip(), strength - 1);
}
// New tile is lower, fall?
if height < current_height {
todo!()
}
unreachable!();
}
// Normal flat tile, recur
self.ball = self.ball + direction.into();
self.try_move(global, direction, strength - 1)
}
}
We certainly have some room for expansion, since I knew even then we’d be adding in a bunch of different kinds of tiles.
try_jump
Jumping… is much easier.
impl Local {
fn try_jump(&mut self, global: &Global, direction: Direction, strength: usize) -> bool {
let next_point = self.ball + Point::from(direction) * strength as isize;
let next_tile = global.tile_at(next_point);
// Trying to jump into empty space
if let Tile::Empty = next_tile {
return false;
}
// Otherwise, it always works
self.ball = next_point;
true
}
}
Jumping explicitly just ignores any intervening terrain (there’s not a ‘jump height’), so we just teleport. Whee!
And that’s all we need to solve all of the levels up until ~1.7 when slopes are introduced!
Sloped tiles

Okay, first addition will be sloped tiles. These will come back a number of times as we interact with other kinds of tiles, but the basic idea is this:
- If you are moving ‘with’ the slope (either up or down),
try_movewill treat it as flat and end up going up/down a level - If you end a move or jump on a slope, you will slide down the slope (possibly in a chain)
There’s one (major) edge case here that actually doesn’t come up until 9-6 (falling sideways onto slopes).
Slopes will be handled as Tile::Slope(usize, Direction) where the first is the height of the top of the slope and the Direction is ‘down’ the slope.
try_move has a few updates. First, we calculate the current height a bit differently for slopes:
let current_height = match global.tile_at(self.ball) {
Tile::Empty => unreachable!(),
Tile::Flat(height) => height,
Tile::Slope(height, slope_direction) => if direction == slope_direction {
height
} else if direction == slope_direction.flip() {
height - 1
} else {
return false; // TODO: Support this?
},
};
That TODO: Support this? is the side on case I mentioned earlier. It doesn’t come up for a surprisingly long time. Other than that, the height of the slope is as specified in the map at the top and one less at the bottom.
Then, later moving onto a slope:
if let Tile::Slope(height, slope_direction) = next_tile {
// Sliding down at the proper height
if height == current_height && (slope_direction == direction || slope_direction == direction.flip()) {
self.ball = next_point;
return self.try_move(global, direction, strength - 1);
}
// Dropping down onto a slope
if height < current_height {
self.ball = next_point;
return self.try_move(global, direction, strength - 1);
}
// Anything else we don't support for now
// TODO: Support this?
return false;
}
And that’s it for try_move, but we do need to add on a try_slopes function:
fn try_slopes(&mut self, global: &Global) -> bool {
let current_tile = global.tile_at(self.ball);
if current_tile == Tile::Empty {
return false;
}
// Slopes apply a single tile move than recur
if let Tile::Slope(_, slope_direction) = current_tile {
if !self.try_move(global, slope_direction, 1) {
return false;
}
return self.try_slopes(global);
}
// Any non-slopes just don't slide
true
}
What this is going to do is, after each move, if you’re currently on a Slope, use try_move to move once on that slope (which will check bouncing into something or falling off the level) and then try_slope again in case there are multiple ones in a chain.
To implement this, our next_states becomes this:
// ...
for (i, card) in self.cards.iter().enumerate() {
for direction in Direction::all() {
let mut next_state = self.clone();
next_state.cards.remove(i);
if !match card {
Card::Move(strength) => next_state.try_move(global, direction, *strength),
Card::Jump(strength) => next_state.try_jump(global, direction, *strength),
} {
// Invalid state, try next direction
continue;
}
// Apply slopes
next_state.try_slopes(global);
next_states.push((1, Step { card: *card, direction }, next_state));
}
}
// ...
Pretty good for now!
Multiple step moves
Whelp. It was good while it lasted. It turns out that our current implementation of Cards isn’t sufficient, we need to be able play a single card that can Jump and Move in the same direction (and there are a number of things that end up applying in between those two states).
Now, instead of a single card, we’re going to implement a Card that can have 1 or more CardSteps:
enum CardStep {
Move(usize),
Jump(usize),
None,
}
const CARD_MAX_STEPS: usize = 10;
#[derive(Debug, Clone, Copy, PartialEq, Eq, Hash)]
struct Card([CardStep;CARD_MAX_STEPS]);
I use a constant array with size 10 here (I eventually drop this to 3) because you can’t get Copy if you’re going to store them in a Vec<CardStep>. Copy has to be constant size and inline (no pointers). Technically, I really didn’t have to do this. I expected that we might end up with even more interesting moves or cards as we want (perhaps ones that turn in midair? or 3+ steps?) but… this is as complicated as we get. We’ll never do anything other than Move(usize), Jump(usize), or JumpAndMove(usize, usize).
But it was still fun to implement! 😄
And the actual implementation is not at all that bad:
for (i, card) in self.cards.iter().enumerate() {
for direction in Direction::all() {
let mut next_state = self.clone();
next_state.cards.remove(i);
for card_step in card.0.iter() {
let step_success = match card_step {
CardStep::Move(strength) => next_state.try_move(global, direction, *strength),
CardStep::Jump(strength) => next_state.try_jump(global, direction, *strength),
CardStep::None => break,
};
if !step_success {
// Invalid state, try next direction
continue;
}
// Apply slopes
next_state.try_slopes(global);
}
next_states.push((1, Step { card: *card, direction }, next_state));
}
}
We still loop over each Card in each Direction, but now when actually implementing the move, we apply each step in turn, failing if after any one of them we end up off the board.
One interesting bug I did have in the initial implementation was that I only applied slopes at the end. But apparently, you can apply them in between the Jump and the Move (already fixed above).
While I was working on this, I did end up pulling in the ‘solution checker’ that I wrote about in Solving Sokobond. Each level file will also include any possible solutions I’ve found for that level. That lets me write a single test case that will try all solved levels and make sure we still generate a valid solution even after I change things. Go go gadget integration tests!
Bouncing off angled walls
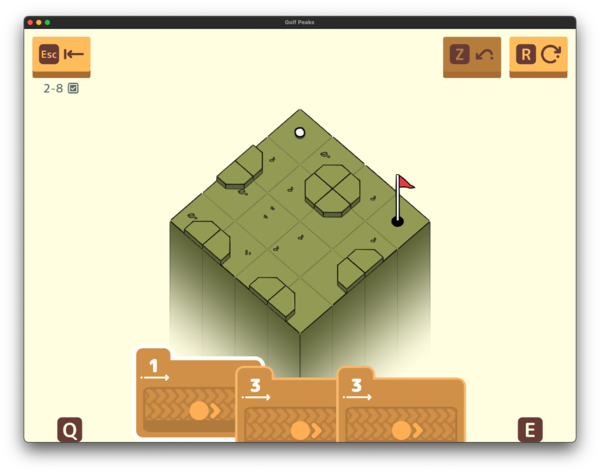
Okay, still in world 2, we do have one more trick. This time we have angled walls. If a ball comes in from either of the sides with the angled wall, it will change direction. The other two basically act as walls one step higher.
To implement this, first I’m going to define an enum to store the four possible AngleTypes:
#[derive(Debug, Clone, Copy, PartialEq, Eq, Hash)]
enum AngleType {
TopLeft,
TopRight,
BottomLeft,
BottomRight,
}
impl AngleType {
fn try_reflect(&self, direction: Direction) -> Option<Direction> {
match self {
AngleType::TopLeft => match direction {
Direction::Up => Some(Direction::Right),
Direction::Left => Some(Direction::Down),
_ => None,
},
AngleType::TopRight => match direction {
Direction::Up => Some(Direction::Left),
Direction::Right => Some(Direction::Down),
_ => None,
},
AngleType::BottomLeft => match direction {
Direction::Down => Some(Direction::Right),
Direction::Left => Some(Direction::Up),
_ => None,
},
AngleType::BottomRight => match direction {
Direction::Down => Some(Direction::Left),
Direction::Right => Some(Direction::Up),
_ => None,
},
}
}
}
#[derive(Debug, Clone, Copy, PartialEq, Eq, Hash)]
enum Tile {
Empty,
Flat(usize),
Slope(usize, Direction),
Angle(usize, AngleType),
}
I originally had these stored using a pair of Direction, but … it got confusing, mostly because I didn’t have the two ordered. This is much better.
To handle this in try_move, we end up adding a new block after Tile::Slope but before the base ‘flat’ case:
impl Local {
fn try_move(&mut self, global: &Global, direction: Direction, strength: usize) -> bool {
// ...
// Angled tiles
// On either of their angled sides, reflect to the other
// On the other two, treat them as a wall
if let Tile::Angle(height, a_type) = next_tile {
// If we're on the same height and reflect
if height == current_height {
if let Some(new_direction) = a_type.try_reflect(direction) {
self.ball = next_point;
return self.try_move(global, new_direction, strength - 1);
}
}
// Otherwise, always treat this as a wall one height (fall through)
next_tile = Tile::Flat(height + 1);
}
// ...
}
}
If we bounce off the angle, we’ll recur on try_move in the new direction and immediately return it’s response, this will handle the bounce. But the interesting part is that we can modify next_tile here (which doesn’t modify the Global map, since it’s intentionally immutable) and fall through to treat it as a flat tile if you bounce into the ‘back’ of it.
And that’s it. Angles!
Sand
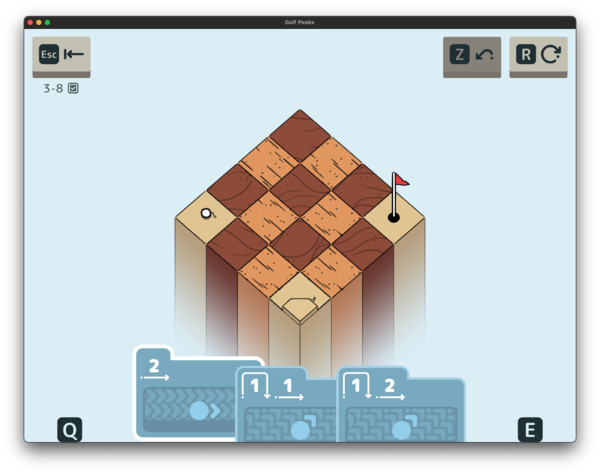
World 3’s trick? Sand! Also quicksand. This is 3-8, which has both of them.
#[derive(Debug, Clone, Copy, PartialEq, Eq, Hash)]
enum Tile {
Empty,
Flat(usize),
Slope(usize, Direction),
Angle(usize, AngleType),
Sand(usize),
}
impl Local {
fn try_move(&mut self, global: &Global, direction: Direction, strength: usize) -> bool {
// ...
// Cannot slide out of sand, just stop moving
// But return true, this isn't an error, just stopping
if let Tile::Sand(_) = current_tile {
return true;
}
// ...
}
}
Instead of recurring try_move with strength - 1… we just immediately return true. And that’s enough to stop the ball in it’s tracks when it try_moves across sand.
I like the easy ones.
Quicksand
Quicksand though, that one is slightly more sneaky.
- As long as you are moving,
Quicksandis treated as a normal flat tile - If you finish a card on quicksand, the ball slowly sinks (which should return
falsefromtry_move)
#[derive(Debug, Clone, Copy, PartialEq, Eq, Hash)]
enum Tile {
Empty,
Flat(usize),
Slope(usize, Direction),
Angle(usize, AngleType),
Sand(usize),
Quicksand(usize),
}
To actually implement this properly, I did do a bit of refactoring. Rather than next_states handling the different kinds of cards itself, I instead created a new try_card function on Local which will properly handle a single Card in a single Direction:
- For each step of the
CardMove/Jumpas specified- Check for slopes
- After each step is done, check
Quicksand
Something like this:
impl Local {
fn try_card(&mut self, global: &Global, card: Card, direction: Direction) -> bool {
for card_step in card.0.iter() {
let success = match card_step {
CardStep::Move(strength) => self.try_move(global, direction, *strength),
CardStep::Jump(strength) => self.try_jump(global, direction, *strength),
CardStep::None => break,
};
if !success {
return false;
}
if !self.try_slopes(global) {
return false;
}
}
// On quicksand, we fail
if let Tile::Quicksand(_) = global.tile_at(self.ball) {
return false;
}
true
}
}
Now the next_states loop just becomes:
for (i, card) in self.cards.iter().enumerate() {
'next_direction: for direction in Direction::all() {
let mut next_state = self.clone();
next_state.cards.remove(i);
if !next_state.try_card(global, *card, direction) {
// Invalid state, try next direction
continue 'next_direction;
}
next_states.push((1, Step { card: *card, direction }, next_state));
}
}
If I had this in more than one file, this would be pub fn try_card and try_move / try_jump / etc would all be private so I can force myself only to call this one. As it is though… well I just have to be careful, now don’t I? 😄
Water
Next up, world 4 and water traps!

Water is interesting, since it wouldn’t make any sense to immediately lose the level (you could just leave it open). Instead, if a ball ever falls into water, it will respawn–not where you hit the ball from, but rather on the last ‘safe’ tile that the ball moved across. So you can respawn on Flat or Sand, but not Slope or Quicksand. (Technically Angle is allowed as well.)
#[derive(Debug, Clone, Copy, PartialEq, Eq, Hash)]
enum Tile {
Empty,
Flat(usize),
Slope(usize, Direction),
Angle(usize, AngleType),
Sand(usize),
Quicksand(usize),
Water(usize),
}
#[derive(Debug, Clone, Hash, PartialEq, Eq)]
struct Local {
ball: Point,
cards: Vec<Card>,
last_safe: Point,
}
This requires a few changes. In try_card, if we end a move on water (this can be between steps as well), revert to the last_safe point:
impl Local {
fn try_card(&mut self, global: &Global, card: Card, direction: Direction) -> bool {
for card_step in card.0.iter() {
let success = match card_step {
CardStep::Move(strength) => self.try_move(global, direction, *strength),
CardStep::Jump(strength) => self.try_jump(global, direction, *strength),
CardStep::None => break,
};
if !success {
return false;
}
// If after any step, we're on water, reset to last safe tile and stop move
// This shouldn't apply after move (it's handled in try_move), but might after jump or slide
if let Tile::Water(_) = global.tile_at(self.ball) {
self.ball = self.last_safe;
return true;
}
}
// ...
}
}
Then, when we try_move, if we’re moving from a safe tile, we can mark it + handle falling into water during a move (jump and slide are handled above):
impl Local {
fn try_move(&mut self, global: &Global, direction: Direction, strength: usize) -> bool {
let current_tile = global.tile_at(self.ball);
// If we're on a flat/safe tile, mark this as the last safe spot
if let Tile::Flat(_) | Tile::Angle(_, _) | Tile::Sand(_) = current_tile {
self.last_safe = self.ball;
}
// ...
// Trying to move onto water, fall back to last safe tile and end move
if let Tile::Water(_) = next_tile {
self.ball = self.last_safe;
return true;
}
// Normal flat tile, recur
self.ball = self.ball + direction.into();
self.try_move(global, direction, strength - 1)
}
}
It’s interesting that try_move succeeds if the ball falls in water, but that’s actually what a lot of levels in this section are built around, which is kind of cool.
Springs
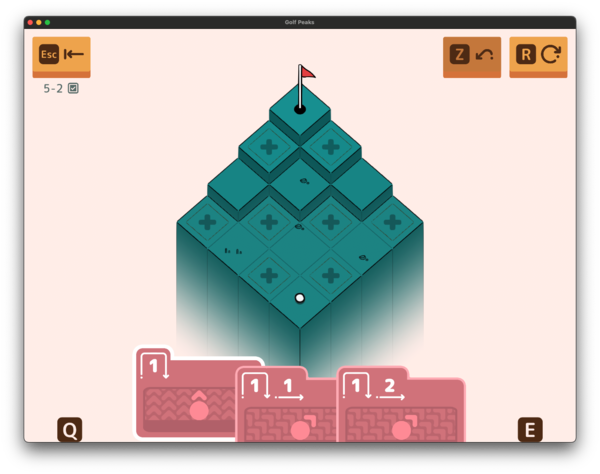
Next up, world 5 is built around springs. Basically if you hit a spring part of the way through a Move, treat it as a Jump for the rest of the move.
#[derive(Debug, Clone, Copy, PartialEq, Eq, Hash)]
enum Tile {
Empty,
Flat(usize),
Slope(usize, Direction),
Angle(usize, AngleType),
Sand(usize),
Quicksand(usize),
Water(usize),
Spring(usize),
}
impl Local {
fn try_card(&mut self, global: &Global, card: Card, direction: Direction) -> bool {
let mut bouncing = false;
for card_step in card.0.iter() {
let success = match card_step {
CardStep::Move(strength) => if bouncing {
self.try_jump(global, direction, *strength)
} else {
self.try_move(global, direction, *strength)
},
CardStep::Jump(strength) => self.try_jump(global, direction, *strength),
CardStep::None => break,
};
if !success {
return false;
}
// ...
// If we end part of a card on a spring, the next move counts as a jump
if let Tile::Spring(_) = global.tile_at(self.ball) {
bouncing = true;
}
}
// ...
}
fn try_move(&mut self, global: &Global, direction: Direction, strength: usize) -> bool {
// ...
// If we move onto a spring, treat the rest of the move as a jump
if let Tile::Spring(_) = next_tile {
self.ball = self.ball + direction.into();
return self.try_jump(global, direction, strength - 1);
}
// Normal flat tile, recur
self.ball = self.ball + direction.into();
self.try_move(global, direction, strength - 1)
}
}
For try_move, the change is easy enough. If we see a Spring, call to try_jump for the next part of the move instead of try_move. But we also need to handle an interesting edge case. If you have a Jump(1) + Move(1) card and after the jump you end up on a Spring, then the Move part needs to be handled as a Jump instead. Which of course comes up in levels in this section. Whee!
Warps / Teleporters
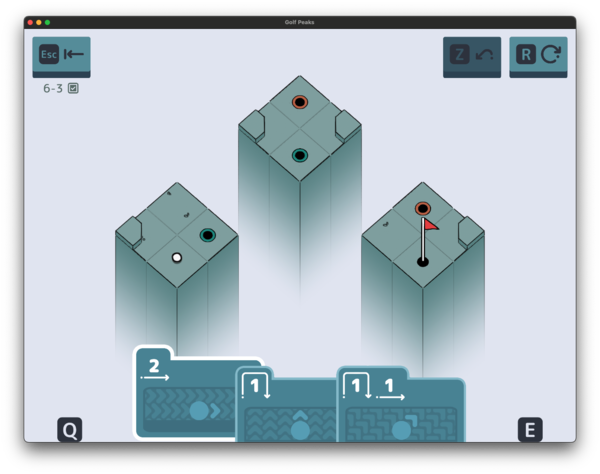
Up next, warps! Or teleporters. Or holes, although in golf that would be the flag, so I had to rename them. 😄
#[derive(Debug, Clone, Copy, PartialEq, Eq, Hash)]
enum Tile {
Empty,
Flat(usize),
Slope(usize, Direction),
Angle(usize, AngleType),
Sand(usize),
Quicksand(usize),
Water(usize),
Spring(usize),
Warp(usize, usize),
}
The extra second parameter here is the id of the Warp since (as you can see in the above picture), it’s possible to have multiple pairs of Warps per level–although you’ll always have exactly a pair of each kind (no non-determinism here thankfully).
I originally had this inline with the try_card functionality, but you can also actually see it in the middle of a try_slope, so I had to refactor again.
On thing that’s interesting is this one does not at all touch try_move or try_jump, since you cannot warp in the middle of a CardStep.
impl Local {
fn try_card(&mut self, global: &Global, card: Card, direction: Direction) -> bool {
// ...
for card_step in card.0.iter() {
// ...
self.try_warp(global);
// If we end on the flag, we don't have to finish this card
if self.ball == global.flag {
return true;
}
}
// ...
}
fn try_slopes(&mut self, global: &Global) -> bool {
let current_tile = global.tile_at(self.ball);
if current_tile == Tile::Empty {
return false;
}
// Slopes apply a single tile move than recur
if let Tile::Slope(_, slope_direction) = current_tile {
if !self.try_move(global, slope_direction, 1) {
return false;
}
self.try_warp(global);
return self.try_slopes(global);
}
// Any non-slopes just don't slide
true
}
fn try_warp(&mut self, global: &Global) {
// If we're on a warp after any card part, transport to the other half
if let Tile::Warp(_, warp_index) = global.tile_at(self.ball) {
let ball_index = self.ball.y as usize * global.width + self.ball.x as usize;
let other_warp_map_index = global
.tiles
.iter()
.enumerate()
.find_map(|(other_index, tile)| {
if other_index == ball_index {
None
} else if let Tile::Warp(_, other_warp_index) = tile {
if *other_warp_index == warp_index {
return Some(other_index);
} else {
None
}
} else {
None
}
})
.expect("No other warp in map");
self.ball = Point {
x: (other_warp_map_index % global.width) as isize,
y: (other_warp_map_index / global.width) as isize,
};
}
}
}
I probably could have directly stored the ‘warp to’ point in the Tile::Warp on load (which I’m just thinking about now), but I didn’t really have any performance problems with this as is, so it’s fine to leave for now.
The worst warp level
So remember how I said that we only ever have pairs of warps?
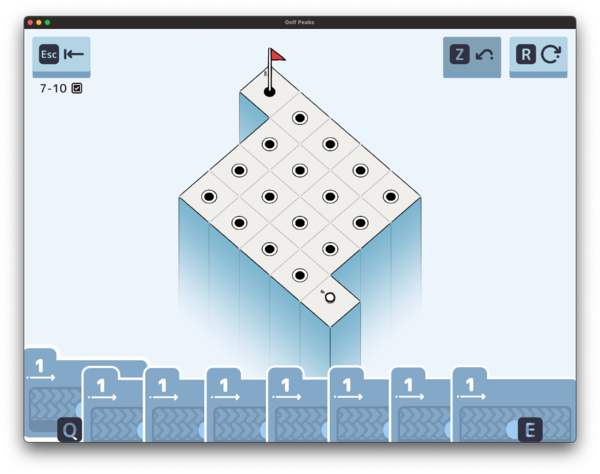
Yeah… that was a surprising level to see 😄
Technically, each one is still only part of a single pair, but there’s no visual indicator. You instead have to manually go through each to figure out where they all go.
6x4
0,flag 0,warp7 0,warp6 0,warp4 0,warp7 x
x 0,warp1 0,warp0 0,warp5 0,warp3 x
x 0,warp2 0,warp1 0,warp6 0,warp2 x
x 0,warp4 0,warp3 0,warp5 0,warp0 0,ball
1- 1- 1- 1- 1- 1- 1- 1-
1-↖ 1-↘ 1-↖ 1-↗ 1-
1-↖ 1-↘ 1-↖ 1-↗ 1-↖
Interesting. Annoying to code for the solver. But interesting.
Belts
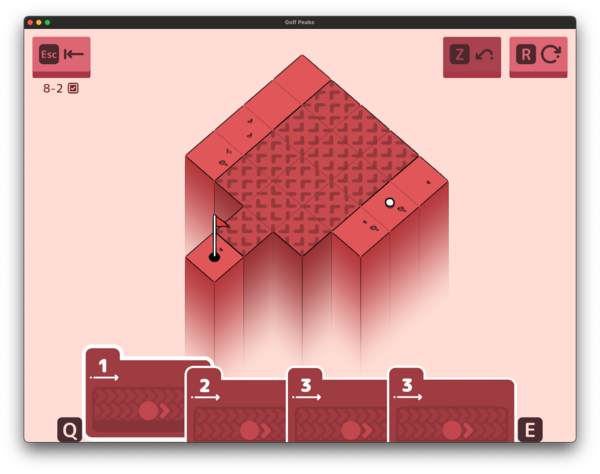
So… these are a bit weird. They really are slopes that are flat. There’s not actually an edge case that I ever found where they’d be treated differently. Which makes them (implementation wise) easier than slopes, since you don’t have to deal with falling onto them from the sides or the high/low side.
impl Local {
fn try_slopes(&mut self, global: &Global) -> bool {
let current_tile = global.tile_at(self.ball);
if current_tile == Tile::Empty {
return false;
}
// Slopes apply a single tile move than recur
if let Tile::Slope(_, slope_direction) = current_tile {
if !self.try_move(global, slope_direction, 1) {
return false;
}
self.try_warp(global);
return self.try_slopes(global);
}
// Same for belts
if let Tile::Belt(_, belt_direction) = current_tile {
if !self.try_move(global, belt_direction, 1) {
return false;
}
self.try_warp(global);
return self.try_slopes(global);
}
// Any non-slopes just don't slide
true
}
}
That’s… really it. I could actually have rewritten this in arguably a more compact syntax:
impl Local {
fn try_slopes(&mut self, global: &Global) -> bool {
let current_tile = global.tile_at(self.ball);
if current_tile == Tile::Empty {
return false;
}
// Slopes and belts apply a single tile move than recur
match current_tile {
Tile::Slope(_, direction) | Tile::Belt(_, direction) => {
if !self.try_move(global, direction, 1) {
return false;
}
self.try_warp(global);
return self.try_slopes(global);
},
_ => {}
}
// Any non-slopes just don't slide
true
}
}
I just … didn’t think about it until I saw the code when writing this post. Oops. 😄
Edge case: Falling sideways onto slopes

Ooh ice. Ice is nice.
So this is an interesting one. Ice will basically work in that if you finish a Card on ice, you will continue to move in the same direction until either:
- You move off the
Iceonto some other kind ofTile - You ‘bounce’ into a wall, staying on the same
Iceblock
This ended up being a bit tricky to implement though, since the direction you’re moving can change mid-move (Angles), but the Ice won’t be implemented until try_card. So we either need to return the last direction … or store it in the Local state. Let’s go with the latter:
It gets even more complicated (but also even more fun) when you introduce Ice + Angles:
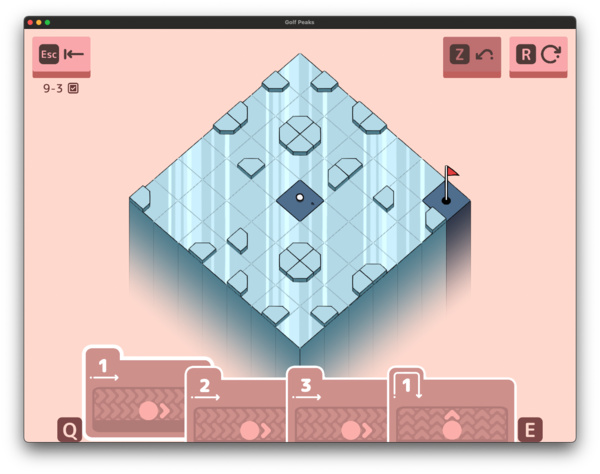
I could have implemented this as a single spot on the map having multiple Tile attributes, but instead, I just made this IceAngle.
#[derive(Debug, Clone, Hash, PartialEq, Eq)]
struct Local {
ball: Point,
cards: Vec<Card>,
last_safe: Point,
last_move: Direction,
}
Now unlike last_safe, we do need to set last_move on things like Slope, so we end up setting it a bunch of different places. This was by far the most interesting single addition (pair of additions?) to the game.
I ended up implementing this with last_move as above (should that have been slide_direction?) + refactoring the try_slope method into try_slide instead, which will handle Slopes, Belts, and now Ice.
impl Local {
fn try_card(&mut self, global: &Global, card: Card, direction: Direction) -> bool {
let mut direction = direction;
let mut bouncing = false;
for card_step in card.0.iter() {
// ...
}
if !self.try_slide(global) {
return false;
}
// On quicksand, we fail
if let Tile::Quicksand(_) = global.tile_at(self.ball) {
return false;
}
true
}
fn try_slide(&mut self, global: &Global) -> bool {
let current_tile = global.tile_at(self.ball);
if current_tile == Tile::Empty {
return false;
}
// ...
// If we're on ice, continue to slide in that direction until it changes
loop {
match global.tile_at(self.ball) {
Tile::Ice(_) | Tile::IceAngle(_, _) => {}
_ => break,
}
let start_position = self.ball;
let success = self.try_move(global, self.last_move, 1);
// Fell off the map (most likely)
if !success {
return false;
}
// Didn't actually slide, probably bounced
if self.ball == start_position {
break;
}
}
// Any non-slopes just don't slide
true
}
}
Sideways slope fix
This… was not the end of these levels though. We also ended up having to fix a really old bug.
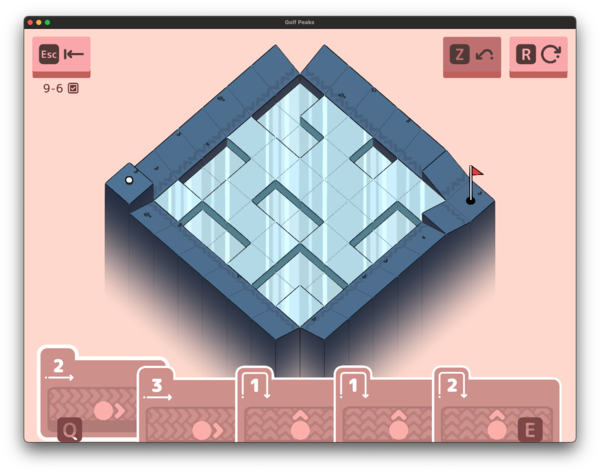
It turns out that if you fall onto a Slope from above, it immediately cancels your momentum and you slide down it. This is really the only difference between Belts and Slopes (other than the height difference).
It took a while to find this one…
Loops
And finally, we’re on to the last levels.
For the most part, there was nothing new here, just a culmination of all of the tricks of the other 9 worlds. We did finally (in 10.5) come across our first loop though:

See it yet?
It’s down in the bottom left, with the two IceAngles forming one end of a rectangle with the Belts along one side.
This was interesting to fix. Essentially, I added a loop detection cache to Local (which has to be Clone, but not Copy, so we can use a Vec!)
#[derive(Debug, Clone, Hash, PartialEq, Eq)]
struct Local {
ball: Point,
cards: Vec<Card>,
last_safe: Point,
last_move: Direction,
slide_loop_cache: Vec<(Point, Direction)>,
}
This is reset in try_card and then only used in try_slide:
impl Local {
fn try_card(&mut self, global: &Global, card: Card, direction: Direction) -> bool {
let mut direction = direction;
log::debug!("try_card({:?}, {card:?}, {direction:?})", self.ball);
// Keep a cache of moves we've seen on the same card while sliding
// If we see the same move again, we're in a loop and should stop
self.slide_loop_cache.clear();
// ...
if !self.try_slide(global) {
return false;
}
// ...
}
fn try_slide(&mut self, global: &Global) -> bool {
if global.tile_at(self.ball) == Tile::Empty {
return false;
}
fn is_ice(tile: Tile) -> bool {
match tile {
Tile::Ice(_) | Tile::IceAngle(_, _) => true,
_ => false,
}
}
// If we're on ice, continue to slide in that direction until it changes
// This is if + while to deal with the warp at the end of ice case
if is_ice(global.tile_at(self.ball)) {
// Keep sliding until we hit something that isn't ice
while is_ice(global.tile_at(self.ball)) {
// Update/check slide loop check
if self.slide_loop_cache.contains(&(self.ball, self.last_move)) {
return false;
}
self.slide_loop_cache.push((self.ball, self.last_move));
let start_position = self.ball;
let success = self.try_move(global, self.last_move, 1);
// Fell off the map (most likely)
if !success {
return false;
}
// Didn't actually slide, probably bounced
if self.ball == start_position {
break;
}
}
self.try_warp(global);
}
// Slopes apply a single tile move than recur
if let Tile::Slope(_, slope_direction) = global.tile_at(self.ball) {
// Update/check slide loop check
if self.slide_loop_cache.contains(&(self.ball, slope_direction)) {
return false;
}
self.slide_loop_cache.push((self.ball, slope_direction));
// Try to slide down the slope
if !self.try_move(global, slope_direction, 1) {
return false;
}
self.try_warp(global);
return self.try_slide(global);
}
// Same for belts
if let Tile::Belt(_, belt_direction) = global.tile_at(self.ball) {
// Update/check slide loop check
if self.slide_loop_cache.contains(&(self.ball, belt_direction)) {
return false;
}
self.slide_loop_cache.push((self.ball, belt_direction));
// Try to get pushed by the belt
if !self.try_move(global, belt_direction, 1) {
return false;
}
self.try_warp(global);
return self.try_slide(global);
}
// Any non-slopes just don't slide
true
}
}
Yes, I know, I still have both Tile::Slope and Tile::Belt with identical code. But otherwise, it’s easy. Each time we slide, store the ball location and direction in the cache. If we ever see the same as something in the cache, we have a loop, so this isn’t a valid solution.
Oops!
It works well though.
The final level
And so we come to the end.

This is a fun one. Except… where in the world is the flag?!
Fin.
And that’s it! There’s a hidden 19th Hole in the credits , but that’s it.
That was a fun game. It was kind of nice to work on a solver for something with such a ridiculously smaller exploration space. In this case, there’s a maximum of (4n)!
(where n is the number of cards) possible moves.
The most cards is 9 in 10-12 (the last level!). Which… is technically 3.71e41 states… but a vast majority of those are invalid (jumping off the level or not doing anything interesting). To find the solution, I only ended up having to evaluate 6831 of those states, which was the most states of any of the puzzles here (there wasn’t one with fewer cards but a higher branching factor).
Even that took less about half a second on my laptop in debug mode. In release mode, it took 0.05 seconds. So I really wasn’t worried about optimization for this one. 😄