We’ve gone through all sorts of things building up the StackLang language so far:
Posts in StackLang:
But what can we actually do with it?
Nothing that particularly deep (yet), but I did think the code for generating the Mandelbrot set is pretty cool!
Full source code for StackLang: github:jpverkamp/stacklang
Factorial (in three parts)
Factorial - calculating the product of 1 to N.
It’s a great first problem to implement, mostly because you can do it at least two ways (with a loop or recursively). Other than that, it’s simple math: add and multiply.
So let’s try to write out the solution a few different ways!
With a loop
First up, a loop. In StackLang, the loop syntax is { @block } @iter loop. Assuming @iter is a number N times, { @block } will be called N times, with each of those values being sent as the last parameter.
So we can directly calculate 10 fact as so:
1 # Push the initial 1 onto the stack
{ @2 1 + * } # The loop block:
# - Take two parameters (the current value and the loop index) and return 1 (the default)
# - Add 1 to the loop index (it's zero based)
# - Multiply and 'return' that value for the next iteration
10 # The value of N
loop # Call the loop
Or in a single line: 1 { @2 1 + * } 10 loop. It’s a bit esoteric, not going to lie, but I do like how compact it can be!
As a function
Okay, but what if we want to generalize? Perhaps even (le gasp) call it more than once?
Well, that’s easy enough. We can take the above, wrap it up in a new block all it’s own (taking one named parameter @n), and name it @fact:
{
@n
1 { @2 1 + * } n loop
} @fact
Now we just call it:
10 fact writeln
Pretty cool.
With recursion
Okay, we can do it with loops, what about recursion? To make this work:
- Take a value N
- If N is 1, return 1 (this is the base case)
- If not, calculate
fact(N - 1)(recursion!) and multiply by N (the recursive case)
It translates pretty directly to StackLang:
{
@n
1 # True case
{ @0 n 1 - fact n * } # False case
n 1 < if # Check if n < 1 (<= would be the same if one step faster)
} @fact
That’s it! From the outside, 10 fact works exactly the same as the loop based function.
Fibonacci
On to Fibonacci. This falls into mostly the same category as Factorial. It’s a simple math definition that’s great for testing code.
In this case, fib(0) = fib(1) = 1 and fib(n) = fib(n-1) + fib(n-2).
Or non-recursively, start with the list 1 1. Until you reach N (+1) elements, generate a new element by adding the current last two numbers. So 1 1 -> 1 1 2 -> 1 1 2 3 -> 1 1 2 3 5.
Naive recursion
First, let’s just implement it (naively) with the recursive definition:
Naive
{
@[n]
1
{
@0 !1
n 1 - fib
n 2 - fib
+
}
n 2 <= if
} @fib
It’s much the same as the recursive factorial function. Have a base case (n 2 <= that returns 1), otherwise have a block. In this case, it takes no parameters and returns 1 (@0 !1), calculates fib(n - 1) and fib(n - 2) and adds them.
That’s it!
But there’s one problem with that. Let’s expand fib(3):
Not so bad. 7 nodes. What about fib(5)?
Already 15 nodes.
As you might expect, it increases very very quickly. Each time, roughly doubling the number of nodes. So how long does it take (with this code, even compiled) to calculate fib(50)?
$ cargo run --release -- --file examples/fibonacci-naive-block.stack --compile > output/fibonacci-naive-block.c
Finished release [optimized] target(s) in 0.09s
Running `target/release/stacklang --file examples/fibonacci-naive-block.stack --compile`
$ clang -Ofast output/fibonacci-naive-block.c -o output/fibonacci-naive-block
$ time output/fibonacci-naive-block
102334155
real 0m12.347s
user 0m11.571s
sys 0m0.060s
That should not take that long.
But there’s good news! That’s an awful of lot of duplicated work. Just how many times are we calculating fib(2) after all?
With a loop
The much faster way to solve the problem is to build from the ground up. Make that list (implicitly), adding two numbers until we get the final form. You can do this two ways: with a loop and recursively with a helper function.
First, with a loop:
{
@n
1 1
{
@1 !1 # pop n (ignore it), return a+b
@[a b n] # name the top three values of the stack a, b, n
a b + # push a + b
}
n 2 - loop
} @fib
40 fib write
It’s a bit funny looking, but essentially we’re going to keep the entire list on the stack. Start by pushing the two initial 1s (and that’s why there’s an n 2 - at the end).
Then loop to fill out the list. Each time, we pop a single value (@1) which we’re going to ignore. That’s the loop index. Then we peek/name the top three values of the stack: @[a b n]. We could also start the loop block with @[a b n], but that implies that we want to pop those three values off the stack, which we do not. Finally, pop the new sum and continue.
After the loop has run, the stack should contain the fibonacci sequence all the way up to N. We can see this in debug mode:
$ cargo run -- --debug --file examples/fibonacci-loop.stack --compile > output/fibonacci-loop.c
Compiling stacklang v0.1.0 (/Users/jp/Projects/stacklang)
Finished dev [unoptimized + debuginfo] target(s) in 1.26s
Running `target/debug/stacklang --debug --file examples/fibonacci-loop.stack --compile`
$ clang output/fibonacci-loop.c -o output/fibonacci-loop
$ output/fibonacci-loop
[DEBUG] block_0 called -- STACK: <empty>
[DEBUG] block_1 called -- STACK: 40 {block} NAMES: fib={block}
[DEBUG] block_2 called -- STACK: 0 1 1 40 {block} NAMES: n=40 | fib={block}
[DEBUG] block_2 return -- STACK: 2 1 1 40 {block} NAMES: n=2 b=1 a=1 n=40 | fib={block}
[DEBUG] block_2 called -- STACK: 1 2 1 1 40 {block} NAMES: n=40 | fib={block}
[DEBUG] block_2 return -- STACK: 3 2 1 1 40 {block} NAMES: n=3 b=2 a=1 n=40 | fib={block}
[DEBUG] block_2 called -- STACK: 2 3 2 1 1 40 {block} NAMES: n=40 | fib={block}
[DEBUG] block_2 return -- STACK: 5 3 2 1 1 40 {block} NAMES: n=5 b=3 a=2 n=40 | fib={block}
[DEBUG] block_2 called -- STACK: 3 5 3 2 1 1 40 {block} NAMES: n=40 | fib={block}
[DEBUG] block_2 return -- STACK: 8 5 3 2 1 1 40 {block} NAMES: n=8 b=5 a=3 n=40 | fib={block}
[DEBUG] block_2 called -- STACK: 4 8 5 3 2 1 1 40 {block} NAMES: n=40 | fib={block}
[DEBUG] block_2 return -- STACK: 13 8 5 3 2 1 1 40 {block} NAMES: n=13 b=8 a=5 n=40 | fib={block}
...
That’s pretty cool to see!
Running it for the original 40:
$ cargo run --release -- --file examples/fibonacci-loop.stack --compile > output/fibonacci-loop.c
Finished release [optimized] target(s) in 0.11s
Running `target/release/stacklang --file examples/fibonacci-loop.stack --compile`
$ clang -Ofast output/fibonacci-loop.c -o output/fibonacci-loop
$ time output/fibonacci-loop
102334155
real 0m0.085s
user 0m0.001s
sys 0m0.001s
Pretty cool. Much much faster.
Loop, only keeping two
But it turns out… why are we actually keeping the entire stack? We never actually need anything other than the most recent two values. So rather than the trick to name/peek, let’s actually go ahead and pop the values. The one gotcha is that we do then have to push two values back on:
{
@n
1 1
{
@[a b n] !2 # take a, b and n (ignored), return 2
b # new a
a b + # new b
}
n 2 - loop
} @fib
40 fib writeln
Of course, we get the same answer:
$ cargo run --release -- --file examples/fibonacci-loop-keep2.stack --compile > output/fibonacci-loop-keep2.c
Finished release [optimized] target(s) in 0.11s
Running `target/release/stacklang --file examples/fibonacci-loop-keep2.stack --compile`
$ clang -Ofast output/fibonacci-loop-keep2.c -o output/fibonacci-loop-keep2
$ time output/fibonacci-loop-keep2
102334155
real 0m0.088s
user 0m0.000s
sys 0m0.001s
And in debug mode, we can confirm that we’re not blowing up the stack this time:
$ cargo run -- --debug --file examples/fibonacci-loop-keep2.stack --compile > output/fibonacci-loop-keep2.c
Finished dev [unoptimized + debuginfo] target(s) in 0.08s
Running `target/debug/stacklang --debug --file examples/fibonacci-loop-keep2.stack --compile`
$ clang output/fibonacci-loop-keep2.c -o output/fibonacci-loop-keep2
$ output/fibonacci-loop-keep2
[DEBUG] block_0 called -- STACK: <empty>
[DEBUG] block_1 called -- STACK: 40 {block} NAMES: fib={block}
[DEBUG] block_2 called -- STACK: 0 1 1 40 {block} NAMES: n=40 | fib={block}
[DEBUG] block_2 return -- STACK: 2 1 40 {block} NAMES: n=0 b=2 a=1 n=40 | fib={block}
[DEBUG] block_2 called -- STACK: 1 2 1 40 {block} NAMES: n=40 | fib={block}
[DEBUG] block_2 return -- STACK: 3 2 40 {block} NAMES: n=1 b=3 a=2 n=40 | fib={block}
[DEBUG] block_2 called -- STACK: 2 3 2 40 {block} NAMES: n=40 | fib={block}
[DEBUG] block_2 return -- STACK: 5 3 40 {block} NAMES: n=2 b=5 a=3 n=40 | fib={block}
[DEBUG] block_2 called -- STACK: 3 5 3 40 {block} NAMES: n=40 | fib={block}
[DEBUG] block_2 return -- STACK: 8 5 40 {block} NAMES: n=3 b=8 a=5 n=40 | fib={block}
[DEBUG] block_2 called -- STACK: 4 8 5 40 {block} NAMES: n=40 | fib={block}
[DEBUG] block_2 return -- STACK: 13 8 40 {block} NAMES: n=4 b=13 a=8 n=40 | fib={block}
...
Pretty cool.
With a recursive helper
And finally, just to show that we can, we can also write the function without using loop at all, instead rewriting the above ’loop-keep2’ in a recursive style:
{
@n
{
@[n a b]
b
{
@0 !1
(n 1 -) (a b +) a fibacc
}
n 1 <= if
} @fibacc
n 1 1 fibacc
} @fib
40 fib writeln
In this case, we define a hidden/helper function: fibacc, only visible when inside of the fib block. In this case, fibacc explicitly takes three variables: n (to control recursion) and a/b. If n is small enough, base case. Otherwise, update a and b and recur.
And of course, it works the same (and just about as fast):
$ cargo run --release -- --file examples/fibonacci-acc.stack --compile > output/fibonacci-acc.c
Finished release [optimized] target(s) in 0.08s
Running `target/release/stacklang --file examples/fibonacci-acc.stack --compile`
$ clang -Ofast output/fibonacci-acc.c -o output/fibonacci-acc
$ time output/fibonacci-acc
102334155
real 0m0.083s
user 0m0.000s
sys 0m0.001s
Unfortunately, we don’t (yet) have any sort of {{wikipedia “tail call optimization”}}, so each of those values (as we’re recursively calling) is kept on the stack:
$ cargo run -- --debug --file examples/fibonacci-acc.stack --compile > output/fibonacci-acc.c
Finished dev [unoptimized + debuginfo] target(s) in 0.08s
Running `target/debug/stacklang --debug --file examples/fibonacci-acc.stack --compile`
$ clang output/fibonacci-acc.c -o output/fibonacci-acc
$ output/fibonacci-acc
[DEBUG] block_0 called -- STACK: <empty>
[DEBUG] block_1 called -- STACK: 40 {block} NAMES: fib={block}
[DEBUG] block_2 called -- STACK: 1 1 40 {block} 40 {block} NAMES: fibacc={block} | n=40 fib={block}
[DEBUG] block_3 called -- STACK: 1 1 40 {block} 40 {block} NAMES: b=1 | a=1 n=40 fibacc={block} | n=40 fib={block}
[DEBUG] block_2 called -- STACK: 1 2 39 1 1 40 {block} 40 {block} NAMES: b=1 | a=1 n=40 fibacc={block} | n=40 fib={block}
[DEBUG] block_3 called -- STACK: 1 2 39 1 1 40 {block} 40 {block} NAMES: b=1 | a=2 n=39 b=1 | a=1 n=40 fibacc={block} | n=40 fib={block}
[DEBUG] block_2 called -- STACK: 2 3 38 1 2 39 1 1 40 {block} 40 {block} NAMES: b=1 | a=2 n=39 b=1 | a=1 n=40 fibacc={block} | n=40 fib={block}
[DEBUG] block_3 called -- STACK: 2 3 38 1 2 39 1 1 40 {block} 40 {block} NAMES: b=2 | a=3 n=38 b=1 | a=2 n=39 b=1 | a=1 n=40 fibacc={block} | n=40 fib={block}
[DEBUG] block_2 called -- STACK: 3 5 37 2 3 38 1 2 39 1 1 40 {block} 40 {block} NAMES: b=2 | a=3 n=38 b=1 | a=2 n=39 b=1 | a=1 n=40 fibacc={block} | n=40 fib={block}
[DEBUG] block_3 called -- STACK: 3 5 37 2 3 38 1 2 39 1 1 40 {block} 40 {block} NAMES: b=3 | a=5 n=37 b=2 | a=3 n=38 b=1 | a=2 n=39 b=1 | a=1 n=40 fibacc={block} | n=40 fib={block}
[DEBUG] block_2 called -- STACK: 5 8 36 3 5 37 2 3 38 1 2 39 1 1 40 {block} 40 {block} NAMES: b=3 | a=5 n=37 b=2 | a=3 n=38 b=1 | a=2 n=39 b=1 | a=1 n=40 fibacc={block} | n=40 fib={block}
[DEBUG] block_3 called -- STACK: 5 8 36 3 5 37 2 3 38 1 2 39 1 1 40 {block} 40 {block} NAMES: b=5 | a=8 n=36 b=3 | a=5 n=37 b=2 | a=3 n=38 b=1 | a=2 n=39 b=1 | a=1 n=40 fibacc={block} | n=40 fib={block}
[DEBUG] block_2 called -- STACK: 8 13 35 5 8 36 3 5 37 2 3 38 1 2 39 1 1 40 {block} 40 {block} NAMES: b=5 | a=8 n=36 b=3 | a=5 n=37 b=2 | a=3 n=38 b=1 | a=2 n=39 b=1 | a=1 n=40 fibacc={block} | n=40 fib={block}
...
Oy. Back to exploding the stack!
Something to work on in the future though!
Complex numbers
Okay, we’ve done a lot of math. Let’s move on … to more math!
At this time, I don’t yet have complex numbers implemented as a native datatype as I’d like. But that doesn’t matter, since with arbitrarily many parameters and return values, we can just directly implement them!
{
@[ar ai br bi] !2
ar br * ai bi * -
ar bi * ai br * +
} @cmul
{
@[ar ai br bi] !2
ar br +
ai bi +
} @cadd
{
@[r i] !0
r write
"+" write
i write
"i" write
} @cwrite
"multiply:" writeln
3 -2 4 5 cmul cwrite newline
22 7 cwrite newline
newline
"add:" writeln
3 -2 4 5 cadd cwrite newline
7 3 cwrite newline
So each of the functions takes 2 parameters: the real and imaginary part of a complex number. Then in the case of cmul and cadd, we return 2 as well: the new real and imaginary parts.
The naming really helps here.
Mandelbrot
And then finally, the piece de resistance, using those complex numbers to calculate the Mandelbrot set!
I’m not going to talk through the code this time, since it’s pretty much a direct translation of the algorithm (see the link above). But I do think it’s a good example of how you can start to write ‘real code’ in StackLang:
# Set image dimensions and maximum number of iterations
1920 @width
1080 @height
16 @max_iterations
# Set the range of complex numbers to visualize
-2.0 @min_real
1.0 @max_real
-1.0 @min_imag
1.0 @max_imag
# Calculate the step sizes for the real and imaginary parts
max_real min_real - width / @real_step
max_imag min_imag - height / @imag_step
{
@[ar ai br bi] !2
ar br * ai bi * -
ar bi * ai br * +
} @cmul
{
@[ar ai br bi] !2
ar br +
ai bi +
} @cadd
{
@[r i]
r i * r i * +
} @cmag2
{
@[px py max_iter]
{
@[zx zy i iter]
0
{
@0 !1
i
{
@0 !1
zx zy zx zy cmul px py cadd
i 1 +
$iter iter
}
zx zy cmag2 4.0 > if
}
i max_iter = if
} @iter
px py 1 $iter iter
} @mandelbrot
# Write the PPM header
"P3" writeln
width writeln
height writeln
"255" writeln
# Loop through image rows (y) and columns (x)
{
@y
{
@x
# Calculate the current complex number (real + imag * i)
x real_step * min_real + @real
y imag_step * min_imag + @imag
# Calculate the number of iterations for the current complex number
real imag max_iterations mandelbrot @iterations
# Scale the number of iterations to a color value (assuming grayscale)
1.0 iterations * max_iterations / 255 * to_int @color
# Write the color value to the PPM file (red, green, blue)
color write " " write
color write " " write
color write " " write
} width loop
newline
} height loop
And with the compiler, it’s relatively quick:
$ cargo run --release -- --file examples/mandelbrot.stack --compile > output/mandelbrot.c
Finished release [optimized] target(s) in 0.07s
Running `target/release/stacklang --file examples/mandelbrot.stack --compile`
$ clang -Ofast output/mandelbrot.c -o output/mandelbrot
$ time output/mandelbrot | convert - output/mandelbrot-compile.png
real 0m10.250s
user 0m9.599s
sys 0m0.101s

Taking user input; now with more colors!
As one last aside though, we have implemented read into the language. This reads a single line from stdin and stores it as a string. We can then use to_int to convert it and thus parameterize our mandelbrot function!
# Set image dimensions and maximum number of iterations
read to_int @width
read to_int @height
read to_int @max_iterations
...
Likewise, we can tweak the color algorithm to use the value not as grayscale but rather in the red and green channels:
# Write the color value to the PPM file (red, green, blue)
color write " " write
255 color - write " " write
0 write " " write
Now we run it again, this time providing the size at runtime:
$ cargo run --release -- --file examples/mandelbrot-read.stack --compile > output/mandelbrot-read.c
Finished release [optimized] target(s) in 0.10s
Running `target/release/stacklang --file examples/mandelbrot-read.stack --compile`
$ clang -Ofast output/mandelbrot-read.c -o output/mandelbrot-read
$ output/mandelbrot-read
# Note: These three lines are user input
# I can't write a prompt (yet) because I'm redirecting stdout to a PPM file
# Normally (and in the future) this would be done by using stderr for the prompt
1920
1080
16
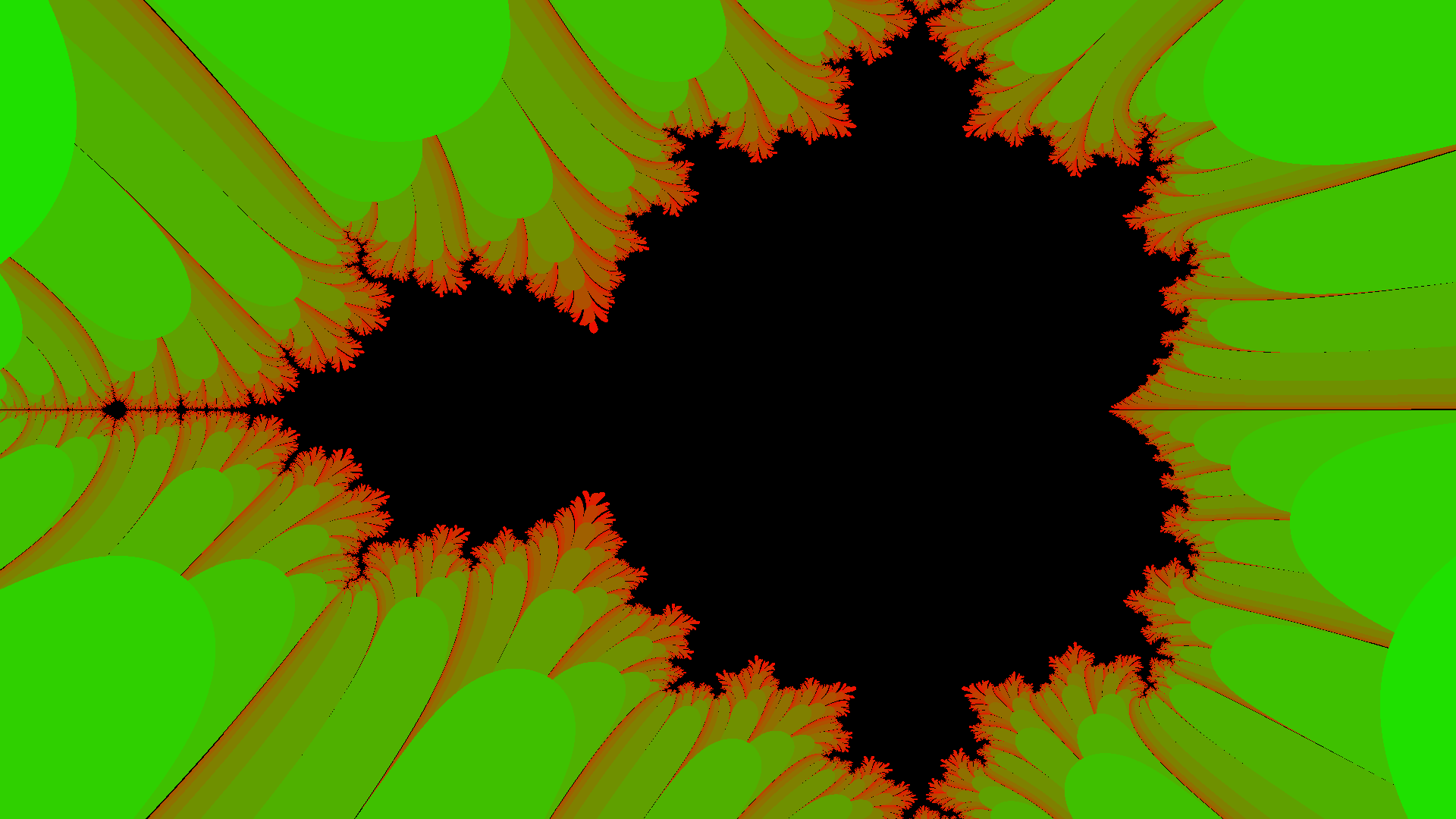
Whee!
Well, that’s all for today. I’ve certainly got a few things to work on. So let’s see where we can go from here!