Source: Monkey Math
Part 1
Given a series of equations of either the form
dbpl: 5orcczh: sllz + lgvd, determine what the value of the node labeledrootis.
Originally, I set this up with a proper graph/tree structure:
#[derive(Debug)]
enum Monkey {
Constant { value: INumber },
Math {
op: Op,
parents: Weak<RefCell<Monkey>>,
left: Rc<RefCell<Monkey>>,
right: Rc<RefCell<Monkey>>,
},
}
Where Weak is an Rc that doesn’t count towards the current reference count and will become None if the value goes out of scope (if all related Rc go out of scope) first. But I had one heck of a time actually getting the thing to go together. I really need to work through one of the various [other posts](about it). But for the moment, I just went for a much easier approach:
#[derive(Debug)]
enum Monkey {
Human,
Constant { value: INumber },
Math { op: Op, left: String, right: String },
}
#[derive(Debug)]
struct Troop {
monkeys: HashMap<String, Rc<Monkey>>,
}
impl Troop {
fn new() -> Self {
Troop {
monkeys: HashMap::new(),
}
}
}
The Troop will handle most of the work, the Monkey only needs to get the references. At least, as an enum, I can have a difference between Constant monkeys and Math monkeys. The latter also have Ops:
#[derive(Debug)]
struct Op {
f: fn(INumber, INumber) -> INumber,
name: String,
}
impl From<&str> for Op {
fn from(text: &str) -> Self {
Op {
name: String::from(text),
f: match text {
"+" => |a, b| a + b,
"-" => |a, b| a - b,
"*" => |a, b| a * b,
"/" => |a, b| a / b,
_ => panic!("unknown op: {text}"),
},
}
}
}
What we really need though is the ability to parse a Troop as a Vec<Monkey>:
impl Troop {
fn add(&mut self, line: &String) {
// Simple/constant value monkey
if line.chars().filter(|c| c.is_whitespace()).count() == 1 {
let (name, value) = line
.split_ascii_whitespace()
.collect_tuple()
.expect("Constant monkey must be '{name}: {value}'");
let name = String::from(
name.strip_suffix(":")
.expect("Constant monkey name must have :"),
);
let value = value
.parse::<INumber>()
.expect("Constant monkey value must be numeric");
self.monkeys
.insert(name, Rc::new(Monkey::Constant { value: value }));
}
// Mathematical monkey
else {
let (name, left, op_name, right) = line
.split_ascii_whitespace()
.collect_tuple()
.expect("Math monkey must be '{name}: {name} {op} {name}'");
let name = String::from(
name.strip_suffix(":")
.expect("Constant monkey name must have :"),
);
let op = Op::from(op_name);
let left = String::from(left);
let right = String::from(right);
self.monkeys.insert(
String::from(name),
Rc::new(Monkey::Math { op, left, right }),
);
}
}
}
With that in place, we can try the relatively brute force method of asking the Troop to calculate the value of the root monkey. It will handle the recursion, it just needs to get the Op and the names of the left and right Monkeys (Constants are much easier).
impl Troop {
fn value(&self, name: &String) -> INumber {
match &self.monkeys[name].as_ref() {
Monkey::Constant { value } => *value,
Monkey::Math {
op: Op { f, .. },
left,
right,
..
} => f(self.value(left), self.value(right)),
_ => panic!("humans have no value"),
}
}
}
And wrap it up:
fn part1(filename: &Path) -> String {
let mut troop = Troop::new();
for line in iter_lines(filename) {
troop.add(&line);
}
troop.value(&String::from("root")).to_string()
}
I was worried that the timing specified in the original problem would come into play somehow (like there would be cycles in there). But… it seems not.
Actually, I did something similar to what I did in AoC 2022 Day 16: Pressurinator and decided to make a method that would render the entire Troop out as a graph (using graphviz). It’s… a lot:
If you’d like to see the whole thing, you can try opening it in a new tab.
For a more manageable example though, here’s the test data instead:
Nothing interesting about that. 😄
Part 2
Replace the
rootnode with the=operator. Find the value for the constanthumnnode that makes therootequality true.
Oh, that’s fun.
So of course, my first idea was just to brute force it. Find the humn node and keep trying different values until root was equal. In the test case, the answer is only 301 and there were only a dozen or so nodes, so this was pretty quick.
In the full data…
Somewhat less so.
So the next thing that I wanted to do was to simplify that tree dramatically.
Constant folding
The first optimization I thought of was constant folding / simplify_constants. Essentially, for any branch of the tree that doesn’t include the humn node, we should be able to reduce the whole thing to a single value. Rather than doing it all at once though, all we have to do is fine a node such that:
- the parent node is a
Mathnode - both children are
Constantnodes
If that’s the case, replace the parent with a new Constant node that applies the operation ‘ahead of time’. Something like this:
impl Troop {
// Simplify all non-human and non-human-dependant lifeforms
// If both children of a node are constant, apply the expression
// Do not simplify the 'humn' node
fn simplify_constants(&mut self) {
loop {
let mut target = None;
'found_one: for (name, monkey) in self.monkeys.iter() {
match monkey.as_ref() {
Monkey::Math {
op: Op { f, .. },
left,
right,
..
} => {
if left.as_str() == "humn" || right.as_str() == "humn" {
continue;
}
if let Some(response) = self
.monkeys
.get(left)
.and_then(|m| m.try_constant_value())
.and_then(|left_value| {
self.monkeys
.get(right)
.and_then(|m| m.try_constant_value())
.and_then(|right_value| {
Some((name.clone(), f(left_value, right_value)))
})
})
{
target = Some(response);
break 'found_one;
}
}
_ => continue,
}
}
if let Some((name, value)) = target {
self.monkeys
.insert(name, Rc::new(Monkey::Constant { value }));
continue;
}
break;
}
self.remove_dead_nodes();
}
}
I did hardcode humn here as the node we’re ignoring and the nested let Some + and_then etc is pretty crazy looking, but it ends up working out pretty well. I did end up writing a later function that simplifies a whole bunch of this on Monkey:
impl Monkey {
fn is_human(&self) -> bool {
match self {
Monkey::Human => true,
_ => false,
}
}
fn try_constant_value(&self) -> Option<INumber> {
match self {
Monkey::Constant { value } => Some(*value),
_ => None,
}
}
}
But I haven’t gone back to clean it up, since it just worked so well. At the end, I did do one more pass (remove_dead_nodes) that cleans the data structure up. Any nodes that are no longer connected to anything get removed. This isn’t at all necessary, since they’re not attached so don’t impact runtime, but it was nice for generating the graphs:
impl Troop {
// Remove all monkeys that aren't root and aren't referenced by any others
fn remove_dead_nodes(&mut self) {
let to_remove = self
.monkeys
.iter()
.filter(|(potential, _)| {
!self.monkeys.iter().any(|(_, monkey)| {
potential.as_str() == "root"
|| match monkey.as_ref() {
Monkey::Math { left, right, .. } => {
left == *potential || right == *potential
}
_ => false,
}
})
})
.map(|(name, _)| name.clone())
.collect::<Vec<_>>();
for name in to_remove.iter() {
self.monkeys.remove(&name.clone());
}
}
}
And with that, we have our first pass:
That looks like it should be much easier… but what about the full case?
Yeah… okay, that’s still quite a lot.
Simplify equality
Next up, let’s use the fact that there’s a big-ol equal sign on the top and do some rewriting. Something like this:
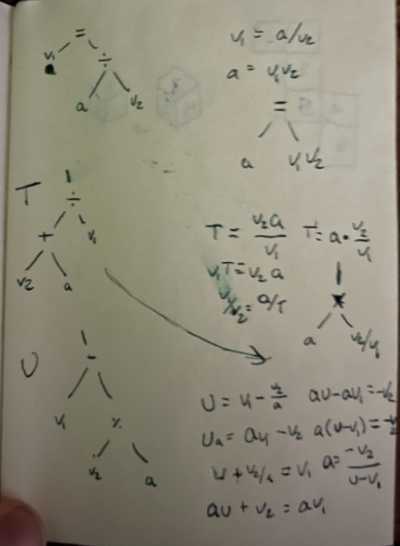
It’s always handy to have a notebook around. :D
Essentially, if you have a structure like this:
Such that there’s a constant on one side and a constant + a subtree on the other, you can simplify it like this:
Since there are only constants on the new left side, you can evaluate that and then that will give you a new node with the same style.
There are just two (bigger) complications:
- There are four possible cases depending on if the first constant is on the left or right and if the second constant is on the left or right within it’s subtree
- The inverses are not all obvious (it’s not as simple as
+<=>-, since the minus might have the constant on either side)
I’m not sure how to describe this other than to show you the (rather long) code that I eventually got working:
impl Troop {
// Simplify cases where one first level and one second level child are constant
fn simplify_equality(&mut self) {
let rc_self = Rc::new(RefCell::new(self));
let mut name_count = 0;
'found_human: for _i in 1.. {
let root = rc_self.clone().borrow().monkeys[&String::from("root")].clone();
if root.try_op_name().is_none() || root.try_op_name().unwrap() != "=" {
panic!("root must be = to use this method");
}
let left_name = root.try_math_left().unwrap().clone();
let left = rc_self.clone().borrow().monkeys[&left_name].clone();
let right_name = root.try_math_right().unwrap().clone();
let right = rc_self.clone().borrow().monkeys[&right_name].clone();
let mut v_level_1 = None; // First level value
let mut v_level_1_is_left = false;
let mut v_level_2 = None; // Second level value
let mut v_level_2_is_left = false;
let mut op_name = None;
let mut t_level_2 = None;
let mut to_remove = vec![left_name.clone(), right_name.clone()];
if left.is_human() || right.is_human() {
break 'found_human;
}
// Left is the constant side
if let Some(lv) = left.try_constant_value() {
v_level_1 = Some(lv);
v_level_1_is_left = true;
op_name = Some(right.try_op_name().unwrap().clone());
// Right left is the other constant
if let Some(rlv) = rc_self.clone().borrow().monkeys[&right.try_math_left().unwrap()]
.try_constant_value()
{
v_level_2 = Some(rlv);
v_level_2_is_left = true;
t_level_2 = Some(right.try_math_right().unwrap());
to_remove.push(right.try_math_left().unwrap().clone());
}
// Right right is the other constant
else if let Some(rrv) = rc_self.clone().borrow().monkeys
[&right.try_math_right().unwrap()]
.try_constant_value()
{
v_level_2 = Some(rrv);
v_level_2_is_left = false;
t_level_2 = Some(right.try_math_left().unwrap());
to_remove.push(right.try_math_right().unwrap().clone());
}
// Something went wrong
else {
panic!("neither child of right ({right:?}) is constant");
}
}
// Right is the constant side
else if let Some(rv) = right.try_constant_value() {
v_level_1 = Some(rv);
v_level_1_is_left = false;
op_name = Some(left.try_op_name().unwrap().clone());
// Left left is the other constant
if let Some(llv) = rc_self.clone().borrow().monkeys[&left.try_math_left().unwrap()]
.try_constant_value()
{
v_level_2 = Some(llv);
v_level_2_is_left = true;
t_level_2 = Some(left.try_math_right().unwrap());
to_remove.push(left.try_math_left().unwrap().clone());
}
// Left right is the other constant
else if let Some(lrv) = rc_self.clone().borrow().monkeys
[&left.try_math_right().unwrap()]
.try_constant_value()
{
v_level_2 = Some(lrv);
v_level_2_is_left = false;
t_level_2 = Some(left.try_math_left().unwrap());
to_remove.push(left.try_math_right().unwrap().clone());
}
// Something went wrong
else {
panic!("neither child of left ({left:?}) is constant");
}
}
// Something went wrong
else {
panic!(
"neither left nor root of root is constant, left: {left:?}, right: {right:?}"
);
}
// Build and attach the new root and frankenmonkey
// Calculate the various possible inverse functions
// The annoying one was [[v2 - SUB] = v1] since you need to subtract v2 and then negate
// I haven't handled all of the cases, just the ones that actually show up in the problem
let op_name = op_name.unwrap();
let f_inverse = match (op_name.as_str(), v_level_2_is_left) {
("+", _) => |v1, v2| v1 - v2,
("-", true) => |v1, v2| -1 * (v1 - v2),
("-", false) => |v1, v2| v1 + v2,
("*", _) => |v1, v2| v1 / v2,
("/", false) => |v1, v2| v1 * v2,
_ => panic!("unknown pattern ({op_name}, {v_level_2_is_left})"),
};
// Generate new, unique names for each monkey
let new_monkey_name = format!("C_{name_count}");
name_count += 1;
// Build and insert the new monkey with a constant value based on f_inverse above
let new_monkey = Monkey::Constant {
value: f_inverse(v_level_1.unwrap(), v_level_2.unwrap()),
};
rc_self
.clone()
.borrow_mut()
.monkeys
.insert(new_monkey_name.clone(), Rc::new(new_monkey));
// Figure out which side we should re-insert the new and old SUB monkes
let t_level_2_name = t_level_2.unwrap();
let left_name = if v_level_1_is_left {
new_monkey_name.clone()
} else {
t_level_2_name.clone()
};
let right_name = if v_level_1_is_left {
t_level_2_name.clone()
} else {
new_monkey_name.clone()
};
// Replace the new root node with one a single level down
rc_self.clone().borrow_mut().monkeys.insert(
String::from("root"),
Rc::new(Monkey::Math {
op: Op::from("="),
left: left_name,
right: right_name,
}),
);
// Remove the nodes that we no longer have in our tree (the constant values + what became the root)
for name in to_remove.into_iter() {
rc_self.borrow_mut().monkeys.remove(&name);
}
}
}
}
Originally, I had the rebuilding in each of the 4 branches, but that ran afoul of Rust’s borrow checker (specifically the runtime one in RefCell), since I was borrowing the data immutably once to find the nodes and then trying to mutably borrow again to change them. Rightfully so, this isn’t safe, since I’m potentially blowing up the tree while the nodes I’m working on are still (immutably) in scope.
So instead, this structure, where I first find the nodes, then after those borrows go out of scope, I can create and modify the new nodes.
As I mentioned, the inverse ops were a bit interesting:
// Calculate the various possible inverse functions
// The annoying one was [[v2 - SUB] = v1] since you need to subtract v2 and then negate
// I haven't handled all of the cases, just the ones that actually show up in the problem
let op_name = op_name.unwrap();
let f_inverse = match (op_name.as_str(), v_level_2_is_left) {
("+", _) => |v1, v2| v1 - v2,
("-", true) => |v1, v2| -1 * (v1 - v2),
("-", false) => |v1, v2| v1 + v2,
("*", _) => |v1, v2| v1 / v2,
("/", false) => |v1, v2| v1 * v2,
_ => panic!("unknown pattern ({op_name}, {v_level_2_is_left})"),
};
Specifically subtraction. Addition and multiplication are easy, since those have the commutative property, but subtraction is trickier (since you need to subtract than negate in one case but just add in the other). I never did the second case for division, it just didn’t come up in the puzzle.
Other than that, it was just a matter of iterating on the code until everything made sense. I made rather a few more graphs of this all working:
And in the end, we have our answer:
fn part2(filename: &Path) -> String {
let mut troop = Troop::new();
for mut line in iter_lines(filename) {
// Hacky, :shrug:
if line.starts_with("root:") {
line = line
.replace("+", "=")
.replace("-", "=")
.replace("*", "=")
.replace("/", "=");
}
troop.add(&line);
}
troop
.monkeys
.insert(String::from("humn"), Rc::new(Monkey::Human));
troop.simplify_constants();
troop.simplify_equality();
let root = &troop.monkeys[&String::from("root")];
let left = &troop.monkeys[&root.try_math_left().unwrap()];
let right = &troop.monkeys[&root.try_math_right().unwrap()];
if left.is_human() {
right.try_constant_value().unwrap().to_string()
} else if right.is_human() {
left.try_constant_value().unwrap().to_string()
} else {
panic!("absolutely murdered the human")
}
}
I did add a new Human variant to the Monkey enum just so it wouldn’t be automatically simplified, but other than that, it’s just a matter of figuring out which is the remaining humn node and returning the other.
I … may have had a little too much fun with some of the comments and messages in this one.
Rendering dot files
As a quick aside, here’s the code that I used to render a Troop as a Graphviz .dot file:
impl Troop {
fn dot(&self, graph_name: &str) -> String {
let mut result = format!("graph {graph_name} {{\n");
for (name, monkey) in self.monkeys.iter() {
match monkey.as_ref() {
Monkey::Constant { value } => {
result.push_str(
format!("\t\"{graph_name}.{name}\" [label=\"{name}\\n{value}\"];\n")
.as_str(),
);
}
Monkey::Math {
op: Op { name: op_name, .. },
left,
right,
..
} => {
result.push_str(format!("\t\"{graph_name}.{name}\" [label=\"{name}\\n{op_name}\", ordering=\"out\"];\n").as_str());
result.push_str(
format!(
"\t\t\"{graph_name}.{name}\" -- \"{graph_name}.{left}\" [label=L];\n"
)
.as_str(),
);
result.push_str(
format!(
"\t\t\"{graph_name}.{name}\" -- \"{graph_name}.{right}\" [label=R];\n"
)
.as_str(),
);
}
Monkey::Human => {
result.push_str(
format!("\t\"{graph_name}.humn\" [label=\"HELPME!\"];\n").as_str(),
);
}
}
}
result.push('}');
result
}
}
I named the graphs and prefix all of the node names so that I can actually display more than one of them in a subgraph. Helpful when I was looking at a whole pile of them. My graphviz installation didn’t much like doing the entire full test case like this though. 😄
Performance
$ ./target/release/21-yellinator 1 data/21.txt
31017034894002
took 4.292541ms
$ ./target/release/21-yellinator 2 data/21.txt
3555057453229
took 27.803ms
That took much longer to think about and work out the second optimization than it would have had I just done the problem by hand, but so it goes.