Source: Proboscidea Volcanium
Part 1
Given a graph of nodes, some of which have a
pressure(per tick output value) and an agent that can move through the graph and activate specific nodes (so that they output their per tick value every future tick), what is the maximum total output possible in 30 steps?
Oooh, that’s fun. I took a long time optimizing this one over and over again to get it to actually solve even part 1. I have to admit… I don’t actually have a part 2 solution yet that will run in a reasonable amount of time (and more importantly with a reasonable amount of RAM). I’ll update this post when I do…
But in any case, on to the solution.
As always, the first goal is to store the cave:
// Store the description of the cave as a directed graph with flow rates at the nodes
#[derive(Debug)]
struct Cave {
size: usize,
names: Vec<String>,
indexes: HashMap<String, usize>,
flow_rates: Vec<usize>,
distances: Matrix<usize>,
}
We’re using the Matrix class we defined earlier, otherwise nothing out of the ordinary. Parsing uses the regex tricks from yesterday:
// Parse a graph from a string iterator
impl<I> From<&mut I> for Cave
where
I: Iterator<Item = String>,
{
fn from(iter: &mut I) -> Self {
let mut names = Vec::new();
let mut indexes = HashMap::new();
let mut flow_rates = Vec::new();
let mut neighbors = HashMap::new();
let re = Regex::new(
r"Valve (\w+) has flow rate=(\d+); tunnels? leads? to valves? ((?:\w+)(?:, \w+)*)",
)
.expect("regex creation failed");
for (index, line) in iter.enumerate() {
let caps = re.captures(&line).expect("regex doesn't match line");
let name = String::from(&caps[1]);
neighbors.insert(
name.clone(),
caps[3]
.split(", ")
.map(|s| (1, String::from(s)))
.collect::<Vec<_>>(),
);
indexes.insert(name.clone(), index);
names.push(name);
flow_rates.push(caps[2].parse::<usize>().unwrap());
}
let size = names.len();
// Write distances as a matrix
let mut distances = Matrix::<usize>::new(size, size);
for i in 0..size {
for j in 0..size {
distances[[i, j]] = usize::MAX;
}
}
for (src, neighbors) in neighbors.iter() {
for (distance, dst) in neighbors.iter() {
distances[[indexes[src], indexes[dst]]] = *distance;
}
}
Cave {
size: names.len(),
names,
indexes,
flow_rates,
distances,
}
}
}
So originally, I define a single step as:
- moving between any two connected nodes
- enabling the current node
There’s a much better way to do this, but we’ll come back to that.
The basic idea of the original solution was:
- Define a function
recurthat takes in the current location, remaining fuel, and which locations are enabled - Calculate a base case result of doing nothing for the rest of the simulation (
result) - If the current location isn’t enabled, fire off a
recursive solution that does anEnablestep now and then finds the best recursive solution; if this is better thanresult, it becomesresult - For each neighboring node, do the same, calculate
recurforMove(node)and if the recursive solution there is better, then take that result
Technically correct… but very slow. I don’t actually even have runtimes for this one.
I did have one way that I could at least make it bearable though: memoization. Essentially, cache the result of each recursive call, that way if I end up in the same state through another branch (such as if A -> B -> C, A -> D -> C, then moving down either path results in the same recur calls.)
To implement that, I added this to my max_flow function:
// Flow algorithms for a cave
impl Cave {
// Find the steps for maximizing flow from a single location with a single agent
fn max_flow(self, location: String, fuel: usize) -> (usize, Vector<Step>) {
type CacheKey = (usize, usize, Vector<bool>);
type CacheValue = (usize, Vector<Step>);
// The memoized recursive function that actually does the work
// cave and cache don't change
// index is where the agent currently is
// fuel is how much fuel is left in the simulation (stop at 0)
// enabled is a list of which cave pumps are currently enabled
fn recur(
cave: Rc<Cave>,
cache: Rc<RefCell<HashMap<CacheKey, CacheValue>>>,
index: usize,
fuel: usize,
enabled: Vector<bool>,
) -> CacheValue {
// If we have already calculated a result at this index/fuel/enabled, return it
let cache_key = (index, fuel, enabled.clone());
if cache.borrow().contains_key(&cache_key) {
return cache.borrow_mut()[&cache_key].clone();
}
...
// Store the result in the cache and return it
cache.borrow_mut().insert(cache_key, result.clone());
result
}
// Fire off the recursive function
let cave = Rc::new(self);
recur(
cave.clone(),
Rc::new(RefCell::new(HashMap::new())),
cave.clone().indexes[&location],
fuel,
Vector::from(vec![false; cave.clone().size]),
)
}
}
Don’t worry, we’ll get to the core of the algorithm. In a nutshell though, we pass around the cache (with Rc, so it’s cheap enough) and if we’ve already seen the same (index, fuel, enabled), we just return it.
Does this still work? Absolutely:
[ 1] Move("DD")
[ 2] Enable
[ 3] Move("CC")
[ 4] Move("BB")
[ 5] Enable
[ 6] Move("AA")
[ 7] Move("II")
[ 8] Move("JJ")
[ 9] Enable
[10] Move("II")
[11] Move("AA")
[12] Move("DD")
[13] Move("EE")
[14] Move("FF")
[15] Move("GG")
[16] Move("HH")
[17] Enable
[18] Move("GG")
[19] Move("FF")
[20] Move("EE")
[21] Enable
[22] Move("DD")
[23] Move("CC")
[24] Enable
[25] DoNothing
[26] DoNothing
[27] DoNothing
[28] DoNothing
[29] DoNothing
[30] DoNothing
1651
took 7.661355375s
This isn’t on my full data (with 59 nodes), this is just on the given test data (with only 10 nodes). And it already takes 7 seconds. With the full data, I think it took a few minutes to solve? Still perfectly reasonable, but… I knew I could do better.
Optimized version with multiple steps and no-repeats
Okay, the next way I attacked the problem was to optimize the number of choices we make at any given step to keep branching under control. To do that, I wanted to do a few things:
- Improve the
distancemap. If we can geta -> b -> c, then we can assume we can goa -> cusing 2 fuel. We can account for that. - Don’t go to nodes that are already enabled; anytime we go to a node, assume we’ll enable it, since the above accounts for moving through enabled nodes.
- Don’t go to nodes that have 0 flow; they’re functionally just connectors.
With all of this, there are only 7 branches at first, 6 after that, 5 after that and so on. A total of 7! = 5040 cases instead of 10 at every step.
Running on the test case:
./target/release/16-pressurinator 1 data/16-test.txt
Step(1, "DD")
Step(2, "BB")
Step(3, "JJ")
Step(7, "HH")
Step(3, "EE")
Step(2, "CC")
Step(4, "GG")
1651
took 40.906083ms
Ahyup, that’s much faster. Even on the full 59 nodes, there are only 23 that have a flow rate, so 23! = 2.58 * 10^22 . Yeah, okay that’s still a huge number. But remember the caching? Because of the relatively limited number of cases, it caches much better:
./target/release/16-pressurinator 1 data/16.txt
Step(2, "CA")
Step(2, "JF")
Step(3, "LE")
Step(3, "FP")
Step(2, "YH")
Step(2, "UX")
Step(2, "AR")
Step(4, "DM")
1720
took 175.448208ms
That… is acceptable.
The actual code
So… how does that work? First, expand the from function to calculate all distances:
// Parse a graph from a string iterator
impl<I> From<&mut I> for Cave
where
I: Iterator<Item = String>,
{
fn from(iter: &mut I) -> Self {
...
// Expand to calculate the minimum possible distance between nodes (of any number of steps)
// For any pair of nodes, if we don't have a distance:
// - Find a third node between them with a sum of of i->k->l == distance
// Because distance is increasing from 2 up, this will always fill in minimal values
loop {
let mut changed = false;
for i in 0..size {
for j in 0..size {
for k in 0..size {
if i == j || j == k || i == k {
continue;
}
if distances[[i, j]] == usize::MAX || distances[[j, k]] == usize::MAX {
continue;
}
let old_d = distances[[i, k]];
let new_d = distances[[i, j]] + distances[[j, k]];
if new_d < old_d {
changed = true;
distances[[i, k]] = new_d;
}
}
}
}
if !changed {
break;
}
}
Cave {
size: names.len(),
names,
indexes,
flow_rates,
distances,
}
}
}
For each possible triple of nodes (i, j, k), see if we can add a new node i, k distance via j / update the previous one with a better answer.
Now, we can use that do show the whole algorithm:
// A single step of the single agent simulation
#[derive(Clone, Debug, Hash, Eq, PartialEq, Ord, PartialOrd)]
struct Step(usize, String);
// Flow algorithms for a cave
impl Cave {
// Find the steps for maximizing flow from a single location with a single agent
fn max_flow(self, location: String, fuel: usize) -> (usize, Vector<Step>) {
type CacheKey = (usize, usize, Vector<bool>);
type CacheValue = (usize, Vector<Step>);
// The memoized recursive function that actually does the work
// cave and cache don't change
// index is where the agent currently is
// fuel is how much fuel is left in the simulation (stop at 0)
// enabled is a list of which cave pumps are currently enabled
fn recur(
cave: Rc<Cave>,
cache: Rc<RefCell<HashMap<CacheKey, CacheValue>>>,
index: usize,
fuel: usize,
enabled: Vector<bool>,
) -> CacheValue {
// If we have already calculated a result at this index/fuel/enabled, return it
let cache_key = (index, fuel, enabled.clone());
if cache.borrow().contains_key(&cache_key) {
return cache.borrow_mut()[&cache_key].clone();
}
// Calculate the current flow based on the enabled gates
let per_tick_flow = cave
.clone()
.flow_rates
.iter()
.zip(enabled.clone().iter())
.filter_map(|(f, c)| if *c { Some(*f) } else { None })
.sum::<usize>();
// Base case: try doing nothing for the rest of the simulation
let mut result = (fuel * per_tick_flow, Vector::new());
// Try each possible move
// A move is move to a node (inc multiple hops) + enable that node
for next_index in 0..cave.clone().size {
// Don't bother moving to something that's already on
// Don't bother moving to nodes with 0 flow
if index == next_index
|| enabled[next_index]
|| cave.clone().flow_rates[next_index] == 0
{
continue;
}
// Calculate the distance to this new node
// If we don't have enough fuel to make that trip, this isn't valid
let d = cave.clone().distances[[index, next_index]];
if d + 1 > fuel {
continue;
}
// Calculate which nodes will be enabled after this step
let mut next_enabled = enabled.clone();
next_enabled[next_index] = true;
// Recursively calculate the result from taking this step
let mut sub_result = recur(
cave.clone(),
cache.clone(),
next_index,
fuel - d - 1,
next_enabled,
);
// Update that result with the total flow from moving
// And the instruction for output
sub_result.0 += (d + 1) * per_tick_flow;
sub_result
.1
.push_front(Step(d, cave.clone().names[next_index].clone()));
// If that result is better than what we have so far, update our best result
result = result.max(sub_result);
}
// Store the result in the cache and return it
cache.borrow_mut().insert(cache_key, result.clone());
result
}
// Fire off the recursive function
let cave = Rc::new(self);
recur(
cave.clone(),
Rc::new(RefCell::new(HashMap::new())),
cave.clone().indexes[&location],
fuel,
Vector::from(vec![false; cave.clone().size]),
)
}
}
Everything is basically as I described above:
- Start with doing nothing
- For each remaining neighbor:
- If it’s not the current node
- AND if it’s not already enabled
- AND if it has a non-zero flow rate
- AND if we have enough fuel to get there
- Then we
recurdown that branch and use the best of these results
That’s really it.
One oddity is that there are a ton of clone() all over the place. This is actually perfectly fine, since I’m doing clone() on Rc. That basically means I’m making a new pointer to the same data structure and keeping track of all of them. There’s some small overhead, but it keeps Rust happy.
Optimally, I would have preferred to make this a closure with a single cave and cache captured from the environment instead, but this works well enough. I suppose making a new struct with cave and cache on the struct and recur as a method on it would have worked as well. C’est la vide.
Attempted to solve via 30 steps of all possibilities
As a quick aside, for a while, I tried a parallel approach where I would start in each state and then keep track of the ‘best’ way to get into each state for each step. The problem is, this doesn’t include the cases of both moving through a node and enabling it and not. So it’s not actually capable of optimizing this particular problem.
Tick 0
[state 0=AA] State(total: 0, current: 0, steps: [])
[state 1=BB] None
[state 2=CC] None
[state 3=DD] None
[state 4=EE] None
[state 5=FF] None
[state 6=GG] None
[state 7=HH] None
[state 8=II] None
[state 9=JJ] None
Tick 1
[state 0=AA] State(total: 0, current: 0, steps: [Enable])
[state 1=BB] State(total: 0, current: 0, steps: [Move(1, "BB")])
[state 2=CC] None
[state 3=DD] State(total: 0, current: 0, steps: [Move(1, "DD")])
[state 4=EE] None
[state 5=FF] None
[state 6=GG] None
[state 7=HH] None
[state 8=II] State(total: 0, current: 0, steps: [Move(1, "II")])
[state 9=JJ] None
Tick 2
[state 0=AA] State(total: 0, current: 0, steps: [Move(1, "II"), Move(1, "AA")])
[state 1=BB] State(total: 0, current: 13, steps: [Move(1, "BB"), Enable])
[state 2=CC] State(total: 0, current: 0, steps: [Move(1, "DD"), Move(1, "CC")])
[state 3=DD] State(total: 0, current: 20, steps: [Move(1, "DD"), Enable])
[state 4=EE] State(total: 0, current: 0, steps: [Move(1, "DD"), Move(1, "EE")])
[state 5=FF] None
[state 6=GG] None
[state 7=HH] None
[state 8=II] State(total: 0, current: 0, steps: [Enable, Move(1, "II")])
[state 9=JJ] State(total: 0, current: 0, steps: [Move(1, "II"), Move(1, "JJ")])
Tick 3
[state 0=AA] State(total: 20, current: 20, steps: [Move(1, "DD"), Enable, Move(1, "AA")])
[state 1=BB] State(total: 13, current: 13, steps: [Move(1, "BB"), Enable, DoNothing])
[state 2=CC] State(total: 20, current: 20, steps: [Move(1, "DD"), Enable, Move(1, "CC")])
[state 3=DD] State(total: 20, current: 20, steps: [Move(1, "DD"), Enable, DoNothing])
[state 4=EE] State(total: 20, current: 20, steps: [Move(1, "DD"), Enable, Move(1, "EE")])
[state 5=FF] State(total: 0, current: 0, steps: [Move(1, "DD"), Move(1, "EE"), Move(1, "FF")])
[state 6=GG] None
[state 7=HH] None
[state 8=II] State(total: 0, current: 0, steps: [Move(1, "II"), Move(1, "JJ"), Move(1, "II")])
[state 9=JJ] State(total: 0, current: 21, steps: [Move(1, "II"), Move(1, "JJ"), Enable])
Tick 4
[state 0=AA] State(total: 40, current: 20, steps: [Move(1, "DD"), Enable, DoNothing, Move(1, "AA")])
[state 1=BB] State(total: 40, current: 20, steps: [Move(1, "DD"), Enable, Move(1, "CC"), Move(1, "BB")])
[state 2=CC] State(total: 40, current: 22, steps: [Move(1, "DD"), Enable, Move(1, "CC"), Enable])
[state 3=DD] State(total: 40, current: 20, steps: [Move(1, "DD"), Enable, Move(1, "EE"), Move(1, "DD")])
[state 4=EE] State(total: 40, current: 23, steps: [Move(1, "DD"), Enable, Move(1, "EE"), Enable])
[state 5=FF] State(total: 40, current: 20, steps: [Move(1, "DD"), Enable, Move(1, "EE"), Move(1, "FF")])
[state 6=GG] State(total: 0, current: 0, steps: [Move(1, "DD"), Move(1, "EE"), Move(1, "FF"), Move(1, "GG")])
[state 7=HH] None
[state 8=II] State(total: 40, current: 20, steps: [Move(1, "DD"), Enable, Move(1, "AA"), Move(1, "II")])
[state 9=JJ] State(total: 21, current: 21, steps: [Move(1, "II"), Move(1, "JJ"), Enable, DoNothing])
Tick 5
[state 0=AA] State(total: 60, current: 20, steps: [Move(1, "DD"), Enable, Move(1, "AA"), Move(1, "II"), Move(1, "AA")])
[state 1=BB] State(total: 62, current: 22, steps: [Move(1, "DD"), Enable, Move(1, "CC"), Enable, Move(1, "BB")])
[state 2=CC] State(total: 62, current: 22, steps: [Move(1, "DD"), Enable, Move(1, "CC"), Enable, DoNothing])
[state 3=DD] State(total: 63, current: 23, steps: [Move(1, "DD"), Enable, Move(1, "EE"), Enable, Move(1, "DD")])
[state 4=EE] State(total: 63, current: 23, steps: [Move(1, "DD"), Enable, Move(1, "EE"), Enable, DoNothing])
[state 5=FF] State(total: 63, current: 23, steps: [Move(1, "DD"), Enable, Move(1, "EE"), Enable, Move(1, "FF")])
[state 6=GG] State(total: 60, current: 20, steps: [Move(1, "DD"), Enable, Move(1, "EE"), Move(1, "FF"), Move(1, "GG")])
[state 7=HH] State(total: 0, current: 0, steps: [Move(1, "DD"), Move(1, "EE"), Move(1, "FF"), Move(1, "GG"), Move(1, "HH")])
[state 8=II] State(total: 60, current: 20, steps: [Move(1, "DD"), Enable, DoNothing, Move(1, "AA"), Move(1, "II")])
[state 9=JJ] State(total: 60, current: 20, steps: [Move(1, "DD"), Enable, Move(1, "AA"), Move(1, "II"), Move(1, "JJ")])
A Priority Queue (Edit 2, Dec 20)
Continuing with the theme of making it faster, I decided to rewrite the max_flow function. Instead of being recursive, I’m going to keep the states to check in a priority queue, with the priority being the current flow.
The code isn’t that different:
// Flow algorithms for a cave
impl Cave {
// Find the steps for maximizing flow from a single location with a single agent
fn max_flow(self, start: String, fuel: usize) -> (usize, Vec<usize>) {
let mut queue = PriorityQueue::new();
queue.push((fuel, vec![self.indexes[start.as_str()]]), 0);
let mut best = (0, vec![0]);
while !queue.is_empty() {
let ((fuel, path), pressure) = queue.pop().unwrap();
if pressure > best.0 {
best = (pressure, path.clone());
}
for i in 0..self.size {
let d = self.distances[[*path.last().unwrap(), i]];
if path.contains(&i)
|| self.flow_rates[i] == 0
|| d + 1 > fuel {
continue;
}
let mut new_path = path.clone();
new_path.push(i);
queue.push(
(fuel - d - 1, new_path),
pressure + (fuel - d - 1) * self.flow_rates[i]
);
}
}
best
}
}
Makes for shorter, cleaner code too.
$ cargo run --release --bin 16-pressurinator 1 data/16.txt
Finished release [optimized] target(s) in 0.06s
Running `target/release/16-pressurinator 1 data/16.txt`
1720
took 100.268375ms
But… do I actually need a PriorityQueue? Since I’m actually going through all of the options anyways, and I don’t actually care about the order that much, can’t I just use a Vec as a stack?
// Flow algorithms for a cave
impl Cave {
// Find the steps for maximizing flow from a single location with a single agent
fn max_flow(self, start: String, fuel: usize) -> (usize, Vec<usize>) {
let mut queue = Vec::new();
queue.push((0, fuel, vec![self.indexes[start.as_str()]]));
let mut best = (0, vec![0]);
while !queue.is_empty() {
let (pressure, fuel, path) = queue.pop().unwrap();
if pressure > best.0 {
best = (pressure, path.clone());
}
for i in 0..self.size {
let d = self.distances[[*path.last().unwrap(), i]];
if path.contains(&i)
|| self.flow_rates[i] == 0
|| d + 1 > fuel {
continue;
}
let mut new_path = path.clone();
new_path.push(i);
queue.push((
pressure + (fuel - d - 1) * self.flow_rates[i],
fuel - d - 1,
new_path,
));
}
}
best
}
}
And it’s another step faster yet:
cargo run --release --bin 16-pressurinator 1 data/16.txt
Finished release [optimized] target(s) in 0.04s
Running `target/release/16-pressurinator 1 data/16.txt`
1720
took 72.882875ms
And that’s on my full test code which was previously running in about twice that time. Now… I just have to figure out how to apply that to part 2.
Part 2
Do the same only with two agents and 26 steps.
Now this is where things really got complicated. In a nutshell, I started out writing it with two index values plus adding a ttl value for each so that I knew how far along a given path we were. For that to work, I had essentially 4 blocks in my ‘choose which recur’ function:
If either agent had a
ttl = 0, they needed to choose where to go next.This was done the same way as above (try each node that isn’t
enabledand has aflow_rate > 0), I would set thettl = distance + 1, since it would takedistanceto get to the node and1more toenableit.The interesting bit of this one was that this branch didn’t actually use any fuel. It changed the agent, but because it didn’t use any fuel, I could do two of these (one for each agent) before moving on without breaking anything.
If either agent had a
ttl = 1, they were at a node and needed toenableit.This I did in a single case where I looped over all of the active agents and found all of them with
ttl = 1, settingenablefor all of them at once, then advancing 1 fuel for them and all the rest. This is also where I updated the flow (since flow doesn’t happen until the tick after anenablethis works). This would put any withttl = 1into thettl = 0case for the next tick.I did have to do this one all at once, because I can’t just tick some agents and not others, all agents had to tick at once.
One interesting thing is that this case only had one possible
recur(advance by 1 + set someenabledflags). We’ll come back to an implication of that in a bit.Finally, if all
ttl > 1, then we could advance time until we get to thettl = 1case. So find the minimum ttl and advance byminimum(ttl) - 1. This just adds the current flow to the total and otherwise doesn’t branch (like the above case).
Now this worked, but I was getting some odd bugs and the code was annoying to reason about. So what I really wanted was something a bit more elegant.
Simulating n agents
Enter the n-agent simulation. Instead of 2, we could have any number… even 1. For this, I made a State struct which contained the above index and ttl:
// The state of an agent in the multi agent simulation
#[derive(Copy, Clone, Debug, Hash, Eq, PartialEq)]
struct State {
index: usize,
ttl: usize,
}
impl State {
fn new(index: usize) -> State {
State { index, ttl: 0 }
}
fn tick(self, ticks: usize) -> State {
State {
index: self.index,
ttl: self.ttl - ticks,
}
}
}
Now the max_flow_multi function looks like this:
impl Cave {
// The same simulation but with multiple agents
fn max_flow_multi(
self,
location: String,
fuel: usize,
agents: usize,
) -> (usize, Vec<StepMulti>) {
type CacheKey = (Vec<State>, usize, BitVec);
type CacheValue = (usize, Vec<StepMulti>);
// Main recursive function with multiple agents
// cave and cache still don't change (other than to cache values)
// agents is an im::Vector of agent states, can be any number (even 1)
// - this contains the next index
// - plus a new value ttl which is how long it will take the agent to get to the index
// fuel is how long the simulation can still run
// enabled is the map of which flows are enabled
fn recur(
cave: Rc<Cave>,
cache: Rc<RefCell<HashMap<CacheKey, CacheValue>>>,
agents: Vector<State>,
fuel: usize,
enabled: Vector<Bool>,
) -> CacheValue {
// Cache based on the state of all agents/fuel/enabled
let cache_key = (agents.clone(), fuel, enabled.clone());
if cache.borrow().contains_key(&cache_key) {
return cache.borrow_mut()[&cache_key].clone();
}
...
}
// Init the agents and kick the recursive function off
let cave = Rc::new(self);
let (total_flow, steps) = recur(
cave.clone(),
Rc::new(RefCell::new(HashMap::new())),
Vector::from(vec![State::new(cave.clone().indexes[&location]); agents]),
fuel,
Vector::from(vec![0; cave.clone().size]),
);
// Because we're using Vec, the steps end up in reverse order
(total_flow, steps.into_iter().rev().collect::<Vec<_>>())
}
}
I’m still using Rc + RefCell for the cave and cache, but this time, I’m using im::Vector for the agents and the enabled field. In theory, these data structures are able to share a low of their structure between all of the different calls, only spending memory for the changes.
New multi-agent code with one agent
As a first case, I want to test if this actually works with a single agent. In theory, it should, because the scheduling will always be the same:
$ cargo run --release --bin 16-pressurinator 1 data/16-test.txt
Step(1, "DD")
Step(2, "BB")
Step(3, "JJ")
Step(7, "HH")
Step(3, "EE")
Step(2, "CC")
1651
took 5.135ms
$ cargo run --release --bin 16-pressurinator 2 data/16-test.txt
Schedule { fuel: 30, agent: 0, distance: 1, target: "DD" }
AdvanceTime { fuel: 30, ticks: 1 }
EnableTick { fuel: 29, activations: [(0, "DD")] }
Schedule { fuel: 28, agent: 0, distance: 2, target: "BB" }
AdvanceTime { fuel: 28, ticks: 2 }
EnableTick { fuel: 26, activations: [(0, "BB")] }
Schedule { fuel: 25, agent: 0, distance: 3, target: "JJ" }
AdvanceTime { fuel: 25, ticks: 3 }
EnableTick { fuel: 22, activations: [(0, "JJ")] }
Schedule { fuel: 21, agent: 0, distance: 7, target: "HH" }
AdvanceTime { fuel: 21, ticks: 7 }
EnableTick { fuel: 14, activations: [(0, "HH")] }
Schedule { fuel: 13, agent: 0, distance: 3, target: "EE" }
AdvanceTime { fuel: 13, ticks: 3 }
EnableTick { fuel: 10, activations: [(0, "EE")] }
Schedule { fuel: 9, agent: 0, distance: 2, target: "CC" }
AdvanceTime { fuel: 9, ticks: 2 }
EnableTick { fuel: 7, activations: [(0, "CC")] }
DoNothing { fuel: 6 }
1651
took 3.724916ms
That’s a good sign! And it’s actually faster somehow. It’s short enough that I’m not particularly worried about why for that now. So let’s try 2 agents.
Checking with multiple agents
$ cargo run --release --bin 16-pressurinator 2 data/16-test.txt
Step2 { fuel: 26, per_tick_flow: 0, data: Schedule { agent: 0, distance: 1, target: "DD" } }
Step2 { fuel: 26, per_tick_flow: 0, data: Schedule { agent: 1, distance: 1, target: "BB" } }
Step2 { fuel: 26, per_tick_flow: 0, data: AdvanceTime { ticks: 1 } }
Step2 { fuel: 25, per_tick_flow: 0, data: EnableTick { activations: [(0, "DD"), (1, "BB")] } }
Step2 { fuel: 24, per_tick_flow: 33, data: Schedule { agent: 0, distance: 4, target: "HH" } }
Step2 { fuel: 24, per_tick_flow: 33, data: Schedule { agent: 1, distance: 3, target: "JJ" } }
Step2 { fuel: 24, per_tick_flow: 33, data: AdvanceTime { ticks: 3 } }
Step2 { fuel: 21, per_tick_flow: 33, data: EnableTick { activations: [(1, "JJ")] } }
Step2 { fuel: 20, per_tick_flow: 54, data: Schedule { agent: 1, distance: 4, target: "CC" } }
Step2 { fuel: 20, per_tick_flow: 54, data: EnableTick { activations: [(0, "HH")] } }
Step2 { fuel: 19, per_tick_flow: 76, data: Schedule { agent: 0, distance: 3, target: "EE" } }
Step2 { fuel: 19, per_tick_flow: 76, data: AdvanceTime { ticks: 3 } }
Step2 { fuel: 16, per_tick_flow: 76, data: EnableTick { activations: [(0, "EE"), (1, "CC")] } }
Step2 { fuel: 15, per_tick_flow: 81, data: Schedule { agent: 0, distance: 4, target: "JJ" } }
Step2 { fuel: 15, per_tick_flow: 81, data: Schedule { agent: 1, distance: 5, target: "HH" } }
Step2 { fuel: 15, per_tick_flow: 81, data: AdvanceTime { ticks: 4 } }
Step2 { fuel: 11, per_tick_flow: 81, data: EnableTick { activations: [(0, "JJ")] } }
Step2 { fuel: 10, per_tick_flow: 81, data: Schedule { agent: 0, distance: 4, target: "EE" } }
Step2 { fuel: 10, per_tick_flow: 81, data: EnableTick { activations: [(1, "HH")] } }
Step2 { fuel: 9, per_tick_flow: 81, data: Schedule { agent: 1, distance: 7, target: "JJ" } }
Step2 { fuel: 9, per_tick_flow: 81, data: AdvanceTime { ticks: 3 } }
Step2 { fuel: 6, per_tick_flow: 81, data: EnableTick { activations: [(0, "EE")] } }
Step2 { fuel: 5, per_tick_flow: 81, data: Schedule { agent: 0, distance: 3, target: "HH" } }
Step2 { fuel: 5, per_tick_flow: 81, data: AdvanceTime { ticks: 3 } }
Step2 { fuel: 2, per_tick_flow: 81, data: EnableTick { activations: [(0, "HH"), (1, "JJ")] } }
Step2 { fuel: 1, per_tick_flow: 81, data: DoNothing }
1705
took 85.591208ms
It’s still pretty fast, even with the much larger search space! And it works! Almost.
But… that’s not actually the right answer. It’s really close, but I should be able to get a 1707 out of there instead of the 1705.
That… took some digging, but eventually, I figured it out. There’s an edge case (which this thankfully exposes) in the last non-enabled valve. If the two agents are not scheduling on the same tick (and they’re usually not), then whichever one finishes first will get scheduled to go to this node.
But what if that agent is on the completely other side of the simulation… The other agent (that finishes later) should be able to route to that index instead and leave the first one done to just do nothing instead.
In this case, I solved it by considering a special case once the number of nodes that have a non-zero flow that are not enabled is less than the number of agents, I relax the enabled[next_index] check, allowing them to go to an enabled node again. Like this (I’ll come back to the details for what else is going on here):
// Once all useful flows are active, allow moving to anywhere
let potential_enabled = cave
.clone()
.flow_rates
.iter()
.zip(enabled.clone())
.filter_map(|(f, e)| if *f > 0 && !e { Some(true) } else { None })
.count();
// If our TTL is 0, schedule our next move
// This doesn't advance time
if let Some((i, agent)) = agents.clone().iter().enumerate().find(|(_, a)| a.ttl == 0) {
for next_index in 0..cave.clone().size {
if agents.clone().iter().any(|a| next_inde
if agents.clone().iter().any(|a| next_index == a.index)
|| (potential_enabled >= agents.len() && enabled[next_index])
|| cave.clone().flow_rates[next_index] == 0
{
continue;
}
...
}
}
Because it’s late in the process, the performance hit is fairly minimal and more importantly, it actually generates the right answer:
$ cargo run --release --bin 16-pressurinator 2 data/16-test.txt
Step2 { fuel: 26, per_tick_flow: 0, data: Schedule { agent: 0, distance: 2, target: "JJ" } }
Step2 { fuel: 26, per_tick_flow: 0, data: Schedule { agent: 1, distance: 1, target: "DD" } }
Step2 { fuel: 26, per_tick_flow: 0, data: AdvanceTime { ticks: 1 } }
Step2 { fuel: 25, per_tick_flow: 0, data: EnableTick { activations: [(1, "DD")] } }
Step2 { fuel: 24, per_tick_flow: 20, data: Schedule { agent: 1, distance: 4, target: "HH" } }
Step2 { fuel: 24, per_tick_flow: 20, data: EnableTick { activations: [(0, "JJ")] } }
Step2 { fuel: 23, per_tick_flow: 41, data: Schedule { agent: 0, distance: 3, target: "BB" } }
Step2 { fuel: 23, per_tick_flow: 41, data: AdvanceTime { ticks: 3 } }
Step2 { fuel: 20, per_tick_flow: 41, data: EnableTick { activations: [(0, "BB"), (1, "HH")] } }
Step2 { fuel: 19, per_tick_flow: 76, data: Schedule { agent: 0, distance: 1, target: "CC" } }
Step2 { fuel: 19, per_tick_flow: 76, data: Schedule { agent: 1, distance: 3, target: "EE" } }
Step2 { fuel: 19, per_tick_flow: 76, data: AdvanceTime { ticks: 1 } }
Step2 { fuel: 18, per_tick_flow: 76, data: EnableTick { activations: [(0, "CC")] } }
Step2 { fuel: 17, per_tick_flow: 78, data: Schedule { agent: 0, distance: 5, target: "HH" } }
Step2 { fuel: 17, per_tick_flow: 78, data: AdvanceTime { ticks: 1 } }
Step2 { fuel: 16, per_tick_flow: 78, data: EnableTick { activations: [(1, "EE")] } }
Step2 { fuel: 15, per_tick_flow: 81, data: Schedule { agent: 1, distance: 4, target: "JJ" } }
Step2 { fuel: 15, per_tick_flow: 81, data: AdvanceTime { ticks: 3 } }
Step2 { fuel: 12, per_tick_flow: 81, data: EnableTick { activations: [(0, "HH")] } }
Step2 { fuel: 11, per_tick_flow: 81, data: Schedule { agent: 0, distance: 6, target: "BB" } }
Step2 { fuel: 11, per_tick_flow: 81, data: EnableTick { activations: [(1, "JJ")] } }
Step2 { fuel: 10, per_tick_flow: 81, data: Schedule { agent: 1, distance: 7, target: "HH" } }
Step2 { fuel: 10, per_tick_flow: 81, data: AdvanceTime { ticks: 5 } }
Step2 { fuel: 5, per_tick_flow: 81, data: EnableTick { activations: [(0, "BB")] } }
Step2 { fuel: 4, per_tick_flow: 81, data: Schedule { agent: 0, distance: 3, target: "JJ" } }
Step2 { fuel: 4, per_tick_flow: 81, data: AdvanceTime { ticks: 1 } }
Step2 { fuel: 3, per_tick_flow: 81, data: EnableTick { activations: [(1, "HH")] } }
Step2 { fuel: 2, per_tick_flow: 81, data: DoNothing }
1707
took 251.897791ms
Okay. That’s great! Let’s try it on the ~6 times larger (with factorially worse run time) input.
Problems with memory (?)
$ cargo run --release --bin 16-pressurinator 2 data/16.txt
...
Compiling aoc2022 v0.1.0 (/Users/jp/Projects/advent-of-code/2022)
Finished release [optimized] target(s) in 37.41s
Running `target/release/16-pressurinator 2 data/16.txt`
zsh: killed cargo run --release --bin 16-pressurinator 2 data/16.txt
Yeah… that’s not good. It would run for several minutes and just crash. I googled, tried cargo clean, tried a new browser, tried it in debug mode (that took longer and still crashed). On branch suggested zld might cause this issue, but I’m not using it. I thought perhaps a Rust bug…
$ rustc --version
rustc 1.64.0
$ rustup update
info: syncing channel updates for 'stable-aarch64-apple-darwin'
info: latest update on 2022-12-15, rust version 1.66.0 (69f9c33d7 2022-12-12)
...
info: checking for self-updates
stable-aarch64-apple-darwin updated - rustc 1.66.0 (69f9c33d7 2022-12-12) (from rustc 1.62.1 (e092d0b6b 2022-07-16))
Unfortunately that didn’t help. Either. So … what’s going on?
Improving memory usage
Well, remember how I talked about Vector sharing structs and saving me a bunch of memory? Well, in practice… I’m either using it wrong or don’t quite understand it.
Exhibit A:

Yup. That’s the program (in release mode!) using 45 GB of RAM. I’m writing most of this on an M1 Mac Mini… with 16 GB of RAM. So most of that is in swap. It actually made it up to 60 GB of RAM before the OS killed it off.
Great.
So, how do we fix it?
Well, there are two big parts of the recursive calls that I should be able to optimize:
- The
im::Vectorofenabledvalves - The
im::Vectorofagents
For the first, it’s a Vector<bool>. I should be able to pack all of those values (even 59 of them) into a single 64-bit integer. Enter bitvec. I’ve given up on not using third party crates, there are some things that (after hours and hours of working on this) I don’t want to reimplement just now.
For the conversion, we kick it off with this instead:
// Init the agents and kick the recursive function off
let cave = Rc::new(self);
let (total_flow, steps) = recur(
cave.clone(),
Rc::new(RefCell::new(HashMap::new())),
Vector::from(vec![State::new(cave.clone().indexes[&location]); agents]),
fuel,
BitVec::from_vec(vec![0; cave.clone().size]),
);
Then we need to change the various cache types and function signatures to expect this value and finally change the enabled[agent.index] = true to enabled.set(agent.index, true). After that, it just works. We’re still cloneing it, but it’s a 64-bit integer being copied. Much better.
Next up, agents. This doesn’t change much. Really for two, it’s 4 usize values (an index and ttl for each). So instead of Vector, I just switched to Vec. It turns out it’s optimized all to heck and cheap enough to copy those two bytes rather than all the extra bookkeeping from Vector.
All of that done and…
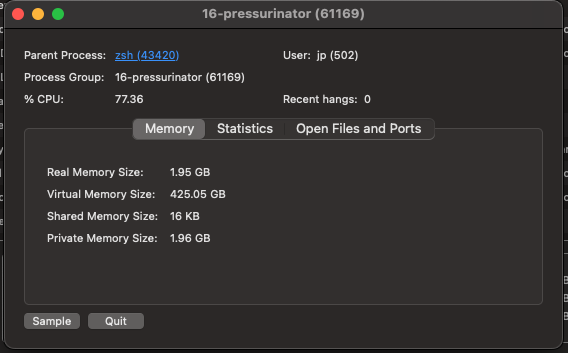
It’s still taking up a chunk of my machine… but it’s better!
I’m … not 100% sure what the difference between Real Memory Size and Virtual Memory Size is there. I think Real is what it’s actually using and Virtual is what it theoretically has access to? In that case, we should be good to go.
Improving runtime
It’s still very slow. So… how can we do better? Well, remember how I said that in both the EnableTick and AdvanceTime states there was only one possibility? Well branching (in this case) is expensive and takes even more memory. So let’s see if we can clean everything up into a single case.
impl Cave {
// The same simulation but with multiple agents
fn max_flow_multi(
self,
location: String,
fuel: usize,
agents: usize,
) -> (usize, Vec<StepMulti>) {
type CacheKey = (Vec<State>, usize, BitVec);
type CacheValue = (usize, Vec<StepMulti>);
// Main recursive function with multiple agents
// cave and cache still don't change (other than to cache values)
// agents is an im::Vector of agent states, can be any number (even 1)
// - this contains the next index
// - plus a new value ttl which is how long it will take the agent to get to the index
// fuel is how long the simulation can still run
// enabled is the map of which flows are enabled
fn recur(
cave: Rc<Cave>,
cache: Rc<RefCell<HashMap<CacheKey, CacheValue>>>,
agents: Vec<State>,
fuel: usize,
enabled: BitVec,
) -> CacheValue {
// Cache based on the state of all agents/fuel/enabled
let cache_key = (agents.clone(), fuel, enabled.clone());
if cache.borrow().contains_key(&cache_key) {
return cache.borrow_mut()[&cache_key].clone();
}
// Calculate flow per tick (even if we won't actually tick)
let per_tick_flow = cave
.clone()
.flow_rates
.iter()
.zip(enabled.clone().iter())
.filter_map(|(f, c)| if *c { Some(*f) } else { None })
.sum::<usize>();
// Base case: try doing nothing for the rest of the simulation
let mut result = (
fuel * per_tick_flow,
vec![StepMulti {
fuel,
per_tick_flow,
data: StepMultiData::DoNothing,
}],
);
// Once all useful flows are active, allow moving to anywhere
// This fixes a previous bug where the first free agent would claim the last valve even it was further away
let potential_enabled = cave
.clone()
.flow_rates
.iter()
.zip(enabled.clone())
.filter_map(|(f, e)| if *f > 0 && !e { Some(true) } else { None })
.count();
// If the TTL of any agent is 0, schedule it's next move
// This doesn't advance time
if let Some((i, agent)) = agents.clone().iter().enumerate().find(|(_, a)| a.ttl == 0) {
for next_index in 0..cave.clone().size {
// Not allowed to move to the same target as any other agent
// Can only move to an already enabled valve if we're in the end state
if agents.clone().iter().any(|a| next_index == a.index)
|| (potential_enabled >= agents.len() && enabled[next_index])
|| cave.clone().flow_rates[next_index] == 0
{
continue;
}
// Check that we have enough fuel to move there
let d = cave.clone().distances[[agent.index, next_index]];
if d + 1 > fuel {
continue;
}
// Update the agent with where it's going + how long to get there and enable
let mut new_agents = agents.clone();
new_agents[i] = State {
index: next_index,
ttl: d + 1,
};
// Make the recursive call and record that we did
let mut sub_result = recur(
cave.clone(),
cache.clone(),
new_agents,
fuel,
enabled.clone(),
);
sub_result.1.push(StepMulti {
fuel,
per_tick_flow,
data: StepMultiData::Schedule {
agent: i,
distance: d,
target: cave.clone().names[next_index].clone(),
},
});
// If making this call was better than the current result (of do nothing)
// Use it instead
result = result.max(sub_result);
}
}
// Otherwise, advance by the ttl of the lowest agent
else {
let mut activations = Vec::new();
// Find time until the agent(s) that will finish moving soonest
let ticks = agents
.clone()
.iter()
.min_by(|a, b| a.ttl.cmp(&b.ttl))
.expect("must have at least one agent")
.ttl;
// Enable any flows for agents with TTL=0 at the end of this move
let mut next_enabled = enabled.clone();
for (i, agent) in agents.clone().iter().enumerate() {
if agent.ttl == ticks {
next_enabled.set(agent.index, true);
activations.push((i, cave.clone().names[agent.index].clone()));
}
}
// Update all agents (including those that will go to 0)
let mut next_agents = agents.clone();
for (i, agent) in agents.clone().iter().enumerate() {
next_agents[i] = agent.tick(ticks);
}
// Make the recursive call
let mut sub_result = recur(
cave.clone(),
cache.clone(),
next_agents,
fuel - ticks,
next_enabled,
);
// Update flow by that many ticks + record what step we took
// As always, if this result is better than nothing, record it
sub_result.0 += ticks * per_tick_flow;
sub_result.1.push(StepMulti {
fuel,
per_tick_flow,
data: StepMultiData::AdvanceTime { ticks, activations },
});
result = result.max(sub_result);
}
// Memoize the result and finally return
cache.borrow_mut().insert(cache_key, result.clone());
result
}
// Init the agents and kick the recursive function off
let cave = Rc::new(self);
let (total_flow, steps) = recur(
cave.clone(),
Rc::new(RefCell::new(HashMap::new())),
vec![State::new(cave.clone().indexes[&location]); agents],
fuel,
BitVec::from_vec(vec![0; cave.clone().size]),
);
// Because we're using Vec, the steps end up in reverse order
(total_flow, steps.into_iter().rev().collect::<Vec<_>>())
}
}
Basically I got rid of the relatively annoying ttl = 1 state and instead handle that and the advance in the same tick. It’s a bit cleaner code and a bit quicker.
To be continued…
Unfortunately, a bit quicker is still way too slow. At this point, I’ve been working on this problem for quite a while, so I’m going to go ahead and move on to another. I’ll let it run overnight to get an answer (if it does), but I still do want to try something better.
I think one option would be to give up on perfect and instead try a heuristic approach like simulated annealing. It won’t be able to guarantee me the perfect answer, but I expect it will find one good enough in far less time.
Like I said, to be continued…
Certainly one of the most interesting problems so far this year!
Let it run! (Edit, Dec 20)
So the good news is:
cargo run --release --bin 16-pressurinator 2 data/16.txt
Finished release [optimized] target(s) in 0.15s
Running `target/release/16-pressurinator 2 data/16.txt`
StepMulti { fuel: 26, per_tick_flow: 0, data: Schedule { agent: 0, distance: 2, target: "CA" } }
StepMulti { fuel: 26, per_tick_flow: 0, data: Schedule { agent: 1, distance: 2, target: "TU" } }
StepMulti { fuel: 26, per_tick_flow: 0, data: AdvanceTime { ticks: 3, activations: [(0, "CA"), (1, "TU")] } }
StepMulti { fuel: 23, per_tick_flow: 24, data: Schedule { agent: 0, distance: 3, target: "FP" } }
StepMulti { fuel: 23, per_tick_flow: 24, data: Schedule { agent: 1, distance: 2, target: "UK" } }
StepMulti { fuel: 23, per_tick_flow: 24, data: AdvanceTime { ticks: 3, activations: [(1, "UK")] } }
StepMulti { fuel: 20, per_tick_flow: 42, data: Schedule { agent: 1, distance: 3, target: "EK" } }
StepMulti { fuel: 20, per_tick_flow: 42, data: AdvanceTime { ticks: 1, activations: [(0, "FP")] } }
StepMulti { fuel: 19, per_tick_flow: 47, data: Schedule { agent: 0, distance: 2, target: "YH" } }
StepMulti { fuel: 19, per_tick_flow: 47, data: AdvanceTime { ticks: 3, activations: [(0, "YH"), (1, "EK")] } }
StepMulti { fuel: 16, per_tick_flow: 87, data: Schedule { agent: 0, distance: 2, target: "UX" } }
StepMulti { fuel: 16, per_tick_flow: 87, data: Schedule { agent: 1, distance: 3, target: "GW" } }
StepMulti { fuel: 16, per_tick_flow: 87, data: AdvanceTime { ticks: 3, activations: [(0, "UX")] } }
StepMulti { fuel: 13, per_tick_flow: 110, data: Schedule { agent: 0, distance: 2, target: "AR" } }
StepMulti { fuel: 13, per_tick_flow: 110, data: AdvanceTime { ticks: 1, activations: [(1, "GW")] } }
StepMulti { fuel: 12, per_tick_flow: 126, data: Schedule { agent: 1, distance: 2, target: "JT" } }
StepMulti { fuel: 12, per_tick_flow: 126, data: AdvanceTime { ticks: 2, activations: [(0, "AR")] } }
StepMulti { fuel: 10, per_tick_flow: 146, data: Schedule { agent: 0, distance: 8, target: "JF" } }
StepMulti { fuel: 10, per_tick_flow: 146, data: AdvanceTime { ticks: 1, activations: [(1, "JT")] } }
StepMulti { fuel: 9, per_tick_flow: 168, data: DoNothing }
2536
took 9366.7117265s
2.5 hours, but it finished!
The bad news is… that’s apparently not actually my answer. But apparently:
That’s not the right answer; your answer is too low. Curiously, it’s the right answer for someone else; you might be logged in to the wrong account or just unlucky.
That’s kind of hilarious.
Back to the drawing board!
Queues to the rescue (Edit 3, Dec 20)
Okay, I’ve rewritten the code
impl Cave {
fn max_flow_multi(self, start: String, fuel: usize, agents: usize) -> (usize, Vec<Vec<usize>>) {
let mut queue = Vec::new();
let start_path = vec![self.indexes[start.as_str()]];
queue.push((0, vec![fuel; agents], vec![start_path.clone(); agents]));
let start = Instant::now();
let mut tick = Instant::now();
let mut count = 0;
let mut best = (0, vec![start_path.clone(); agents]);
while !queue.is_empty() {
let (pressure, enabled, fuels, paths) = queue.pop().unwrap();
count += 1;
seen.insert((fuels.clone(), paths.clone()));
if pressure > best.0 {
best = (pressure, paths.clone());
}
// For each path and each next node to visit:
// - check if the node is worth visiting (no duplicates, has flow, can reach)
// - if so, add that as a possibility
for (path_i, path) in paths.iter().enumerate() {
for next_i in 0..self.size {
let d = self.distances[[*path.last().unwrap(), next_i]];
if paths.iter().any(|path| path.contains(&next_i))
|| self.flow_rates[next_i] == 0
|| d + 1 > fuels[path_i]
{
continue;
}
let mut new_paths = paths.clone();
new_paths[path_i].push(next_i);
let mut new_fuels = fuels.clone();
new_fuels[path_i] -= d + 1;
queue.push((
pressure + (fuels[path_i] - d - 1) * self.flow_rates[next_i],
new_fuels,
new_paths,
));
}
}
}
best
}
}
And… we’ve got a working solution! (With test output enabled).
$ AOC16_PRINT_PROGRESS=true cargo run --release --bin 16-pressurinator 2 data/16.txt
new best: pressure=198, extra fuel=[26, 22], paths: [2=AA]; [2=AA, 57=ZJ]
new best: pressure=498, extra fuel=[26, 15], paths: [2=AA]; [2=AA, 57=ZJ, 56=AR]
...
new best: pressure=2278, extra fuel=[9, 1], paths: [2=AA, 46=TU, 39=UK, 19=EK, 42=GW, 6=JT]; [2=AA, 57=ZJ, 56=AR, 53=YH, 10=UX, 49=LE]
new best: pressure=2284, extra fuel=[9, 0], paths: [2=AA, 46=TU, 39=UK, 19=EK, 42=GW, 6=JT]; [2=AA, 57=ZJ, 56=AR, 53=YH, 10=UX, 48=FP, 49=LE]
After 5s, examined 4629791 states, pruned 0, seen skipped 0, 115 in queue
new best: pressure=2293, extra fuel=[9, 1], paths: [2=AA, 46=TU, 39=UK, 19=EK, 42=GW, 6=JT]; [2=AA, 57=ZJ, 56=AR, 10=UX, 53=YH, 52=DM, 48=FP]
new best: pressure=2296, extra fuel=[9, 2], paths: [2=AA, 46=TU, 39=UK, 19=EK, 42=GW, 6=JT]; [2=AA, 57=ZJ, 56=AR, 10=UX, 53=YH, 52=DM, 45=BO]
new best: pressure=2312, extra fuel=[9, 3], paths: [2=AA, 46=TU, 39=UK, 19=EK, 42=GW, 6=JT]; [2=AA, 57=ZJ, 56=AR, 10=UX, 53=YH, 49=LE]
new best: pressure=2328, extra fuel=[9, 2], paths: [2=AA, 46=TU, 39=UK, 19=EK, 42=GW, 6=JT]; [2=AA, 57=ZJ, 56=AR, 10=UX, 53=YH, 48=FP, 49=LE]
After 10s, examined 9140709 states, pruned 0, seen skipped 0, 108 in queue
After 15s, examined 13547476 states, pruned 0, seen skipped 0, 113 in queue
After 20s, examined 17649720 states, pruned 0, seen skipped 0, 116 in queue
After 25s, examined 21287456 states, pruned 0, seen skipped 0, 107 in queue
After 30s, examined 25016730 states, pruned 0, seen skipped 0, 130 in queue
new best: pressure=2418, extra fuel=[9, 1], paths: [2=AA, 46=TU, 39=UK, 19=EK, 42=GW, 6=JT]; [2=AA, 57=ZJ, 53=YH, 56=AR, 10=UX, 52=DM, 48=FP]
new best: pressure=2421, extra fuel=[9, 2], paths: [2=AA, 46=TU, 39=UK, 19=EK, 42=GW, 6=JT]; [2=AA, 57=ZJ, 53=YH, 56=AR, 10=UX, 52=DM, 45=BO]
new best: pressure=2437, extra fuel=[9, 3], paths: [2=AA, 46=TU, 39=UK, 19=EK, 42=GW, 6=JT]; [2=AA, 57=ZJ, 53=YH, 56=AR, 10=UX, 49=LE]
new best: pressure=2453, extra fuel=[9, 2], paths: [2=AA, 46=TU, 39=UK, 19=EK, 42=GW, 6=JT]; [2=AA, 57=ZJ, 53=YH, 56=AR, 10=UX, 48=FP, 49=LE]
After 35s, examined 28908560 states, pruned 0, seen skipped 0, 132 in queue
After 40s, examined 32720919 states, pruned 0, seen skipped 0, 107 in queue
After 45s, examined 36323227 states, pruned 0, seen skipped 0, 120 in queue
After 50s, examined 39991418 states, pruned 0, seen skipped 0, 109 in queue
new best: pressure=2460, extra fuel=[9, 0], paths: [2=AA, 46=TU, 39=UK, 19=EK, 42=GW, 6=JT]; [2=AA, 57=ZJ, 53=YH, 10=UX, 56=AR, 49=LE, 48=FP]
new best: pressure=2481, extra fuel=[9, 3], paths: [2=AA, 46=TU, 39=UK, 19=EK, 42=GW, 6=JT]; [2=AA, 57=ZJ, 53=YH, 10=UX, 56=AR, 48=FP, 49=LE]
After 55s, examined 44030437 states, pruned 0, seen skipped 0, 118 in queue
After 60s, examined 48168693 states, pruned 0, seen skipped 0, 106 in queue
...
After 1610s, examined 1404049877 states, pruned 0, seen skipped 0, 101 in queue
After 1615s, examined 1408789336 states, pruned 0, seen skipped 0, 125 in queue
new best: pressure=2491, extra fuel=[9, 0], paths: [2=AA, 46=TU, 39=UK, 19=EK, 42=GW, 6=JT]; [2=AA, 53=YH, 56=AR, 10=UX, 57=ZJ, 40=CA, 38=JF]
new best: pressure=2496, extra fuel=[9, 2], paths: [2=AA, 46=TU, 39=UK, 19=EK, 42=GW, 6=JT]; [2=AA, 53=YH, 56=AR, 10=UX, 52=DM, 57=ZJ, 40=CA]
new best: pressure=2499, extra fuel=[9, 2], paths: [2=AA, 46=TU, 39=UK, 19=EK, 42=GW, 6=JT]; [2=AA, 53=YH, 56=AR, 10=UX, 49=LE, 40=CA]
new best: pressure=2503, extra fuel=[9, 2], paths: [2=AA, 46=TU, 39=UK, 19=EK, 42=GW, 6=JT]; [2=AA, 53=YH, 56=AR, 10=UX, 49=LE, 38=JF]
new best: pressure=2517, extra fuel=[9, 1], paths: [2=AA, 46=TU, 39=UK, 19=EK, 42=GW, 6=JT]; [2=AA, 53=YH, 56=AR, 10=UX, 48=FP, 49=LE, 40=CA]
new best: pressure=2519, extra fuel=[9, 1], paths: [2=AA, 46=TU, 39=UK, 19=EK, 42=GW, 6=JT]; [2=AA, 53=YH, 56=AR, 10=UX, 48=FP, 49=LE, 38=JF]
new best: pressure=2529, extra fuel=[9, 2], paths: [2=AA, 46=TU, 39=UK, 19=EK, 42=GW, 6=JT]; [2=AA, 53=YH, 56=AR, 10=UX, 48=FP, 40=CA, 38=JF]
After 1620s, examined 1413401408 states, pruned 0, seen skipped 0, 117 in queue
After 1625s, examined 1418009194 states, pruned 0, seen skipped 0, 114 in queue
...
After 1790s, examined 1570622231 states, pruned 0, seen skipped 0, 88 in queue
After 1795s, examined 1575400277 states, pruned 0, seen skipped 0, 90 in queue
new best: pressure=2535, extra fuel=[9, 0], paths: [2=AA, 46=TU, 39=UK, 19=EK, 42=GW, 6=JT]; [2=AA, 53=YH, 10=UX, 56=AR, 49=LE, 40=CA, 38=JF]
new best: pressure=2541, extra fuel=[9, 0], paths: [2=AA, 46=TU, 39=UK, 19=EK, 42=GW, 6=JT]; [2=AA, 53=YH, 10=UX, 56=AR, 49=LE, 38=JF, 40=CA]
new best: pressure=2558, extra fuel=[9, 2], paths: [2=AA, 46=TU, 39=UK, 19=EK, 42=GW, 6=JT]; [2=AA, 53=YH, 10=UX, 56=AR, 48=FP, 49=LE, 40=CA]
new best: pressure=2562, extra fuel=[9, 2], paths: [2=AA, 46=TU, 39=UK, 19=EK, 42=GW, 6=JT]; [2=AA, 53=YH, 10=UX, 56=AR, 48=FP, 49=LE, 38=JF]
new best: pressure=2571, extra fuel=[9, 3], paths: [2=AA, 46=TU, 39=UK, 19=EK, 42=GW, 6=JT]; [2=AA, 53=YH, 10=UX, 56=AR, 48=FP, 40=CA, 38=JF]
After 1800s, examined 1579723741 states, pruned 0, seen skipped 0, 122 in queue
After 1805s, examined 1584409877 states, pruned 0, seen skipped 0, 108 in queue
...
After 2400s, examined 2141415612 states, pruned 0, seen skipped 0, 97 in queue
After 2405s, examined 2145881260 states, pruned 0, seen skipped 0, 98 in queue
After 2410s, examined -2144238898 states, pruned 0, seen skipped 0, 100 in queue
After 2415s, examined -2139331679 states, pruned 0, seen skipped 0, 99 in queue
// 'lol. Oops. I examined more than i32::MAX states :smile:'
// 'Since it takes ~45 minutes to even get to that state, I am not going to fix it now'
...
// 'Here we go again, back in the positives!'
After 5055s, examined 188736513 states, pruned 0, seen skipped 0, 89 in queue
After 5060s, examined 192958619 states, pruned 0, seen skipped 0, 108 in queue
// 'After almost 1.5 hours, found the best answer'
new best: pressure=2582, extra fuel=[3, 9], paths: [2=AA, 40=CA, 53=YH, 10=UX, 56=AR, 48=FP, 49=LE]; [2=AA, 46=TU, 39=UK, 19=EK, 42=GW, 6=JT]
// 'But we are not done yet! What if something even *better* is out there...'
After 5065s, examined 197635931 states, pruned 0, seen skipped 0, 97 in queue
After 5070s, examined 201800520 states, pruned 0, seen skipped 0, 95 in queue
It’s the same basic solution as the single agent priority queue, albeit with multiple agents. Rather than previous solutions where I tried to keep track of where each agent was in the simulation and step through all at once, I’m doing a bit more of a brute force solution.
To generate new states: For each agent, consider each possible next step add them to the stack. This means that we’ll look into the solutions where one agent takes all of the moves and the other takes none up through even splits.
Let’s see if we can make it better.
Optimization: remaining_best_case (Edit 4, Dec 21)
After a nice sleep, I have a few optimizations that I think we can use. First, we are keeping track of the best scene solution as we go. So, similar to how A* works, if we can given an upper bound for the best we can possibly do… and even that isn’t good enough to match what we already have, then there’s no point in looking further down that path.
To do that, for each state that we pop off the queue:
let enable_prune_optimization = env::var("AOC16_OPT_PRUNE").is_ok();
let mut prune_count = 0;
let mut best = (0, vec![start_path.clone(); agents]);
while !queue.is_empty() {
let (pressure, fuels, paths) = queue.pop().unwrap();
if pressure > best.0 {
best = (pressure, paths.clone());
}
if enable_prune_optimization {
// Calculate the best case remaining flow and stop if we can't hit it
// For each node:
let remaining_best_case = self
.flow_rates
.iter()
.enumerate()
.map(|(i, f)| {
// If it's already on, ignore it
if paths.iter().any(|path| path.contains(&i)) {
0
} else {
// Otherwise, for each agent, find the agent that would be best
// This is defined as the flow rate * the fuel left after moving to that node
// Take the best case here
// This will over estimate, since it assumes each node can go to all nodes at once
paths
.iter()
.enumerate()
.map(|(pi, p)| {
let d = self.distances[[*p.last().unwrap(), i]];
if d + 1 <= fuels[pi] {
f * (fuels[pi] - d - 1)
} else {
0
}
})
.max()
.unwrap()
}
})
.sum::<usize>();
// If even the best case isn't good enough, don't consider any more cases on this branch
if pressure + remaining_best_case < best.0 {
prune_count += 1;
continue;
}
}
...
}
I went through a few different iterations of this. At first, I only took whichever of the agents had the most fuel left and multiplied that by the total maximum flow left. That certainly gave an upper bound. But this instead gives a much tighter one by:
- For each valve that is not enabled:
- For each agent:
- Calculate the flow that would be generated if that agent went immediately to turn this on
- Take the maximum value from each agent
- For each agent:
- Sum these values
This does given an impossible value, because it essentially is sending each agent to all of the nodes it’s closest to at the very same time, but in practice, this is a good balance of a good upper bound (the answer will be no higher than this) and quick enough to calculate.
Putting it into practice:
$ AOC16_PRINT_PROGRESS=true AOC16_OPT_PRUNE=true cargo run --release --bin 16-pressurinator 2 data/16.txt
new best: pressure=198, extra fuel=[26, 22], paths: [2=AA]; [2=AA, 57=ZJ]
new best: pressure=498, extra fuel=[26, 15], paths: [2=AA]; [2=AA, 57=ZJ, 56=AR]
...
new best: pressure=2562, extra fuel=[9, 2], paths: [2=AA, 46=TU, 39=UK, 19=EK, 42=GW, 6=JT]; [2=AA, 53=YH, 10=UX, 56=AR, 48=FP, 49=LE, 38=JF]
new best: pressure=2571, extra fuel=[9, 3], paths: [2=AA, 46=TU, 39=UK, 19=EK, 42=GW, 6=JT]; [2=AA, 53=YH, 10=UX, 56=AR, 48=FP, 40=CA, 38=JF]
After 5s, examined 6149307 states, pruned 5505822, 89 in queue
new best: pressure=2582, extra fuel=[3, 9], paths: [2=AA, 40=CA, 53=YH, 10=UX, 56=AR, 48=FP, 49=LE]; [2=AA, 46=TU, 39=UK, 19=EK, 42=GW, 6=JT]
After 10s, examined 12418080 states, pruned 11143082, 96 in queue
After 15s, examined 18347378 states, pruned 16449571, 106 in queue
After 20s, examined 24461538 states, pruned 21933515, 79 in queue
After 25s, examined 30916652 states, pruned 27741938, 98 in queue
After 30s, examined 37409349 states, pruned 33567664, 65 in queue
After 35s, examined 43763543 states, pruned 39260996, 57 in queue
[Final] After 39.43722s, examined 49025754 states, pruned 43992685, 0 in queue
2582
took 39.439913125s
So rather than having to go through billions of states, I only had to calculate 49 million of them and managed to prune another 4.3 million directly. Not so bad!
Especially when you look at the RAM usage:

That’s almost hilarious given that we started at ~60 GB…
And we’re under a minute, so we could just end now… but I think there’s one more trick, since we’re using so little ram.
Optimization: seen_skip (Edit 4, Dec 21)
Last trick: We aren’t caching the results any more, but there are still cases where we end up looking into the same state more than once. If that happens, then all the branches from there (that aren’t otherwise pruned) will be checked more than once.
So why don’t we keep a simple HashSet that holds all of the states we’ve seen. As a bonus, since we’re not storing the pressure going back but rather as we go, we don’t have to cache based on that. Just the fuels and paths:
let enable_seen_optimization = env::var("AOC16_OPT_SEEN").is_ok();
let mut seen = HashSet::new();
let mut seen_skip_count = 0;
let mut best = (0, vec![start_path.clone(); agents]);
while !queue.is_empty() {
let (pressure, fuels, paths) = queue.pop().unwrap();
count += 1;
if enable_seen_optimization {
seen.insert((fuels.clone(), paths.clone()));
}
if pressure > best.0 {
best = (pressure, paths.clone());
}
// For each path and each next node to visit:
// - check if the node is worth visiting (no duplicates, has flow, can reach)
// - if so, add that as a possibility
for (path_i, path) in paths.iter().enumerate() {
for next_i in 0..self.size {
let d = self.distances[[*path.last().unwrap(), next_i]];
if paths.iter().any(|path| path.contains(&next_i))
|| self.flow_rates[next_i] == 0
|| d + 1 > fuels[path_i]
{
continue;
}
let mut new_paths = paths.clone();
new_paths[path_i].push(next_i);
let mut new_fuels = fuels.clone();
new_fuels[path_i] -= d + 1;
if enable_seen_optimization {
if seen.contains(&(new_fuels.clone(), new_paths.clone())) {
seen_skip_count += 1;
continue;
}
}
queue.push((
pressure + (fuels[path_i] - d - 1) * self.flow_rates[next_i],
new_fuels,
new_paths,
));
}
}
}
It’s certainly much easier code!
And let it run:
$ AOC16_PRINT_PROGRESS=true AOC16_OPT_SEEN=true cargo run --release --bin 16-pressurinator 2 data/16.txt
...
new best: pressure=2437, extra fuel=[9, 3], paths: [2=AA, 46=TU, 39=UK, 19=EK, 42=GW, 6=JT]; [2=AA, 57=ZJ, 53=YH, 56=AR, 10=UX, 49=LE]
new best: pressure=2453, extra fuel=[9, 2], paths: [2=AA, 46=TU, 39=UK, 19=EK, 42=GW, 6=JT]; [2=AA, 57=ZJ, 53=YH, 56=AR, 10=UX, 48=FP, 49=LE]
After 5s, examined 1835009 states, pruned 0, seen skipped 1753459, 89 in queue
new best: pressure=2460, extra fuel=[9, 0], paths: [2=AA, 46=TU, 39=UK, 19=EK, 42=GW, 6=JT]; [2=AA, 57=ZJ, 53=YH, 10=UX, 56=AR, 49=LE, 48=FP]
new best: pressure=2481, extra fuel=[9, 3], paths: [2=AA, 46=TU, 39=UK, 19=EK, 42=GW, 6=JT]; [2=AA, 57=ZJ, 53=YH, 10=UX, 56=AR, 48=FP, 49=LE]
After 10s, examined 3676455 states, pruned 0, seen skipped 3595186, 136 in queue
After 15s, examined 6101511 states, pruned 0, seen skipped 5995146, 125 in queue
...
After 61s, examined 18760775 states, pruned 0, seen skipped 18588534, 102 in queue
After 66s, examined 20841264 states, pruned 0, seen skipped 20436456, 91 in queue
new best: pressure=2491, extra fuel=[9, 0], paths: [2=AA, 46=TU, 39=UK, 19=EK, 42=GW, 6=JT]; [2=AA, 53=YH, 56=AR, 10=UX, 57=ZJ, 40=CA, 38=JF]
new best: pressure=2496, extra fuel=[9, 2], paths: [2=AA, 46=TU, 39=UK, 19=EK, 42=GW, 6=JT]; [2=AA, 53=YH, 56=AR, 10=UX, 52=DM, 57=ZJ, 40=CA]
After 71s, examined 22839969 states, pruned 0, seen skipped 22619589, 110 in queue
new best: pressure=2499, extra fuel=[9, 2], paths: [2=AA, 46=TU, 39=UK, 19=EK, 42=GW, 6=JT]; [2=AA, 53=YH, 56=AR, 10=UX, 49=LE, 40=CA]
new best: pressure=2503, extra fuel=[9, 2], paths: [2=AA, 46=TU, 39=UK, 19=EK, 42=GW, 6=JT]; [2=AA, 53=YH, 56=AR, 10=UX, 49=LE, 38=JF]
new best: pressure=2517, extra fuel=[9, 1], paths: [2=AA, 46=TU, 39=UK, 19=EK, 42=GW, 6=JT]; [2=AA, 53=YH, 56=AR, 10=UX, 48=FP, 49=LE, 40=CA]
new best: pressure=2519, extra fuel=[9, 1], paths: [2=AA, 46=TU, 39=UK, 19=EK, 42=GW, 6=JT]; [2=AA, 53=YH, 56=AR, 10=UX, 48=FP, 49=LE, 38=JF]
new best: pressure=2529, extra fuel=[9, 2], paths: [2=AA, 46=TU, 39=UK, 19=EK, 42=GW, 6=JT]; [2=AA, 53=YH, 56=AR, 10=UX, 48=FP, 40=CA, 38=JF]
After 76s, examined 24932281 states, pruned 0, seen skipped 24794833, 106 in queue
After 81s, examined 27003104 states, pruned 0, seen skipped 26778550, 101 in queue
After 86s, examined 28932748 states, pruned 0, seen skipped 28657995, 106 in queue
new best: pressure=2535, extra fuel=[9, 0], paths: [2=AA, 46=TU, 39=UK, 19=EK, 42=GW, 6=JT]; [2=AA, 53=YH, 10=UX, 56=AR, 49=LE, 40=CA, 38=JF]
new best: pressure=2541, extra fuel=[9, 0], paths: [2=AA, 46=TU, 39=UK, 19=EK, 42=GW, 6=JT]; [2=AA, 53=YH, 10=UX, 56=AR, 49=LE, 38=JF, 40=CA]
new best: pressure=2558, extra fuel=[9, 2], paths: [2=AA, 46=TU, 39=UK, 19=EK, 42=GW, 6=JT]; [2=AA, 53=YH, 10=UX, 56=AR, 48=FP, 49=LE, 40=CA]
new best: pressure=2562, extra fuel=[9, 2], paths: [2=AA, 46=TU, 39=UK, 19=EK, 42=GW, 6=JT]; [2=AA, 53=YH, 10=UX, 56=AR, 48=FP, 49=LE, 38=JF]
new best: pressure=2571, extra fuel=[9, 3], paths: [2=AA, 46=TU, 39=UK, 19=EK, 42=GW, 6=JT]; [2=AA, 53=YH, 10=UX, 56=AR, 48=FP, 40=CA, 38=JF]
After 254s, examined 29360129 states, pruned 0, seen skipped 29071617, 93 in queue
After 259s, examined 30150593 states, pruned 0, seen skipped 30046623, 125 in queue
...
After 1130s, examined 77331070 states, pruned 0, seen skipped 76852978, 111 in queue
After 1135s, examined 78015975 states, pruned 0, seen skipped 77488650, 91 in queue
new best: pressure=2582, extra fuel=[3, 9], paths: [2=AA, 40=CA, 53=YH, 10=UX, 56=AR, 48=FP, 49=LE]; [2=AA, 46=TU, 39=UK, 19=EK, 42=GW, 6=JT]
After 1140s, examined 78565285 states, pruned 0, seen skipped 78053151, 72 in queue
After 1145s, examined 79133865 states, pruned 0, seen skipped 78708279, 101 in queue
...
After 5556s, examined 153816325 states, pruned 0, seen skipped 153169389, 62 in queue
After 5561s, examined 154058540 states, pruned 0, seen skipped 153651769, 22 in queue
[Final] After 5564.9927s, examined 154092423 states, pruned 0, seen skipped 153988506, 0 in queue
2582
took 5565.1033s
Oof. Well… that’s not great. Mostly because it’s eating 10s of GB of RAM again. But that’s not actually the real benefit.
On the plus side, we’re examining 154 million states and explicitly skipping another 154 million (amusing those are so close, mirror symmetry between the agents? I didn’t actually account for that…). So there’s something here, we just don’t have enough RAM to do it.
But what really shines is if you turn on both at once:
$ AOC16_PRINT_PROGRESS=true AOC16_OPT_PRUNE=true AOC16_OPT_SEEN=true cargo run --release --bin 16-pressurinator 2 data/16.txt
new best: pressure=198, extra fuel=[26, 22], paths: [2=AA]; [2=AA, 57=ZJ]
new best: pressure=498, extra fuel=[26, 15], paths: [2=AA]; [2=AA, 57=ZJ, 56=AR]
...
new best: pressure=2571, extra fuel=[9, 3], paths: [2=AA, 46=TU, 39=UK, 19=EK, 42=GW, 6=JT]; [2=AA, 53=YH, 10=UX, 56=AR, 48=FP, 40=CA, 38=JF]
new best: pressure=2582, extra fuel=[3, 9], paths: [2=AA, 40=CA, 53=YH, 10=UX, 56=AR, 48=FP, 49=LE]; [2=AA, 46=TU, 39=UK, 19=EK, 42=GW, 6=JT]
After 5s, examined 3409689 states, pruned 3046753, seen skipped 395207, 73 in queue
After 10s, examined 5778507 states, pruned 5155304, seen skipped 774332, 47 in queue
[Final] After 10.216912s, examined 5871899 states, pruned 5233589, seen skipped 847204, 0 in queue
2582
took 12.029340416s
Now that’s what we’re talking about. By pruning branches and skipping states we’ve already seen, we’ve managed to get the runtime down to only 10 seconds, another 4x speedup over just pruning. And this time, we did end up going through 5.8 million states, pruning and skipping another ~6 million. Now that’s what I’m talking about!
It does use a decent amount of RAM, but < 8GB, which well fits within my machine. Always tradeoffs there.
At this point, I think I’m finally ready to give this one a rest. :)
Threading
I did actually write up a threaded version using Arc<Mutex<...>> for most of the data structures. It’s neat… but not any faster. You can check out the code on github if you’re interested.
Graphviz visualizations
Well, almost. One fun thing I did while I was working through this problem:
Turned the maps into Graphviz, using GraphvizOnline to render them (although I do have it installed, having the live output was nice). Essentially, I copied the input, and for each line like this:
Valve BB has flow rate=13; tunnels lead to valves CC, AA
I generated:
graph {
// If flow rate = 0
AA [style=dashed]
...
// If flow rate > 0, includes flow rate
BB [shape=doublecircle, label="BB\n13"]
...
// Edges (doubled edges are because I generated both)
BB -- CC, AA
...
}
The full map looks even cooler:
I kind of want to animate the agents and flow over each step… but I’ve already spent entirely too much time on this problem. 😄
Performance
I’ve done so many iterations of this at this point… here’s a table:
| Part | Algorithm | Opt: Prune | Opt: Skip | Time | RAM | Examined | Pruned | Skipped |
|---|---|---|---|---|---|---|---|---|
| 1 | recursive | [1] | [1] | 175ms | [2] | – | – | – |
| 1 | PriorityQueue | [1] | [1] | 100ms | [2] | – | – | – |
| 1 | stack (Vec) | [1] | [1] | 72ms | [2] | – | – | – |
| 2 | stack (Vec) | no | no | >2 hr | < 10 MB | > 8B | – | – |
| 2 | stack (Vec) | no | yes | 1.5 hr | 30 GB | 154M | – | 154M |
| 2 | stack (Vec) | yes | no | 39 s | < 10 MB | 49M | 4.3M | – |
| 2 | stack (Vec) | yes | yes | 12 s | < 8 GB | 5.8M | 5.2M | 800k |
Notes:
- Not much point in optimizing these, they’re fast enough already.
- Likewise, they finish so fast, I don’t actually see how much RAM it’s using.
- This value actually wrapped the
i32I was using. Twice.
Not too bad!