AoC 2017 Day 21: Fractal Expander

Source: Fractal Art

Part 1: Start with an input image made of . and # pixels. For n iterations, break the image into blocks:
If the current size is even, break the image into 2x2 chunks and replace each with a 3x3 chunk
If the current size is odd, break the image into 3x3 chunks and replace each with a 4x4 chunk
The replacement rules will be specified in the following format (example is a 3x3 -> 4x4 rule):
.#./..#/### => #..#/..../..../#..#  
In that example, replace this:
.#.
..#
###
With this:
#..#
....
....
#..#
Any rotation or reflection of a chunk can be used to match the input of a replacement rule.
After n = 18 iterations, how many # pixels are there?

This is quite a problem. One of the first things that we have to deal with is what we’re going to use for our data format for each step. I settled on keeping a single 1D string. It will always have a perfect square for the size, so we can always take a square root to render it as an actual square.

With that, we can work on expanding the image for each step.

First, we have to break apart the data into either 2x2 or 3x3 blocks:

def blocks(data):
    '''
    Convert data into blocks.

    If data has an even number of elements, return 2x2 blocks.
    If it has an odd number, return 3x3 blocks.

    Assume data is a perfect square.
    '''

    if len(data) % 2 == 0:
        block_size = 2
    else:
        block_size = 3

    data_row_width = int(math.sqrt(len(data)))
    grid_size = data_row_width // block_size

    for grid_y in range(grid_size):
        for grid_x in range(grid_size):
            yield ''.join(
                data[data_row_width * block_size * grid_y + data_row_width * block_y + block_size * grid_x + block_x]
                for block_y in range(block_size)
                for block_x in range(block_size)
            )

The idea is that we have two nested grids. The larger grid is specified by grid_size and contains many 2x2 or 3x3 blocks within it. The smaller grid is always either 2x2 or 3x3 and within each block. With those two bits of information, we can calculate the index within the original data string to extract for each block. I think this is relatively readable, although if anyone has a way this could be made better, I’d love to see it. It’s mostly just a weird problem to work on.

Next, we want to take those blocks and expand them. To do that though, we need to be able to determine what the 8 possible rotations/reflections of a given square are:

def rotations(block):
    '''Yield the 8 rotations/flips of a block.'''

    size = int(math.sqrt(len(block)))

    for i in range(2):
        for j in range(4):
            yield block

            # Rotate 90 degrees clockwise
            block = ''.join(
                block[(size - x - 1) * size + y]
                for y in range(size)
                for x in range(size)
            )

        # Flip vertically
        block = ''.join(
            block[(size - y - 1) * size + x]
            for y in range(size)
            for x in range(size)
        )

This doesn’t remove duplicates, but it’s only 8 per block. If it matters, we can come back to this later (perhaps using a set to only return each unique string once?).

With that, we have the ability to expand either a single block or to use that to expand an entire grid full of blocks:

def expand_block(block):
    '''Expand a single block.'''

    for rotation in rotations(block):
        if rotation in rules:
            return rules[rotation]

    raise Exception(f'Unable to expand {block}')

def expand(data):
    '''Expand an entire grid.'''

    return deblock([
        expand_block(block)
        for block in blocks(data)
    ])

Rules are loaded from our input file. It’s just a map of .# etc (either 4 or 9 long) to the same form output (either 9 or 16 long).

And finally, we’ll take the expanded blocks and turn them back into the single long string. Another potential optimization would be to keep them in the unexpanded format¹.

def deblock(data):
    '''
    Inverse of the above, turn a list of blocks back into data.
    '''

    block_size = int(math.sqrt(len(data[0])))
    grid_size = int(math.sqrt(len(data)))

    return ''.join(
        data[grid_y * grid_size + grid_x][block_y * block_size + block_x]
        for grid_y in range(grid_size)
        for block_y in range(block_size)
        for grid_x in range(grid_size)
        for block_x in range(block_size)
    )

It’s basically the inverse of the blocks function above, albeit a bit easier yet to read.

Now that we have all that, the actual expansion function is pretty clean:

data = lib.param('state').replace('/', '')
for round in range(lib.param('iterations')):
    data = expand(data)

print(render_block(data).count('#'))

Part 2: Do the same thing for 18 iterations.

No code changes. Just wait a bit longer¹. It’s quick enough though:

$ python3 run-all.py day-21

day-21  python3 fractal-expander.py input.txt --iterations 5    0.11855697631835938     133
day-21  python3 fractal-expander.py input.txt --iterations 18   22.69156503677368       2221990

Instead, let’s render some pretty pictures. Using the generate_image function from 2015 / used in day 14, we can render any given block as an image:

def render_image(data, filename):
    '''Render a block as an image (assumes # is black and . is white).'''

    size = int(math.sqrt(len(data)))

    def generate_pixel(x, y):
        g = 0 if data[y * size + x] == '#' else 255
        return (g, g, g)

    lib.generate_image(size, size, generate_pixel).save(filename)

If we do that, we can see the images at any particular step:

Part 2: After 18 Iterations (Click for full size)

Or we can animate the whole thing as it expands using ImageMagick again:

$ convert -delay 10 -interpolate Nearest -filter point -resize 324x324 frame-*.png fractal.gif

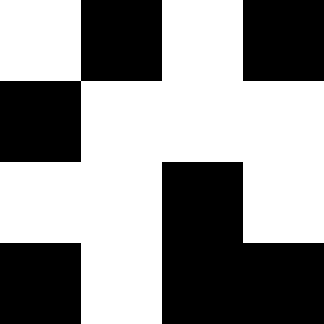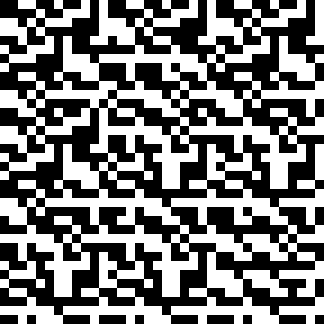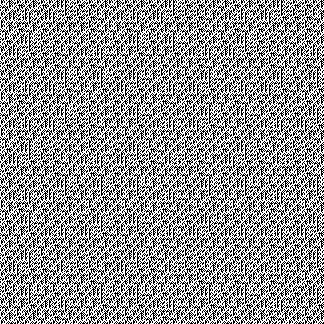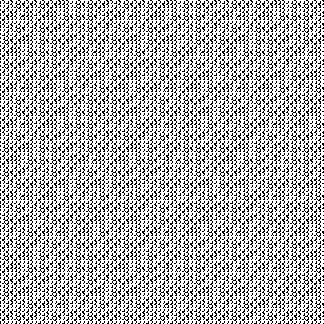
In fact, we don’t actually have to generate the entire image at all to determine how many pixels are on. We only have to recursively calculate each ‘superpixel’ going down layers. We could cache each possible result and save quite a lot of time doing this. On the other hand, it only takes ~20 seconds to calculate part 2, so 🤷. ↩︎ ↩︎