A few days ago an interesting article came across my RSS feeds: It’s All Greek (or Chinese or Spanish or…) to Me. Basically, in English, when you’re confused, you’ll often say ‘It’s all Greek to me’. It turns out that man (if not all) languages around the world have a similar saying, but the target varies. Luckily, Wikipedia has a lovely page about it: Greek to me.
When I posted the link to Facebook, I got a quick question: are there any cycles? While one could just scan through the document, it would be a lot more interesting (at least to me!) if you could do it automatically. Let’s toss together a quick script to do it.
First thing we need: a way to get the content of the Wikipedia page. Python is great for this, with requests to grab the page and BeautifulSoup to process it:
content = requests.get('https://en.wikipedia.org/wiki/Greek_to_me').text
soup = bs4.BeautifulSoup(content)
table = soup.find('table', {'class': 'wikitable sortable'})
pairs = collections.defaultdict(set)
for row in table.findAll('tr'):
cols = row.findAll('td')
if not cols:
continue
if len(cols) == 5:
srcs = [src.strip() for src in cols[0].text.split(',')]
dsts = [dst.strip() for dst in cols[-1].text.split(',')]
for i, dst in enumerate(dsts):
dsts[i] = re.sub(r'[\[(].*?[\])]', '', dst)
for src in srcs:
if ' ' in src: continue
for dst in dsts:
if ' ' in dst: continue
pairs[src].add(dst)
Basically, we download the page. Then we go through each of the rows (tr). Skip any rows without column elements (td) as that’s probably the header, otherwise, pull them out. The first column (index 0) is the language with the idiom (English in the example) while the last column (index -1) is the target (Greek). There’s one caveat though, that sometimes the table uses a rowspan when one source can have multiple targets but is only listed once. We check that by only changing the srcs when there are 5 columns.
Parse through all of that and what do you have?
>>> import pprint
>>> pprint.pprint(dict(pairs))
{u'': set([]),
u'Afrikaans': set([u'Greek']),
u'Albanian': set([u'Chinese']),
u'Arabic': set([u'Chinese', u'Garshuni']),
...
u'Vietnamese': set([u'Cambodian']),
u'Volap\xfck': set([]),
u'Yiddish': set([u'Aramaic'])}
Exactly what I was looking for. Okay, next step. Find any cycles in the graph. This is straight forward enough by performing a depth first search:
def cycle(node, seen):
for neighbor in pairs[node]:
new_seen = seen + [neighbor]
if neighbor in seen:
yield new_seen[new_seen.index(neighbor):]
else:
for recur in cycle(neighbor, new_seen):
yield recur
The basic idea is to make a generator that returns each cycle as it finds it. It does so by search down each branch, maintaining a list of all nodes it has seen. If it sees the same node twice, that’s a cycle. Otherwise, try all of the neighbors. We avoid infinite loops since there’s a guaranteed base case to the recursion: seen is always one bigger on each step and it’s maximum size is the number of nodes in the graph.
So how does it work?
>>> for result in cycle('English', ['English']):
... print result
...
['English', u'Greek', u'Chinese', u'English']
['English', u'Greek', u'Turkish', u'Arabic', u'Chinese', u'English']
['English', u'Greek', u'Turkish', u'French', u'Chinese', u'English']
['English', u'Greek', u'Turkish', u'French', u'Hebrew', u'Chinese', u'English']
['English', u'Dutch', u'Chinese', u'English']
Neat! We’ve already found 5 cycles that involve English alone. But how many cycles are there all together? For that, we need a way to determine if a cycle is actually unique. If you have the cycles A -> B -> C -> A, that’s the same as B -> C -> A -> B. You can do this by putting the cycles in lexical order (so that the ‘smallest’ element in the cycle is first).
def reorder(cycle):
if cycle[0] == cycle[-1]:
cycle = cycle[1:]
smallest = min(cycle)
for el in list(cycle):
if el == smallest:
break
else:
cycle = cycle[1:] + [cycle[0]]
return cycle
It also is smart enough that if we pass it a list with the first and last node the same (as we will), it trims that off automatically.
>>> reorder(['A', 'B', 'C', 'A'])
['A', 'B', 'C']
>>> reorder(['B', 'C', 'A', 'B'])
['A', 'B', 'C']
Bam. So we use that and a set to keep track of what we’ve seen:
>>> seen = set()
>>> for src in pairs.keys():
... for result in cycle(src, [src]):
... result = reorder(result)
... if not str(result) in seen:
... print(result)
... seen.add(str(result))
...
[u'Chinese', u'English', u'Greek']
[u'Chinese', u'English', u'Dutch']
[u'Arabic', u'Chinese', u'English', u'Greek', u'Turkish']
[u'Chinese', u'English', u'Greek', u'Turkish', u'French']
[u'Chinese', u'English', u'Greek', u'Turkish', u'French', u'Hebrew']
Huh. So they all go through English. I didn’t actually expect that. :) Still, it’s cool to be able to unify them like that.
Okay, one last trick. Let’s visualize them. Luckily, there’s a nice Python interface for graphviz that we can use:
# --- Render a nice graph ---
g = graphviz.Digraph()
for src in pairs.keys():
for dst in pairs[src]:
g.edge(src, dst)
g.graph_attr['overlap'] = 'false'
g.graph_attr['splines'] = 'true'
g.format = 'png'
g.engine = 'neato'
g.render('greek-to-me')
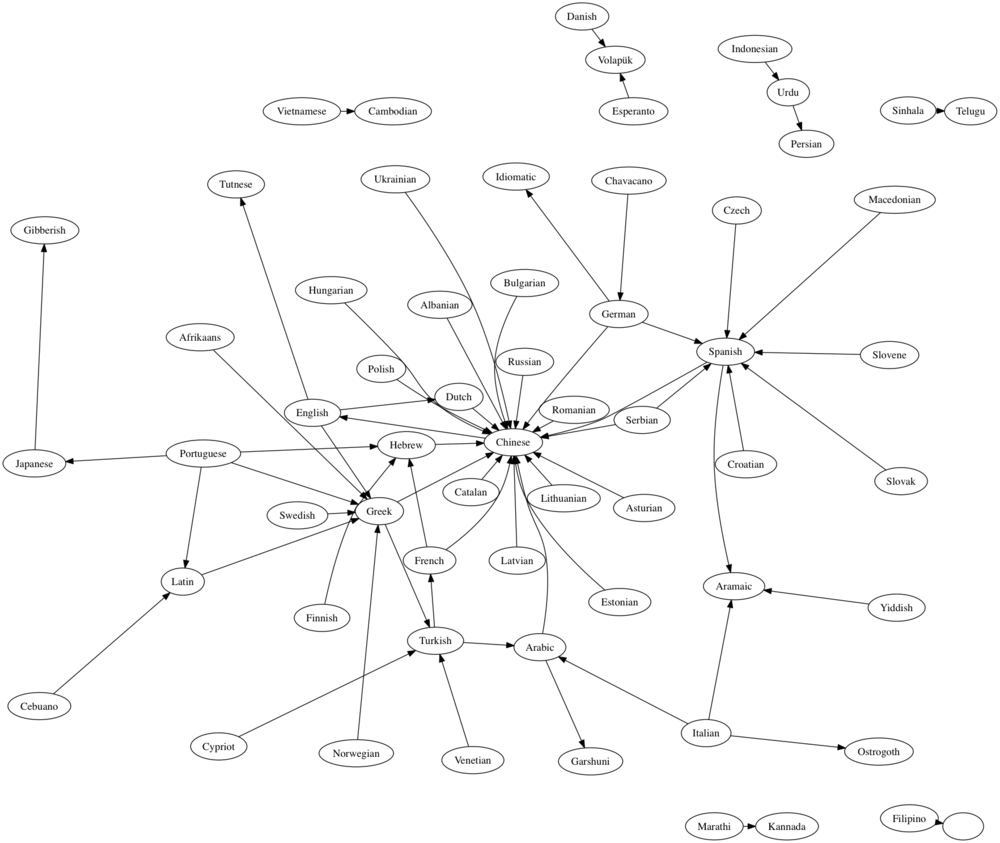
Awesome.
It’s not the easiest thing in the world to read, but if you look carefully you can pick out a few interesting things. Let’s tweak it a bit to color nodes if and only if they have both an inward edge and an outward one:
for src in pairs.keys():
# Does this node lead to another
has_out = pairs[src]
# Does any node lead to this one
has_in = False
for dst in pairs.keys():
if src in pairs[dst]:
has_in = True
break
# If both, color it
if has_out and has_in:
g.node(src, color = 'blue')
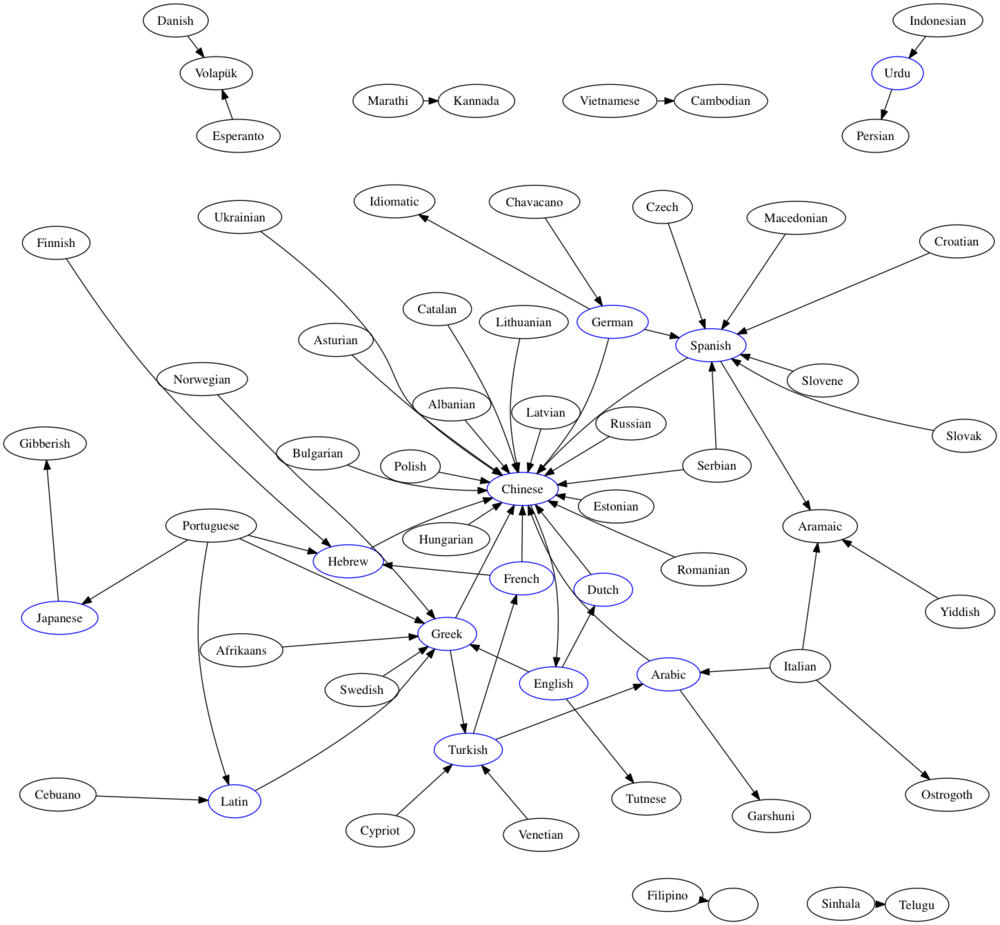
That’s a little better, all of the nodes in any cycle are in there. Let’s go ahead and show all of the edges in any cycle:
# Get all edges that are part of a cycle
cycle_edges = set()
for cycle in cycles:
for src, dst in zip(cycle, cycle[1:]):
cycle_edges.add((src, dst))
cycle_edges.add((cycle[-1], cycle[0]))
for src in pairs.keys():
for dst in pairs[src]:
if (src, dst) in cycle_edges:
g.edge(src, dst, color = 'blue')
else:
g.edge(src, dst)
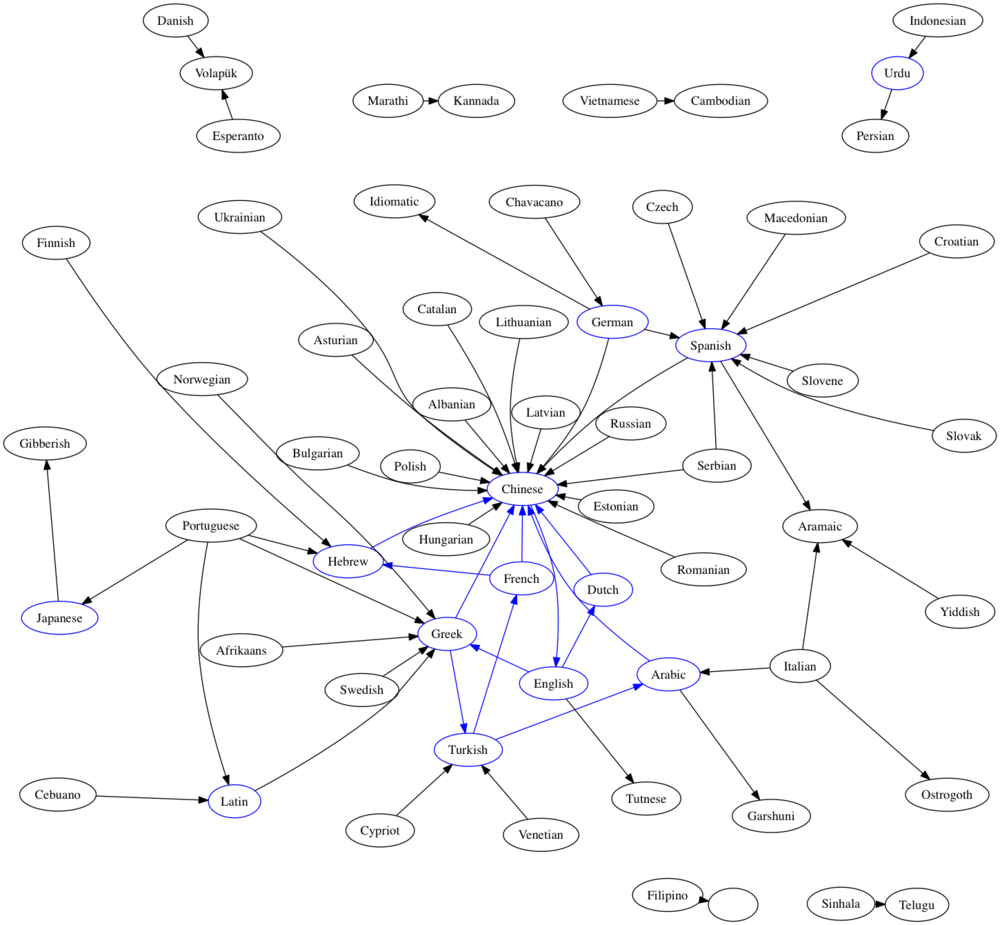
So they’re all in that pocket. If I had a few more minutes, I could show all of the cycles as different colors, but that gets complicated in that many re-use the same paths. So it goes.
If you’d like to see / run the code, you can grab it from GitHub: greek-to-me.py