It’s been a while1, but I’m back. Today’s post is inspired by a post from /r/dailyprogrammer almost a month ago now: Challenge #183 [Intermediate] Edge Matching Tile Puzzle. Basically, we’re going to solve puzzles like this:


If you look carefully, the tiles are the same between the two, although they might be rotated.
Okay, let’s start at the beginning. How are we going to represent a puzzle? Well, let’s go with the same basic idea that was described in the original post: sets of four letters (in the order north, east, south, west), one for each tile. Furthermore, the letters represent color. Originally CMYK for cyan, magenta, yellow, and black, but we’ll also add RGB for red, green, and blue (it’s easy enough to add colors). Next, we’ll use upper case and lower case letters in order to represent the two halves of a matching image.
So take the unsolved image above:

The first tile would be described as cymK for three circles and one rectangle. Continuing on, the entire puzzle would be:
'("cymK" "KyCy" "ymkc" "mkYc" "MycK" "mCkY" "cmKY" "KYmC" "McMk")
Now we’ll want two helper functions:
; Insert an item into the given location in a list
(define (insert-at ls item x)
(for/list ([i (in-naturals)]
[el (in-list ls)])
(if (= x i) item el)))
; Return a list of all rotated versions of a string
(define (rotations str)
(for/list ([i (in-range (string-length str))])
(string-append (substring str i) (substring str 0 i))))
Specifically, the first function allows us to insert a tile into a specified location in a list, while the second returns all possible rotations of our four character string. All around, things are going to be a little inefficient because we’re working with lists rather than directly accessing something like a vector, but since the size of the puzzle is so small, the cost for these functions will be relatively cheap (especially compared to the crazy number of possible orderings of the tiles).
Okay, with that, we actually have enough of a framework to work out our solution. The basic plan of attack will be very much the same as when we worked on the N Queens Puzzle. Place each piece in order, backtracking as soon as we see a valid solution. This way we can cut out huge swaths of the potential solution space.
; Solve a puzzle by ordering pieces so that they match
(define (solve puzzle)
; Start with an empty solution space (all null) and a list of pieces to place
(let loop ([solution (make-list (length puzzle) "\0\0\0\0")]
[to-place puzzle]
[index 0])
(cond
; If we've filled in all of the pieces, we have a solution
[(= index (length puzzle))
solution]
; Otherwise, try each piece, only recurring for those that fit
; Return the first that solves the puzzle from here,
; by recursion this will be a full solution
[else
(for*/first ([next-item (in-list to-place)]
[next-item-rotated (in-list (rotations next-item))]
[next-puzzle (in-value (insert-at solution
next-item-rotated
index))]
#:when (valid? next-puzzle)
[recur (in-value (loop next-puzzle
(remove next-item to-place)
(+ index 1)))]
#:when recur)
recur)])))
Basically there are two interesting parts: the let loop and the for*/first block. The main loop is the primary bit of the recursion. At any particular step, we have the solution that we’ve built thus far. We’ll start with all \0 strings (which we’ll special case in valid?) and then fill in puzzle pieces one at a time. to-place will hold the pieces we’ve yet to place. The index is used primarily to insert new pieces at the proper location.
Next, we have the for*/first loop. This is designed to clean up the search, basically by returning the first recursion that makes it through all of the lists and conditionals. Specifically, we’re going to do all of the following:
- Loop through all remaining pieces to place as
next-item - For each piece, try each rotation in turn
- Generate the
next-puzzleby inserting that piece - Check that the new insertion is
valid? - Recur with the newly placed piece removed
- If there’s a valid solution, continue to the body of the loop (and thus return, since we’re looking for the
first)
All that combines (with the power of recursion!) to solve the puzzle:
> (solve '("cymK" "KyCy" "ymkc"
"mkYc" "MycK" "mCkY"
"cmKY" "KYmC" "McMk"))
'("cymK" "mCkY" "ymkc"
"McMk" "KYmC" "KyCy"
"mkYc" "MycK" "cmKY")
Of course that’s a little hard to see what in the world is going on. Let’s write a few functions using Racket’s pict
library. First, a parameter
to control how large each tile will be and a pair of functions to decode the letters into colors / shapes:
(define current-tile-size (make-parameter 50))
(define (char->color c)
(case c
[(#\R #\r) "red"]
[(#\G #\g) "green"]
[(#\B #\b) "blue"]
[(#\C #\c) "cyan"]
[(#\M #\m) "magenta"]
[(#\Y #\y) "yellow"]
[(#\K #\k) "black"]
[else "white"]))
(define (char->shape c)
(case c
[(#\R #\G #\B #\C #\M #\Y #\K) filled-rectangle]
[(#\r #\g #\b #\c #\m #\y #\k) filled-ellipse]
[(#\null) (λ _ (filled-rectangle 0 0))]))
With those, we can render an individual tile:
; Render a single tile given a four character specifier
; Order is top, right, bottom, left
; Colors are cyan, magenta, yellow, red, green, blue, black (k for black)
; Uppercase are square, lowercase are circular
(define (render-tile tile)
(match-define (list top right bottom left) (string->list tile))
; Size of the individual images
(define quad-size (quotient (current-tile-size) 3))
; Offsets for pinning, zero/half/full size adjusted for quad size
(define zs (- (quotient quad-size 2)))
(define hs (- (quotient (current-tile-size) 2) (quotient quad-size 2)))
(define fs (- (current-tile-size) (quotient quad-size 2)))
; Helper function to render a specific shape of the specific color
(define (shape c)
(colorize ((char->shape c) quad-size quad-size)
(char->color c)))
; Construct the image by layering each of the four sides on the base
(let* ([pict (rectangle (current-tile-size) (current-tile-size))]
[pict (pin-under pict hs zs (shape top))]
[pict (pin-under pict fs hs (shape right))]
[pict (pin-under pict hs fs (shape bottom))]
[pict [pin-under pict zs hs (shape left)]])
(clip pict)))
One part that took a bit here was getting the zs, hs, and fs functions correct. Since coordinates are based on the top left corner of each subimage, we need to correctly offset by half of the image sizes for each of the halfway points. Also, make sure you use the clip
function. It will look fine with just a single tile if you do not use it, but once you start merging them… Strange things happen.
Demo time:
> (render-tile "cymK")
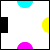
Nice!
Next, we can combine the picts into a single larger pict:
; Render a puzzle of multiple tiles
; Puzzles are assumed to be square
(define (render puzzle)
(define width (integer-sqrt (length puzzle)))
(define tiles
(for/list ([y (in-range width)])
(for/list ([x (in-range width)])
(render-tile (list-ref puzzle (+ x (* y width)))))))
(define rows
(map (λ (row) (apply (curry hc-append -1) row)) tiles))
(apply (curry vc-append -1) rows))
Bam:
> (render (solve '("cymK" "KyCy" "ymkc"
"mkYc" "MycK" "mCkY"
"cmKY" "KYmC" "McMk")))

Neat! We can try it on larger puzzles as well:
…
Okay, that takes a really long time. Perhaps a 4x4 with more colors (more colors is actually easier to solve since there are less valid placements for each tile):
> (define p4x4 (random-puzzle 4 #:colors 7))
> p4x4
'("yyMY" "mCKM" "Cgrr" "BMMy"
"MrYB" "mGYK" "BRyG" "gRmc"
"KCCm" "cyby" "mYbY" "BMcB"
"Bmbm" "kbrr" "MkYc" "ybGY")
> (render p4x4)

> (define p4x4-solution (solve p4x4))
> p4x4-solution
'("rCgr" "BBMc" "YmYb" "yBMM"
"GBRy" "mBmb" "ycyb" "mKCC"
"rkbr" "MmCK" "YyyM" "cMkY"
"BMrY" "cgRm" "YybG" "KmGY")
> (render p4x4-solution)

Shiny. 😄
For those interested, here’s how I generated random puzzles:
; Generate random puzzles
(define (random-puzzle size #:colors [colors 4])
; Generate n+1 intersections (including those off the edges)
; Each value is the top left corner of a tile with the right then down edge
(define intersections
(for/list ([y (in-range (+ size 1))])
(for/list ([x (in-range (+ size 1))])
(for/list ([which (in-list '(right down))])
(list (string-ref "CMYKRGB" (random (min colors 7)))
(if (= 0 (random 2)) 'normal 'inverse))))))
(define (@ x y w invert?)
(match-define (list char mode)
(list-ref (list-ref (list-ref intersections y) x)
(if (eq? w 'right) 0 1)))
((if (xor invert? (eq? mode 'inverse))
char-downcase
identity)
char))
; Fill out the tiles
(shuffle
(for*/list ([y (in-range size)]
[x (in-range size)])
(string (@ x y 'right #f)
(@ (+ x 1) y 'down #f)
(@ x (+ y 1) 'right #t)
(@ x y 'down #t)))))
And that’s it. Surprisingly simple2 to solve, a little more to render. I love problems like this. 😄
If you really want to go off the deep end though and, go download the full source from GitHub (tile-puzzles.rkt). Therein lies solutions for using simulated annealing or genetic algorithms in an effort to solve the problem more heurisitically, but neither is working particularly well as of yet. If you want to take one of those and finish it up, I’d love to see it.