Oops, turns out I haven’t had a post in a good long while. Before it gets even longer, I figure that I should take one off my backlog and just write it up, even if it is a little on the shorter side.

Today’s post was inspired by this post on /r/dailyprogrammer a month ago today: Challenge #178 [Hard] Regular Expression Fractals. The basic idea is that you are going to take a rectangular region and divide it into four quadrants, again and again, recording the path as you go (images from that post):

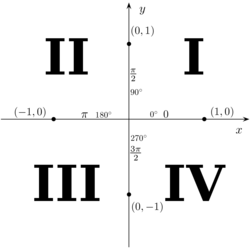
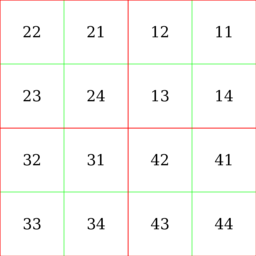
At the end, each point in the image will have a ‘path’ of decisions that got you there, making a string of the numbers 1, 2, 3, and 4.

How does that translate into code?

; Generate a fractal by matching a recursive path into an image
(define (regex-fractal regex size)
  (flomap->bitmap
   (build-flomap*
    3 size size
    (λ (x y)
      (let loop ([t 0] [l 0] [s size] [path ""])
        (cond
          ; If we're at the last level, white, otherwise black
          [(<= s 1)
           (cond
             [(regexp-match regex path) '#(1 1 1)]
             [else                      '#(0 0 0)])]
          ; Otherwise, divide the region into four subregions
          ; Recur into whichever our current pixel is in
          [else
           (define s/2 (quotient s 2))
           (define x-mid (+ l s/2))
           (define y-mid (+ t s/2))
           (loop
            (if (< y y-mid) t y-mid)
            (if (< x x-mid) l x-mid)
            s/2
            (~a path
                (match (list (< y y-mid) (< x x-mid))
                  ['(#t #t) 2]
                  ['(#t #f) 1]
                  ['(#f #t) 3]
                  ['(#f #f) 4])))]))))))

That’s actually pretty close to a lot of the fractal code we’ve been writing recently. And it generates some pretty cool images already:

> (regex-fractal #px"(13|31|24|42)" 256)

But we can do a little better than that. Let’s parameterize a few things:

(define current-size     (make-parameter 64))
(define current-coloring (make-parameter (thunk* '#(1 1 1))))
(define current-mode     (make-parameter 'short))

Specifically, we’ll pull the size out, but also add two more parameters. A mode to short circuit (so that as soon as the pattern matches, return, rather than calculating the entire depth of the image) and another to color the pixel based on a specific match. As an example coloring, consider this:

; Get the maximum path length; useful for making gradients
(define (size->path-length size)
  (inexact->exact (floor (/ (log size) (log 2)))))

; Color a pixel based on how long of a match group we have
(define (color-by-length m)
  (define l (string-length (car m)))
  (define p (size->path-length (current-size)))
  (if (= l p)
      '#(1 1 1)
      (vector
       (if (>= (length m) 3) (/ (string-length (list-ref m 2)) p) 0)
       (if (>= (length m) 2) (/ (string-length (list-ref m 1)) p) 0)
       (if (>= (length m) 4) (/ (string-length (list-ref m 3)) p) 0))))

Now, let’s take another example, one where the matching group must contain a 1. But now, color based on how much of the path is before the one:

(parameterize ([current-size 256]
               [current-coloring color-by-length]
               [current-mode 'short])
  (regex-fractal #px"(.*)1"))

Very cool.

After that, I just collected and made up a bunch of colorings and regular expressions and generate all of the images. Check the full source on GitHub for details, but basically I have three colorings: a default white only, the length based coloring above, and another which matches the most common color in a match. Then I have about two dozen regular expression.

Then I wrote a quick loop that will generate all images in both modes (short circuiting and long), with all three colorings. It’s a lot of images… Here are some of my favorites:

(demo "test256" 256)

First, a basic Sierpinski triangle 1:

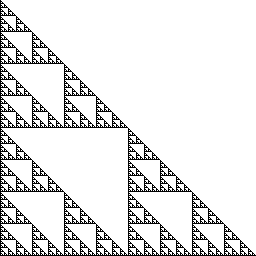
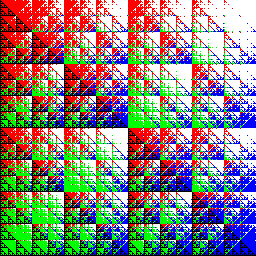
But if you turn on most common color, you see that each color sticks to it’s own color (a pattern we’ll see oft repeated):

What’s even more interesting is when you switch to ‘short mode’. Since we’ll stop recurring as soon as we see a 1, you get blocks rather than each individual pixel colored:

Next, four corners. Basically, look for repeated patterns of a single digit: ((.)(\\2*)). That should mean that we go out to the four corners, each with its own color:

Next, split the region into left and right halves, by checking if a 1 or 2 appears first: ^[34]*2(.*). If it’s a 2, mark it, if it’s a 1, do not.

Next, a nice jagged change on the original Sierpinski, match anything with either a 1 or a 2 (or both): (12)

Or, similarly, make two Sierpinskis by matching patterns where there’s both a 1 and a 2: (1.*2|2.*1):

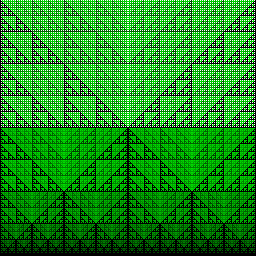
Next, match patterns where all 1s (if any) occur before all 2s: ^[34]*[134]*[34]*[234]*[34]*$

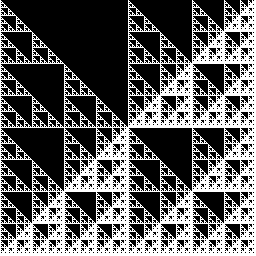
Or you can invert the Sierpinski triangle by making sure there are no ones at all: ^[^1]*$

Or go really crazy and do some math. For example, finding all sequences with an even sum: ^(2|4|[13][24]*[13])*$

Next, we have a few from the comments on the original post.

Some nice curls: [13][24][^1][^2][^3][^4]

Patterns where you have the same pattern repeated at least three times, but with other random bits in between: (.)\\1..\\1

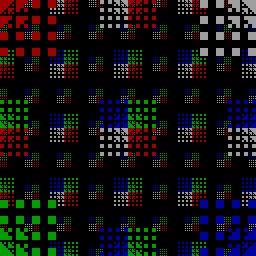
Or you can draw some nice boxes: (?:13|31)(.*)

A nice recursive outline (reminds me of the Fractal Invaders): ^(1[124]|2[14]|4[12]|31)*$

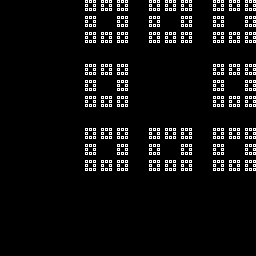
Figure eights: ^(?:..)*(?:[13][13]|[24][24])((?:..)*)$

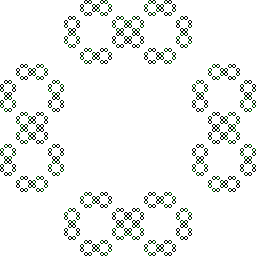
And finally, some nice diagonal lines, by making sure the top left/bottom right are before the top right/bottom left: ^[13]*[24]*$:

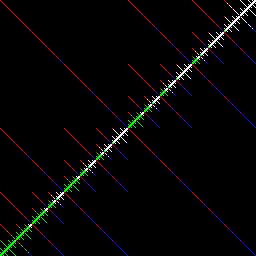
And there you have it. Any other awesome patterns you come up with? Share them below. I’d love to see them.

As always, the full source is available on GitHub if you’d like to play with it: regex-fractal.rkt