First we had Procedural Invaders. Then we used them fill up space with Fractal Invaders. But we’re not quite done yet! This time, let’s mix things up a bit and make Invader Fractals.

Specifically, here’s the algorithm that we want to use to build an invader fractal:
- Generate an invader
- Within that image:
- For each white pixel, stop
- For each black pixel, recur with a smaller invader
- Once the invader is small enough, stop recurring
Sounds straight forward enough, but what does that look like in code?
; An invader fractal is nested 5x5 2d vectors, each element is either
; #t/#f - a white/black region
; a recursive 5x5 structure
(define (make-invader-fractal depth)
(let loop ([depth depth])
(define invader (flomap-add-margin (procedural-invader (random 32768)) 1))
(for/vector ([x (in-range 7)])
(for/vector ([y (in-range 7)])
(if (> 0.5 (flomap-ref invader 0 x y))
(if (<= depth 1)
#t
(loop (- depth 1)))
#f)))))
That’s actually a lot more concise than I first expected. In the end, we get exactly that nice nested structure we’re looking for:
> (make-invader-fractal 2)
'#(#(#f #f #f #f #f #f #f)
#(#f
#(#(#f #f #f #f #f #f #f)
#(#f #f #t #f #t #f #f)
#(#f #f #f #f #t #f #f)
#(#f #t #t #f #f #t #f)
#(#f #f #f #f #t #f #f)
#(#f #f #t #f #t #f #f)
#(#f #f #f #f #f #f #f))
#f
#(#(#f #f #f #f #f #f #f)
#(#f #t #t #f #t #t #f)
#(#f #f #t #t #f #f #f)
#(#f #f #f #t #t #f #f)
#(#f #f #t #t #f #f #f)
#(#f #t #t #f #t #t #f)
#(#f #f #f #f #f #f #f))
#f
...
#f
#f
#f)
#(#f #f #f #f #f #f #f))
>
We could probably do away with representing the margins (the outermost layer is always going to be #f), but at the moment it makes the code easier to reason about.
Okay, next we need the rendering function:
; Render an invader fractal as defined above
; Crop off the margin on the outmost layer
; Final size will be 5*7^{depth-1}
(define (render-invader-fractal fi)
(define depth
(let loop ([fi fi])
(cond
[(boolean? fi) 0]
[else
(+ 1 (for*/fold ([deepest 0]) ([col (in-vector fi)]
[el (in-vector col)])
(max (loop el) deepest)))])))
(define size (expt 7 depth))
(flomap->bitmap
(flomap-crop
(build-flomap*
1 size size
(λ (x y)
(let loop ([t 0] [l 0] [s size] [fi fi])
(cond
[(eq? fi #t) '#(0.0)]
[(eq? fi #f) '#(1.0)]
[else
; xi and yi are the points within the current level invader
(define xi (quotient (* 7 (- x l)) s))
(define yi (quotient (* 7 (- y t)) s))
(loop (+ t (* yi (/ s 7)))
(+ l (* xi (/ s 7)))
(/ s 7)
(vector-ref (vector-ref fi xi) yi))]))))
(* size 5/7)
(* size 5/7)
1/2
1/2)))
Unfortunately, that first bit is a little bit hacky. Since we’ve split apart the functions that create and render this fractal, we don’t know how large of an image to make. Still, it’s quick enough to calculate. Then, we get into actually making the image. It’s much the same as the code in Fractal Invaders. We recur down, keeping two different sets of coordinates: image coorcinates x, y, t, l, and s and then coordinates within the current level xi and yi. There is a lot of dividing and multiplying by that magic number, but os it goes.
And that’s really it. There’s a call to flomap-crop
, but that’s just to cut off the outermost margin (since it will (1) always be empty and (2) the second level’s margin will still include some spacing). So how does it look?
> (render-invader-fractal (make-invader-fractal 3))

That’s about it. One more trick that I want to do though is to make these reproducable. That we can do some neat tricks with zooming in:
(define-syntax-rule (with-seed seed body* ...)
(parameterize ([current-pseudo-random-generator
(make-pseudo-random-generator)])
(random-seed seed)
body* ...))
(define (invader-fractal i depth)
(with-seed i
(render-invader-fractal (make-invader-fractal depth))))
Because we reset the random seed at the beginning of the calculate and always generate the random numbers from top to bottom, we ned up with some neat effects. The top level with the same seed is always the same shape:
> (for/list ([depth (in-range 1 5)])
(invader-fractal 8675309 depth))
😄
Unfortunately, the lower levels aren’t the same pattern, since we’re generating the images using a depth first search rather than the breadth first search. More specifically, we’re generating the invaders in this order:
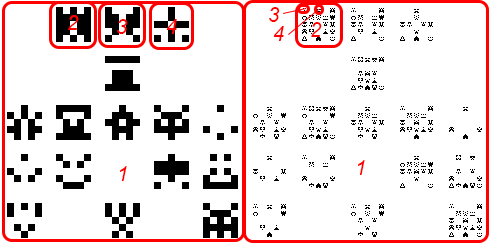
In that case, the ordering is: generate the image for the given level, then the first subimage, then the first subimage of that. Generating the depth first as it were. What we want instead is to generate generate the top level, then all of the next level, then all of the next level, more like this:
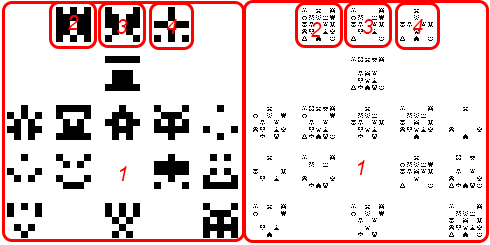
Unfortunately, that doesn’t work out well in our specific code, since we’re working recursively, working with a Stack (computer science) (implicitly via function calls). To do a breadth first search, we would need instead to create a explicit Stack (computer science), which would require some fairly major refactoring.
There’s another option though:
; An invader fractal is nested 5x5 2d vectors, each element is either
; #t/#f - a white/black region
; a recursive 5x5 structure
(define (make-invader-fractal/seeded seed depth)
(define (mod-random-seed! i)
(random-seed (+ 1 (remainder i 2147483646))))
(mod-random-seed! seed)
(let loop ([d depth])
(define invader (flomap-add-margin (procedural-invader (random 32768)) 1))
(for/vector ([x (in-range 7)])
(for/vector ([y (in-range 7)])
(if (> 0.5 (flomap-ref invader 0 x y))
(if (<= d 1)
#t
(begin
(mod-random-seed! (+ (* (- depth d) 49) (* x 7) y seed))
(loop (- d 1))))
#f)))))
(define (invader-fractal seed depth)
(render-invader-fractal (make-invader-fractal/seeded seed depth)))
With the addition of mod-random-seed!, we can set the seed at each level. And we’ve got the amusing notion of non-random random seeds. 😄 But since they’re generated as a function of the current depth and x and y coordinates of the parent image, we’ll always get the same images at each level:
> (for/list ([depth (in-range 1 5)])
(invader-fractal 42 depth))


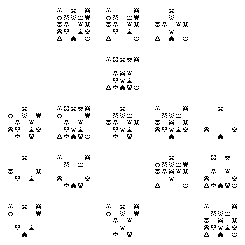

Now that’s what I was looking for. 😄
As always, today’s code is available on GitHub. Check it out: invader-fractals.rkt (Requires procedural-invaders.rkt to run.)
Challenge: Make fractal invaders from invader fractals. Maybe later… 😇
Click to embiggen. ↩︎



