What’s this? Two posts in one day? Well, writing a static blog generator can do that. 😄

Another easily phrased challenge:

We have a simple little problem today: Given an integer n > 2, find the minimum b > 1 for which n base b is a palindrome.

– Minimal Palindromic Base via Programming Praxis

More specifically, consider the number 15:

In this case, 2 is our golden number, since 1111 is a palindrome. But if it wasn’t, 14 is the next case, with 11.

So, what do we need? Well, first we want a generic way to convert bases. We could use different characters up to base 64, but we’ll eventually get beyond that. So instead, we’ll use lists of digits, each of which can be any integer:

; Convert a decimal number n to base b
(define (rebase n b)
  (let loop ([n n] [ls '()])
     (if (= n 0)
        ls
        (loop (quotient n b)
              (cons (remainder n b) ls)))))

> (rebase 15 2)
'(1 1 1 1)

> (rebase 15 5)
'(3 0)

> (rebase 15 10)
'(1 5)

> (rebase 15 14)
'(1 1)

Looks good. Next, we’ll use a macro we’ve often used before: for/first . It’s perfect for our uses, since it will return the first value that is non-#f. In this case, our base:

; Find the minimal base b such that n in base b is a palindrome
(define (minimal-palindromic-base n)
  (for/first ([b (in-naturals 2)]
              #:when (let ([nb (rebase n b)])
                       (equal? nb (reverse nb))))
    b))

Bam. Let’s try a few:

> (minimal-palindromic-base 15)
2

> (minimal-palindromic-base 1234)
22

> (rebase 1234 22)
'(2 12 2)

> (minimal-palindromic-base 8675309)
8675308

Huh. I think 867-5309/Jenny has a secret. 😄

That’s pretty much it for the puzzle as stated, but there are still a few things that we can do. For example, we’ve only seen small examples. What if we want to find the number with the largest minimal palindromic base:

; Find the number n which has the largest palindromic base
(define (maximal-minimal-palindromic-base n-min n-max)
  (for/fold ([b -1] [n #f]) ([i (in-range n-min (+ n-max 1))])
    (define mpb (minimal-palindromic-base i))
    (if (> i b)
        (values mpb i)
        (values b   n))))

I may or may not have just wanted an excuse to use a crazy long function name. 😄

Give it a try:

> (maximal-minimal-palindromic-base 100 200)
7
200

> (rebase 200 7)
'(4 0 4)

Error, maximal-minimal-palindromic-base not found!

Okay, more seriously, what does that even look like? Let’s plot !

(require plot)

; Plot a whole range of minimal palindromic bases
(define (plot-minimal-palindromic-bases n-min n-max)
  (plot (lines (for/list ([i (in-range n-min (+ n-max 1))])
                 (vector i (minimal-palindromic-base i)))
               #:color 6
               #:label "minimal palindromic base")))

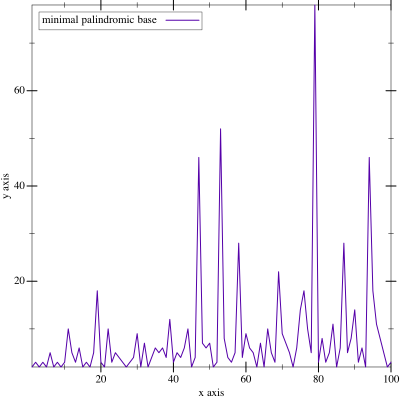
Basically, we’re going to draw a chart relating each number to it’s minimal palindromic base.

(plot-minimal-palindromic-bases 1 100)

(plot-minimal-palindromic-bases 1 1000)

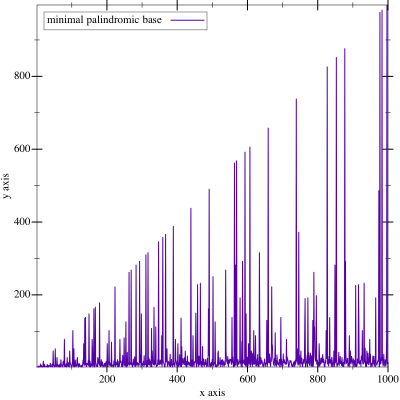
Looks like like there’s basically two behaviors. A background noise of really low bases (binary or trinary is often palindromic just because there aren’t many digits) and a few spikes growing ever larger. Neat.

And that’s it. Code: minimal-palindromic-base.rkt