Hey, remember that post a few days ago about the Cracker Barrel peg game? Right at the end, I mentioned that there would be a part two, all about how to bend the puzzle at least a bit to your advantage. Basically, rather than finding the first solution to the peg game, we’re going to find all of them. From there, we can determine which moves are easier to win from, which are harder, and which are downright impossible. Let’s do it!
Okay, first things first. Remember how we represented the puzzles as either a 15 element vector or 15 bit integer? Well that gives us a pretty solid upper bound on how many possible ways that the puzzle can end up being arrange. Specifically, 2^{15 = 32768} total states. For a computer… that’s actually not that big of a number. First, let’s see how many of those we can actually reach.
; Count how many total states are reachable from any initial state
; By default, start with one copy of each peg missing
(define (reachable [queue (for/list ([i (in-range 15)])
(invert (make-puzzle (expt 2 i))))])
(let loop ([reached (hash)] [queue queue])
(cond
; Queue is empty, done
[(null? queue)
reached]
; Already checked this state, check the rest
[(hash-ref reached (index (first queue)) #f)
(loop reached (rest queue))]
; New state, add it to the hash and all next states to the queue
[else
(loop (hash-set reached (index (first queue)) #t)
(append (rest queue) (next (first queue))))])))
Hopefully straight forward algorithm, basically we start with an (empty) index of which nodes we’ve visited–a hash in our case. Start with each of the fifteen opening moves in a queue. Then, keep taking one nodes off the queue. For new nodes, add that to the list of visited nodes and all its neighbors to the queue. A breadth-first search. Give it a run:
> (hash-count (reachable))
13935
So only 42.5%. Huh. A few examples of states that can’t be reached:
> (define r (reachable))
> (for/list ([i (in-range 5)])
(let loop ()
(define p (make-puzzle (random (expt 2 15))))
(if (hash-ref r (index p) #f)
(render p)
(loop))))
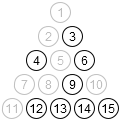
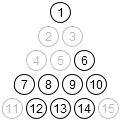
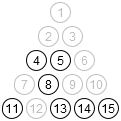
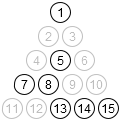
But that doesn’t necessary tell us which starting positions are easier. For that, we need something more like this:
> (require plot)
> (plot (discrete-histogram
(for/list ([i (in-range 15)])
(vector (+ i 1)
(hash-count (reachable (list (invert (make-puzzle (expt 2 i))))))))))
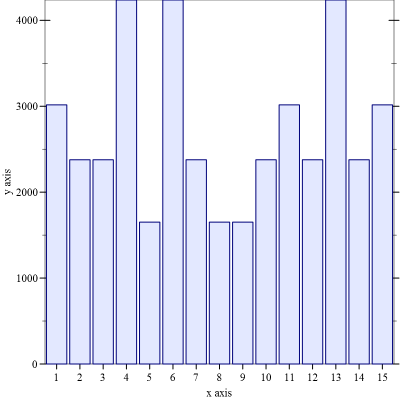
Interesting. So there are three states that reach the most (4, 6, and 13), three on the next tier (1, 11, and 15), 6 on the next, and 3 that reach the least (5, 8, and 9). If you think about it, that makes a lot of sense. For each position, there are two other identical positions–rotations:
; Rotate a puzzle clockwise
(define (rotate p)
(puzzle (for/vector ([i (in-list '(11 12 7 13 8 4 14 9 5 2 15 10 6 3 1))])
(vector-ref (puzzle-data p) (- i 1)))))
> (define random-puzzle (make-puzzle (random (expt 2 15))))
> (map render (list random-puzzle
(rotate random-puzzle)
(rotate (rotate random-puzzle))))

Further than that, there are also reflections:
; Reflect a puzzle left to right
(define (reflect p)
(puzzle (for/vector ([i (in-list '(1 3 2 6 5 4 10 9 8 7 15 14 13 12 11))])
(vector-ref (puzzle-data p) (- i 1)))))
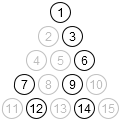
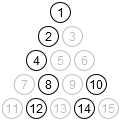
This is what I meant last time, when I said that there were only four initial states (1, 2, 4, and 5). All of the rest are reflections and/or rotations of one of those 4.
Finally, if you combine these two functions, it should be possible to get a real idea of how many truly unique states there are. Since each puzzle has a numeric form and each puzzle has up to six unique states (three rotations, each with two reflections), we can consistently find the one of those six with the lowest value. Something like this:
; Minimize a puzzle by finding the reflection/rotation with the minimal vector
(define (minify p)
(define r1 (rotate p))
(define r2 (rotate r1))
(first (sort (list p r1 r2 (reflect p) (reflect r1) (reflect r2))
(λ (p1 p2)
(< (index p1) (index p2))))))
> (map index (list random-puzzle
(reflect random-puzzle)
(rotate random-puzzle)
(reflect (rotate random-puzzle))
(rotate (rotate random-puzzle))
(reflect (rotate (rotate random-puzzle)))))
'(26794 21322 10025 7474 12412 12679)
> (index (minify random-puzzle))
7474
> (render (minify random-puzzle))
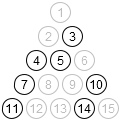
So how many states do we get if we take only the minimum form? Both overall and reachable?
> (set-count
(for/set ([i (in-range (expt 2 15))])
(index (minify (make-puzzle i)))))
5728
; Modification of reachable states, only minified
; By default, start with one copy of each peg missing
(define (reachable-min [queue (for/list ([i (in-range 15)])
(invert (make-puzzle (expt 2 i))))])
(let loop ([reached (hash)] [queue queue])
(cond
; Queue is empty, done
[(null? queue)
reached]
; Already checked this state, check the rest
[else
(define p (minify (first queue)))
(define i (index p))
(cond
[(hash-ref reached i #f)
(loop reached (rest queue))]
[else
(loop (hash-set reached i #t)
(append (rest queue) (next p)))])])))
> (hash-count (reachable-min))
2383
Still about the same (technically slightly lower, it’s only 41.6%). That’s a good sign. We’re all of the way down to 2,383 states from the original potential 32,768. A lot more manageable.
Next, let’s shift to moves rather than states. Given two states, they are connected with a move if you could make a single jump to get from one to the other. So now rather than a set, we have a graph. Something like this:
; Find a map of all possible moves from a given puzzle
(define (all-moves p)
(define moves (make-hash))
(let loop ([p p])
(let ([p (minify p)])
(define i (index (minify p)))
(when (not (hash-has-key? moves i))
(define next-ps (next p))
(hash-set! moves i (list->set (map index (map minify next-ps))))
(map loop next-ps))))
moves)
From there, we can recursively build up a count for each state how many times we win (end up with only a single peg) and how many times we lose.
; Count the number of winning and losing states from a given puzzle
(define (score p)
(define moves (all-moves p))
(define-values (wins losses)
(let loop ([i (index (minify p))])
(define nxt (hash-ref moves i (set)))
(cond
[(set-empty? nxt)
(if (= 1 (count (make-puzzle i)))
(values 1 0)
(values 0 1))]
[else
(for/fold ([wins 0] [losses 0]) ([n (in-set nxt)])
(define-values (r-wins r-losses) (loop n))
(values (+ wins r-wins)
(+ losses r-losses)))])))
(* 1.0 (/ wins (+ wins losses))))
That way we can tell how ‘hard’ each puzzle is, assuming that you always rotate/reflect to avoid potential duplicate state:
> (for/list ([i (in-list '(1 2 3 5))])
(list i (score (invert (make-puzzle i)))))
'((1 0.05239514926876435)
(2 0.05138285262741999)
(3 0.08392304995059131)
(5 0.08392304995059131))
So there you have it. If you’re playing optimally, it’s slightly easier to do so starting with a corner or the second. The center or center of each edge are slightly harder.
And that’s all we have for today. Originally, I meant to use the graph library I’ve used a number of times before to visualize the solution space (there’s a function that will do that on GitHub), but the graphs honestly aren’t that helpful. There nodes are too nested and there are just too many to helpfully visualize. So it goes. Still, I think we found a few interesting things.
As always, the code is available on GitHub: pegs.rkt