About two weeks ago, I came across a post via /r/programming: Quadtree Art(src). In a sentence, the goal is to recursively divide an image into a quadtree, at each step expanding the current node with the largest internal variance.
More specifically, the algorithm is as follows:
- Given an image \mathbb{I}
- Split the image into four subimages, \mathbb{I}_1 - \mathbb{I}_4
- For each current node \mathbb{I}_i , calculate the median color \mathbb{A}_i and error \mathbb{E}_i = \sum \begin{vmatrix} \mathbb{I}(x,y) - \mathbb{A}_i \end{vmatrix}
- Find the subimage with the largest error, split it into four further subimages
- Repeat from step 3
And if you can do all of that, you can get some pretty neat images:

But how do we turn that into code?
Quadtrees
Well, first we have to take a step back. We need some way of representing a quadtree. Perhaps a structure something like this:
(struct quadtree (top-left top-right bottom-left bottom-right) #:transparent)
Then, each node will either be a further quadtree or a leaf (any sort of value). If we wanted to have a quadtree of numbers:
1 | 2 3
| 4 5
----+-----
6 | 7 8
| 9 0
We could do so like this:
> (define qt (quadtree 1 (quadtree 2 3 4 5) 6 (quadtree 7 8 9 0)))
> qt
(quadtree 1 (quadtree 2 3 4 5) 6 (quadtree 7 8 9 0))
Recursive data structures at their finest 😄.
The next thing we want is a trio of helper functions: quadtree-map, quadtree-reduce, and quadtree-ref. In order, these will apply a function to each node in a quadtree, collapse a quadtree by replacing the structure of the tree with a function (I’ll show an example later), or find a specific point within the quad tree.
First, map:
; Map a function over the nodes in a quadtree
(define (quadtree-map f qt)
(cond
[(quadtree? qt)
(quadtree
(quadtree-map f (quadtree-top-left qt))
(quadtree-map f (quadtree-top-right qt))
(quadtree-map f (quadtree-bottom-left qt))
(quadtree-map f (quadtree-bottom-right qt)))]
[else (f qt)]))
Easy enough. Saw we want the square of each value in the previous quadtree:
> (quadtree-map sqr qt)
(quadtree 1 (quadtree 4 9 16 25) 36 (quadtree 49 64 81 0))
Next, quadtree-reduce. To think about this one, look at the structure of a quadtree in the above example. Each quadtree call looks an awful lot like a function call. That’s really all that a reduce is, is swapping out the call for another function. Something like this:
; Reduce all nodes in a quadtree
(define (quadtree-reduce f qt)
(cond
[(quadtree? qt)
(f (quadtree-reduce f (quadtree-top-left qt))
(quadtree-reduce f (quadtree-top-right qt))
(quadtree-reduce f (quadtree-bottom-left qt))
(quadtree-reduce f (quadtree-bottom-right qt)))]
[else qt]))
So to add all of the nodes together:
> (quadtree-reduce + qt)
45
> qt
(quadtree 1 (quadtree 2 3 4 5) 6 (quadtree 7 8 9 0))
> (+ 1 (+ 2 3 4 5) 6 (+ 7 8 9 0))
45
Or always take the top right node:
> (quadtree-reduce (λ (tl tr bl br) tr) qt)
3
And finally, reference a specific point. This is the first time that we’re dealing with quadtrees as a representation of space. Think of a space, saw 16 meters square. If you take the top right, you have from 0-8 on the y and 8-16 on the x. Take the top left of that and you have 0-4 on the y and 8-12 on the x.
In code:
(struct region (top left width height) #:transparent)
; Recur to a given point within a quadtree
(define (quadtree-ref qt width height x y #:return-region [return-region? #f])
(let loop ([qt qt] [r (region 0 0 width height)])
(cond
[(quadtree? qt)
(match-define (region top left width height) r)
(define x-mid (+ left (quotient width 2)))
(define y-mid (+ top (quotient height 2)))
(match (list (if (< y y-mid) 'top 'bottom)
(if (< x x-mid) 'left 'right))
['(top left) (loop (quadtree-top-left qt) (region top left (quotient width 2) (quotient height 2)))]
['(bottom left) (loop (quadtree-bottom-left qt) (region y-mid left (quotient width 2) (quotient height 2)))]
['(top right) (loop (quadtree-top-right qt) (region top x-mid (quotient width 2) (quotient height 2)))]
['(bottom right) (loop (quadtree-bottom-right qt) (region y-mid x-mid (quotient width 2) (quotient height 2)))])]
[return-region? r]
[else qt])))
It’s a bit more complicated, but should be straight forward enough to read. Perhaps the most interesting part is the use of match-define
. Given a struct (such as a region), it can automatically destructure it. Much easier than a whole series of defines.
Whew.
Rendering quadtrees
Next, we need to actually turn one of these quadtrees back to an image. It turns out though, that that part is really easy. If we have a quadtree where each node is either recursive or a color (represented as a 4 vector of ARGB), you can render it as such:
; Render a tree where each node is either a quadtree or a vector (color)
(define (render-quadtree qt width height)
(flomap->bitmap
(build-flomap*
4 width height
(λ (x y) (quadtree-ref qt width height x y)))))
As an example:
> (render-quadtree
(quadtree '#(1 1 0 0)
(quadtree '#(1 0 1 0) '#(1 0 0 1) '#(1 0 1 1) '#(1 1 0 1))
'#(1 1 1 0)
(quadtree '#(1 1 1 1) '#(1 0 0 0) '#(1 0 0 0) '#(1 1 1 1)))
100 100)

Loading images as quadtrees
Okay, next step. Loading an image. What we want for an image is the original (so we can calculate the error) and a quadtree storing both average colors for each region (which will be rendered) and the error (so we do not have to recalculate them). Something like this:
(struct qtnode (region color error) #:transparent)
(struct qtimage (flomap nodes))
(qtimage is not #:transparent since the flomap would display every single value… That takes a while to print out.)
That being said, when we first load an image, we’re only going to have a single node representing the entire image. Still, we need an average and an error. So let’s write that function first. Using the median
function from math/statistics
, we can find a good representation (another option would be the average). After that, we sum the difference along all channels (note: make sure to use for*/sum here, rather than for/sum…)
; Calculate the average color within a region
(define (region-node fm r)
(match-define (region top left width height) r)
(define med
(for/vector ([k (in-range 4)])
(with-handlers ([exn? (λ _ (flomap-ref fm k left top))])
(median < (for/list ([x (in-range left (+ left width))]
[y (in-range top (+ top height))])
(flomap-ref fm k x y))))))
(define err
(for*/sum ([k (in-range 4)]
[x (in-range left (+ left width))]
[y (in-range top (+ top height))])
(abs (- (flomap-ref fm k x y) (vector-ref med k)))))
(qtnode r med err))
Then you can load an image:
; Load an image in preparation for quadtree splitting
(define (load-image path)
(define fm (bitmap->flomap (read-bitmap path)))
(define-values (width height) (flomap-size fm))
(define r (region 0 0 width height))
(define node (region-node fm r))
(qtimage fm node))
If we want to turn right around and render this image back out, we can do so by pulling out the color part of the quadtree nodes:
; Render an image
(define (render-image img)
(define-values (width height) (flomap-size (qtimage-flomap img)))
(render-quadtree (quadtree-map qtnode-color (qtimage-nodes img)) width height))
Given pipes.jpg:

> (render-image (load-image "pipes.jpg"))

Not much to look at yet. We need to start splitting…
Splitting quadtree images
A lot of the hard work has already been done. What’s left is two parts:
- Find the region with the largest error
- Replace that node with four subnodes, calculating the median color and error for each
Translated to code:
; Given an image, split the region with the highest error
(define (split-image img)
; Find the maximum error
(define max-error-node
(quadtree-reduce
(λ ns (car (sort ns (λ (na nb) (> (qtnode-error na) (qtnode-error nb))))))
(qtimage-nodes img)))
; Replace nodes with that error with their child nodes, calculating those errors
(define fm (qtimage-flomap img))
(qtimage
fm
(quadtree-map
(λ (node)
(cond
[(eq? node max-error-node)
(match-define (region t l w h) (qtnode-region node))
(define w/2 (quotient w 2))
(define h/2 (quotient h 2))
(quadtree
(let ([r (region t l w/2 h/2)]) (region-node fm r))
(let ([r (region t (+ l w/2) w/2 h/2)]) (region-node fm r))
(let ([r (region (+ t h/2) l w/2 h/2)]) (region-node fm r))
(let ([r (region (+ t h/2) (+ l w/2) w/2 h/2)]) (region-node fm r)))]
[else node]))
(qtimage-nodes img))))
The splitting code is a little ugly and could probably be factored out entirely into a region module all its own. So it goes. What’s nice though is that we already have the region-node function, which will give us the color and error for a subnode.
Trying a few splits:
> (render-image (split-image (load-image "pipes.jpg")))
> (render-image
(for/fold ([img (load-image "pipes.jpg")]) ([i (in-range 5)])
(split-image img)))

> (render-image
(for/fold ([img (load-image "pipes.jpg")]) ([i (in-range 1000)])
(split-image img)))

That’s really starting to look good… But what if we want to watch the compression live?
Rendering compression
This is one of the things I really like about Racket. It really is “batteries included”. In this case, we have a pre-built framework for updating and rendering images: big-bang
from 2htdp/universe
(among others). All we have to do is pass it an updating and drawing function (render? will allow us to save a GIF):
; Progressively compress an image
(define (compress img)
(define-values (width height) (flomap-size (qtimage-flomap img)))
(define base-scene (empty-scene width height))
(big-bang img
[on-tick split-image]
[to-draw (λ (img) (place-image (render-image img) (/ width 2) (/ height 2) base-scene))]
[record? #t]))
Bam:
> (compress (load-image "pipes.jpg"))
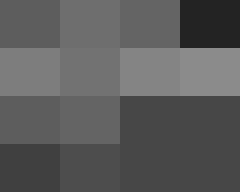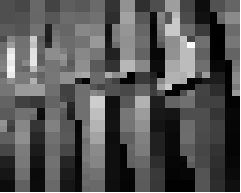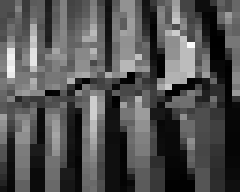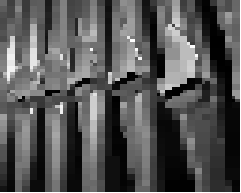
> (compress (load-image "bigen.jpg"))
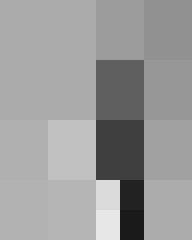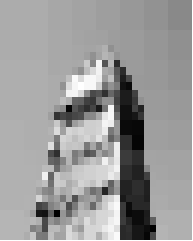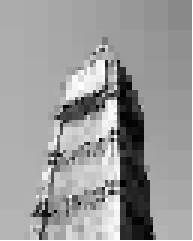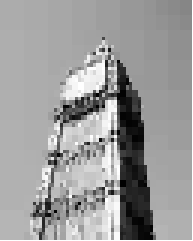
> (compress (load-image "chess.jpg"))

> (compress (load-image "flower.jpg"))

And there you have it. I really like digging into alternative ways of representing data, particularly images. If you have any questions/comments, feel free to drop me a line below. Otherwise, the code is on GitHub as always: quadtree-compression.rkt.