Another day, another challenge from /r/dailyprogrammer. It’s almost two weeks old now, but I’ve just now had a chance to get around it.
Your company has built its own telephone network. This allows all your remote locations to talk to each other. It is your job to implement the program to establish calls between locations.
Problem description
Basically, this is an exercise in graph theory. Given a weighted graph (in this case representing locations in our call network and the maximum bandwidth between locations), route a series of calls between the nodes. There’s an aspect of optimization to it as well, although if you cannot see the future, there’s only so much you can do to be able to guess what future calls you’ll have to route.
As stated in the problem, our input will be given by a list of source, destination, weight triples. Something like this:
A B 2
A C 2
B C 2
B D 2
C E 1
D E 2
D G 1
E F 2
F G 2
Unusually for an /r/dailyprogrammer challenge, there isn’t an indication for how many records we have to read. Instead, there will be a blank line at the end of the section. Still, that’s easy enough to deal with. Something like this:
; Read a phone network as a weighted undirect graph, form {from} {to} {weight}
(define (read-network [in (current-input-port)])
(define g (weighted-graph/directed '()))
(for ([line (in-lines in)]
#:break (equal? line ""))
(match-define (list from to weight) (string-split line))
(add-edge! g from to (string->number weight))
(add-edge! g to from (string->number weight)))
g)
(We’re using stchang’s [1][2].)
After that, we’ll have a series of calls to route:
A G
A G
C E
G D
D E
A B
A D
In this case, each call will be a pair of nodes, the source and the destination (although routes are not directional). Since we’re reading to the end of the file and only reading two parts, the code is much cleaner.
; Read a sequential list of calls formatted as {from} {to}
(define (read-calls [in (current-input-port)])
(for/list ([line (in-lines in)])
(string-split line)))
So we’ve gotten the problem read in, now all that’s left is solving it. 😄
Routing calls
First things first, what are we going to return? Eventually, I need to have a list of paths (one for each call) or a failure if we couldn’t route a particular call. In addition, I want to keep the current network at each step, to help with debugging. So perhaps something like this:
; Each step of a solution will have
; - the current graph (before routing)
; - the call being made
; - the found route (or #f)
(struct step (graph call route) #:transparent)
Other than that, the algorithm is straight forward. For each call, find a route. If we find a route, reduce the bandwidth on each node. If not, report failed and leave the network alone.
Technically, finding the paths is interesting in and of itself. There are a number of algorithms, depending on which route you’re looking for. One of particular interest is Dijkstra’s algorithm, which already has an implementation of sorts in the library I’m using. One thing that it doesn’t do; however, is route from one node to another, it actually does far more, routing from one node to all others (a natural result of running Dijkstra’s algorithm anyways). So we need a function that will extract a single path from that result:
; Specialization of the graph library to find a single path using dijkstra's
(define (dijkstra-path graph from to)
(define-values (_ preds)
(dijkstra graph from))
(let loop ([to to] [path '()])
(cond
[(equal? from to)
(cons to path)]
[(hash-ref preds to #f)
=> (λ (next)
(loop next (cons to path)))]
[else
#f])))
Using the => form of cond, we can return the path if there is one, or immediately short circuit with no path if we ever fail. Additionally, using an accumulator (path), means that the list is naturally in the order we want, where it would have been reversed in the more ’natural’ recursive form.
That’s basically everything we need. Given functions to read in the data and a path finder for each step, we can solve the entire call set:
; Given a phone network and sequence of calls, place as many as possible
(define (solve [in (current-input-port)])
(define network (read-network in))
(define calls (read-calls in))
; Try to route each call in turn
; Take the shortest path possible using dijkstra's algorithm for routing
(for/list ([call (in-list calls)])
(match-define (list from to) call)
(cond
; We can find a path; write it and update the network
[(dijkstra-path network from to)
=> (λ (path)
(begin0
(step (graph-copy network) call path)
(let loop ([path path])
(match path
; As long as there are at least two nodes:
; - Calculate the new edge weight
; - Remove the current edge (no way to directly update)
; - If new weight is not zero, add the new edges
[(list-rest from to rest)
(define weight (- (edge-weight network from to) 1))
(remove-edge! network from to)
(remove-edge! network to from)
(when (> weight 0)
(add-edge! network from to weight)
(add-edge! network to from weight))
(loop rest)]
[any (void)]))))]
; No path; print failure and leave the network
[else
(step (graph-copy network) call #f)])))
Honestly, adding and removing the nodes is the largest part of the code. Perhaps I should add in an edit-weight! function. Anyways, this gives us a simple enough way to solve the problems given:
> (with-input-from-string "A B 1
B C 2
C D 2
D E 2
E F 2
F G 2
G A 2
E H 1
H D 1
A C
A D
A D
F D
B D
B D
B E
C F" solve)
(list
(step #<weighted-graph> '("A" "C") '("A" "B" "C"))
(step #<weighted-graph> '("A" "D") '("A" "G" "F" "E" "D"))
(step #<weighted-graph> '("A" "D") '("A" "G" "F" "E" "D"))
(step #<weighted-graph> '("F" "D") #f)
(step #<weighted-graph> '("B" "D") '("B" "C" "D"))
(step #<weighted-graph> '("B" "D") '("B" "C" "D"))
(step #<weighted-graph> '("B" "E") #f)
(step #<weighted-graph> '("C" "F") #f))
So for this case, we could only route 5 of the 8 calls. Oops. It turns out there’s a solution that routes 6 of them, but only if you can see the future and purposely don’t route one of the early further apart calls.
Well, that’s all well and good, but how about some visualization?
Visualizing output
My goal is going to be to write out a ‘solution directory’. First, we need a summary file (actually writing out the solution the problem asked for):
; Write a solution to a directory
(define (write-solution steps output-directory)
; Make sure the output directory exists (files will be overwritten)
(when (not (directory-exists? output-directory))
(make-directory output-directory))
; First generate a summary file
(with-output-to-file (build-path output-directory "summary.txt")
(thunk
(for ([i (in-naturals 1)]
[each (in-list steps)])
(match-define (step network call path) each)
(match-define (list from to) call)
(printf "~a -> ~a ... ~a\n"
from
to
(or path "failed")))))
...)
Straight foward enough. The only interesting piece is writing either the path or “failed”, which we can get away with because or short circuits. Easy enough.
Next, display the networks:
...
; Generate a graph for each step
(for ([i (in-naturals 1)]
[each (in-list steps)])
(match-define (step network call path) each)
; Generate a coloring with distinct colors for path
(define colors
(for/hash ([node (in-vertices network)])
(values node (cond
[(equal? node (first path)) 1]
[(equal? node (last path)) 2]
[(member node path) 3]
[else 0]))))
; Paramaterize each step filename so we can make dots and images
(define (filename ext)
(format "~a.~a"
(~a i #:min-width 2 #:align 'right #:pad-string "0")
ext))
; Write the dot file
(with-output-to-file (build-path output-directory (filename "dot"))
#:exists 'replace
(thunk
(display (graphviz network #:colors colors))))
; Use the dot file to generate an image
(system (format "neato -Tpng ~a > ~a"
(build-path output-directory (filename "dot"))
(build-path output-directory (filename "png"))))))
It’s a bit complicated looking, but really there are four parts. First, we generate a coloring. A little while ago I made the function that would successfully display a coloring, so for that we need to create a hash of vertex labels to integers. In this case, we’ll have distinct colors for the source (green), path (purple), destination (cyan), and unrelated nodes (red). Something like this:
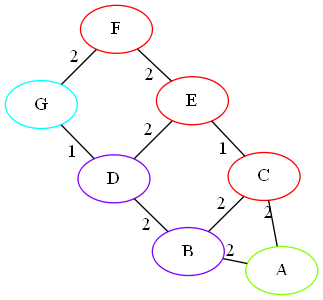
The next part generates a filename generating function (so we can parameterize over the extension). Straight forward, we just want to make sure we have two digits so they’ll sort correctly, thus the use of ~a (I wish there were a shorter way to do this).
After that, write out the file generated by the graphviz function, then call neato on my local system to generate the image. From that, we get a nice series of images:
summary.txt:
A -> G ... (A B D G)
A -> G ... (A C E F G)
C -> E ... (C E)
G -> D ... (G F E D)
D -> E ... (D E)
A -> B ... (A B)
A -> D ... (A C B D)
[gallery link=“file” columns=“3” orderby=“title”]
Yay graphs!
And that’s it for today. If you want to see the entire code all in one place, you can do so on GitHub as always: phone-network.rkt