Pretty pretty picture time1:
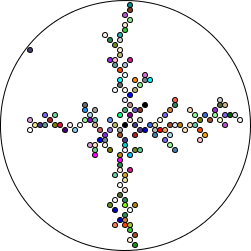
The basic idea here is that of a Brownian Tree:
A Brownian tree is built with these steps: first, a “seed” is placed somewhere on the screen. Then, a particle is placed in a random position of the screen, and moved randomly until it bumps against the seed. The particle is left there, and another particle is placed in a random position and moved until it bumps against the seed or any previous particle, and so on.
– Wikipedia
In this case, we’re going to put the seed point in the center and drop points in from the outside. There are a number of other parameters we can tweak, but we’ll get to each of those in turn.
First, we need to come up with a basic structure for the code. Luckily, the big-bang
function will do exactly what we want. All we have to do it write something for the on-tick and on-draw clauses.
Okay, next step. What sort of data structure are we going to use?
Well, we need to know how big the world is. And we need to have a bunch of dots moving constantly inwards, so how about something like this:
(struct point (x y) #:transparent)
(struct world (radius points drip) #:transparent)
I went ahead and separated out the point that is currently falling inwards as the drip, although we could also have had that as the first of the list in points. Either works.
Okay, so next we want a function that takes in one of these world structures and returns the next step in the simulation. In this case, the drip should either move inwards or freeze in place if it meets another nearby point. Perhaps something like this:
; Either randomly move the drip or create a new one
(define (update w)
; Always try to move the drip first
(define new-drip
(point (+ (point-x (world-drip w)) (random 3) -1)
(+ (point-y (world-drip w)) (random 3) -1)))
(cond
; If it's adjacent to any current point, freeze it and generate a new drip
[(ormap (λ (pt) (<= (δ new-drip pt) (current-spacing)))
(world-points w))
(world (world-radius w)
(cons new-drip (world-points w))
(random-point (world-radius w)))]
; Otherwise, just use the new drip
[else
(world (world-radius w)
(world-points w)
new-drip)]))
As the comments say, we’ll start by moving the point. Then, we can check if the new-drip is adjacent to any neighboring point by calculating the distance to each with δ:
; Distance formula
(define (δ pt1 pt2)
(sqrt (+ (sqr (- (point-x pt1) (point-x pt2)))
(sqr (- (point-y pt1) (point-y pt2))))))
Furthermore, because we’re using ormap, as soon as we have any matching point, the check will short circuit. If we wanted to write it in a potentially more ‘Rackety’ style, we could instead have written the condition with for/first
:
(for/first ([pt (in-list (world-points w))]
#:when (<= (δ new-drip pt) (current-spacing)))
#t)
The last bit is the random-point function. Since we’re dealing with a circle, it will be easiest to generate the points in polar coordinates and then converting them to Cartesian coordinates:
; Generate a new random point on the border of a given circle
(define (random-point r)
(define θ (* 2 pi (random)))
(point (inexact->exact (truncate (* r (cos θ))))
(inexact->exact (truncate (* r (sin θ))))))
If you wanted to generate points within the circle as well, rather than just on the edge, you could randomly generate (define r^ (* (random) r)). I think generating them on the borders works better though.
Well, that was straight forward enough> Hopefully the drawing function will be as quick?
For this, we’re going to take advantage of the circle
and overlay/offset
functions, both from 2htdp/image
. The former will create a circular image (either for the background or for the points themselves) and the latter will draw the latter on the former (nicely centering them for a convenient axis system).
Something like this:
; Draw the current points in an image
(define (draw w)
(for/fold ([img (circle (world-radius w) "outline" "black")])
([pt (in-list (cons (world-drip w)
(world-points w)))])
(overlay/offset (outlined-circle 0.5 "black")
(point-x pt)
(point-y pt)
img)))
I really like the for/fold
macro. The first block starts with the loop state (the background circle). The second controls the loop (the drip and then each point in turn). The third/body draws the point with the next loop acting as the img the next time around.
Now, the beauty of this structure becomes apparent. With the big-bang
function from 2htpd/universe
, all we have to do is create an initial world and the update/draw functions:
(define (brownian-tree radius)
(big-bang (world radius '() (point 0 0))
(on-tick update)
(on-draw draw)))
Let’s give it a try:
> (brownian-tree 25)

Yeah, that’s tiny. Perhaps as the first tweak, we should introduce a scaling parameter to the world. The nice thing about the update/draw split is that we can keep the simulation unscaled and only scale in draw:
(struct world (radius scale points drip) #:transparent)
; Draw the current points in an image
(define (draw w)
(for/fold ([img (circle (* (world-scale w) (world-radius w)) "outline" "black")])
([pt (in-list (cons (world-drip w)
(world-points w)))])
(overlay/offset (outlined-circle (/ (world-scale w) 2) "black")
(* (world-scale w) (point-x pt))
(* (world-scale w) (point-y pt))
img)))
(define (brownian-tree radius #:scale [scale 1.0])
(big-bang (world radius scale '() (point 0 0))
(on-tick update)
(on-draw draw)))
Optional keyword parameters, just because…
With that, we can make some much more reasonably sized images:
> (brownian-tree 25 #:scale 5.0)
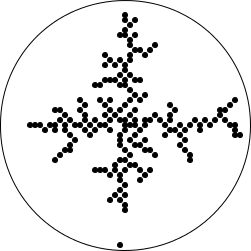
What’s the next thing we could tweak? How about a bit more color?
(struct point (x y c) #:transparent)
; Generate a new random point on the border of a given circle
(define (random-point r)
(define θ (* 2 pi (random)))
(point (inexact->exact (truncate (* r (cos θ))))
(inexact->exact (truncate (* r (sin θ))))
(vector-ref colors (random (vector-length colors)))))
; Draw the current points in an image
(define (draw w)
(for/fold ([img (circle (* (world-scale w) (world-radius w)) "outline" "black")])
([pt (in-list (cons (world-drip w)
(world-points w)))])
(overlay/offset (outlined-circle (/ (world-scale w) 2) (point-c pt))
(* (world-scale w) (point-x pt))
(* (world-scale w) (point-y pt))
img)))
(define (brownian-tree radius #:scale [scale 1.0])
(define origin (point 0 0 "black"))
(big-bang (world radius scale (list origin) (random-point radius))
(on-tick update)
(on-draw draw)))
That’s actually enough to generate the image from the header:
> (brownian-tree 25 #:scale 5.0)

There are two things that you should have noticed though–although one isn’t particularly obvious unless you’re following along:
- The grid structure tends to align on the vertical and horizontal axes
- It takes forever for the points to fall inwards and join the tree
How can we deal with that?
Well for the first, think back to the update function we wrote. All we really used was a grid update that added ±1 to each point and a distance function δ. There’s nothing in particular that would stop us from moving with real coordinates instead. To make the transition easier, let’s factor out this ‘wiggle’ function into two different options:
(define current-wiggle-real? (make-parameter #f))
(define current-inward-bias (make-parameter 0.5))
; Wiggle a point closer to the origin, sticking to the unit grid
(define (wiggle:grid pt)
(let ([max-d (δ origin pt)])
(let loop ()
(define xδ? (zero? (random 2)))
(define new-pt
(point (if xδ? (+ (point-x pt) (random 3) -1) (point-x pt))
(if xδ? (point-y pt) (+ (point-y pt) (random 3) -1))
(point-c pt)))
(if (or (<= (δ origin new-pt) max-d) (< (current-inward-bias) (random)))
new-pt
(loop)))))
; Wiggle a point closer to the origin, returning any new point within the unit circle
(define (wiggle:real pt)
(let ([max-d (δ origin pt)])
(let loop ()
(define θ (* 2 pi (random)))
(define new-pt
(point (+ (point-x pt) (cos θ))
(+ (point-y pt) (sin θ))
(point-c pt)))
(if (or (<= (δ origin new-pt) max-d) (< (current-inward-bias) (random)))
new-pt
(loop)))))
; Either randomly move the drip or create a new one
(define (update w)
; Always try to move the drip first
(define new-drip
((if (current-wiggle-real?) wiggle:real wiggle:grid)
(world-drip w)))
...)
(define (brownian-tree radius
#:scale [scale 1.0]
#:spacing [spacing 1]
#:real-mode [real-mode? #f])
(parameterize ([current-wiggle-real? real-mode?]
[current-spacing spacing])
(define origin (point 0 0 "black"))
(big-bang (world radius scale (list origin) (random-point radius))
(on-tick update)
(on-draw draw))))
While we’re at it, I made another tweak for the second issue above. Did you notice? current-inward-bias? Basically, a random percent of the number, we might move outwards, but otherwise we’re guaranteed (via checking the δ to the origin) to move inwards. This should speed up the simulation–while at the same time adding enough parameters to get all sorts of interesting variants:
| bias | 1.0 | 0.5 | 0.25 |
| grid | 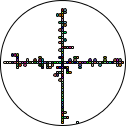 | 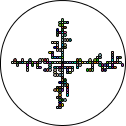 | 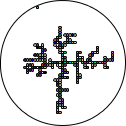 |
| real | 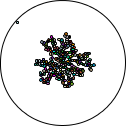 | 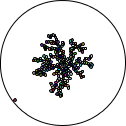 | 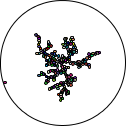 |