Here’s another one from /r/dailyprogrammer:
… Your goal is to color a map of these regions with two requirements: 1) make sure that each adjacent department do not share a color, so you can clearly distinguish each department, and 2) minimize these numbers of colors.
Essentially, graph coloring.
Of course we’ll go ahead and use the yesterday’s post. The input format is a little different this time, where each line contains a node then all of the neighbors, but that shouldn’t be an issue. We just need a slightly different read-graph function:
; Given a string or input port, read a graph
; First line is number of following lines
; The rest of the lines have a node id than one or more ids of that node's neighbors
(define (read-graph [str/in (current-input-port)])
(define in (if (string? str/in) (open-input-string str/in) str/in))
(define node-count (read in))
(define g (unweighted-graph/undirected '()))
(for* ([i (in-range node-count)]
[line (in-lines in)])
(define nums (map string->number (string-split line)))
(when (> (length nums) 1)
(for ([n (in-list (rest nums))])
(add-edge! g (first nums) n))))
g)
After that, we have to figure out what strategy we want to use to color the graph. It turns out that even determining how many colors the best coloring would need is hard1. That means that a perfect solution is going to be slow, especially as the problem gets bigger. So how about instead we start out with a very basic greedy algorithm and go from there.
Idea the first: Iterate through the nodes of the graph, coloring each one in turn. Use the first available color that hasn’t already been assigned.
; Assign a color given a graph, color hash, and node
(define (assign-first-color! g cs n)
(for/first ([i (in-naturals)]
#:unless
(member i (map (λ (n) (hash-ref cs n #f))
(neighbors g n))))
(hash-set! cs n i)))
; Basic greedy coloring: color each node in turn with the first available color
(define (greedy-coloring g [node-order (in-vertices g)])
(define colors (make-hash))
; For each node, try each color
; for/first will bail as soon as it is execute once
(for ([n (in-list node-order)])
(assign-first-color! g colors n))
colors)
There’s a bit of voodoo magic in the first method, but basically I’m using for/first to short circuit the loop. Previously, I’ve done much the same thing with let/ec, but this feels more ‘Rackety’. Essentially, we run through the colors (represented as numbers) until we find one that isn’t a member of the list of all neighboring colors. As soon as we see that, we assign the color and bail out of the loop.
The second function takes the graph and a node ordering (which defaults to whatever is being internally stored in the graph) and repeatedly uses the assignment function to color nodes. To test it out, let’s use that same Butterfly graph as yesterday:
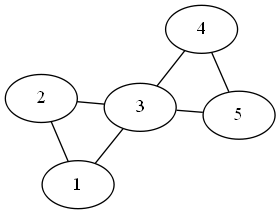
Assigning the nodes left to right then top to bottom, we have:
> (define butterfly (read-graph "
5
1 2 3
2 1 3
3 1 2 4 5
4 3 5
5 3 4
"))
> (greedy-coloring butterfly)
'#hash((5 . 1) (4 . 0) (3 . 2) (2 . 1) (1 . 0))
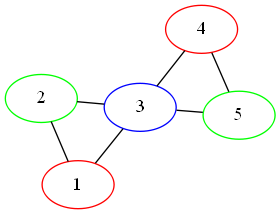
So we assigned the central node a color (3) and then each side two colors (0/1). For this particular case, it turns out that’s actually optimal. But we can come up with a graph where a simple greedy coloring doesn’t work:
> (define loop (read-graph "
6
1 4 6
2 3 5
3 2 6
4 1 5
5 2 4
6 1 3
"))
> (greedy-coloring loop)
'#hash((6 . 2) (5 . 2) (4 . 1) (3 . 1) (2 . 0) (1 . 0))
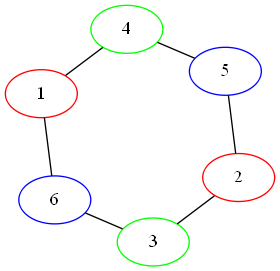
Here, we have three different colors for each of the pairs. The problem is, it’s fairly obvious that there should be a two coloring. Just color every other node:
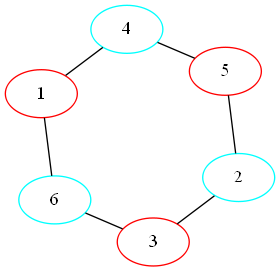
So how should we do it? Well one interesting thing about the greedy coloring is that while the default node order doesn’t give an optimal coloring, there does exist an ordering that does2. So how about we try a bunch of random orderings and take the best? Something like this:
; Try a bunch of random colorings, keeping the best
(define (random-coloring g #:iterations [iterations 1e6])
(define-values (coloring count)
(for/fold ([best-coloring #f] [best-count +inf.0])
([i (in-range iterations)])
(define new-coloring (greedy-coloring g (shuffle (in-vertices g))))
(define new-count (set-count (list->set (hash-values new-coloring))))
(if (< new-count best-count)
(values new-coloring new-count)
(values best-coloring best-count))))
coloring)
Give it a try:
> (random-coloring loop #:iterations 100)
'#hash((6 . 1) (5 . 0) (4 . 1) (3 . 0) (2 . 1) (1 . 0))
That’s pretty shiny. With just a hundred random trials, we’ve found a two coloring. Granted, there are only 720 possible permutations for this particularly graph (6! ), but you could play with the number of iterations.
Still, we should be able to do better.
One interesting comment from the original problem brings up some work from Daniel Brélaz. Essentially, you repeatedly pick the node that has the most already colored neighbors (those will be the hardest to color), breaking ties by the most uncolored neighbors (most likely to need a new color). The way I’ll be implementing that is by assigning a ‘brélaz-number’ to each node:
Basically, we have a two digit number, using the size of the graph as the base. If that doesn’t make sense, we could certainly make a more direct two stage sorting function, but I think it’s sort of elegant. 😄
Anyways, here’s the entire function:
; Use a Brélaz coloring:
; Choose the vertex with the most colored neighbors,
; breaking ties by most uncolored neighbors
(define (brélaz-coloring g)
(define colors (make-hash))
; Used to break ties as mentioned above
(define (count-colored-neighbors n)
(length (filter (curry hash-has-key? colors) (neighbors g n))))
(define (count-uncolored-neighbors n)
(length (filter (negate (curry hash-has-key? colors)) (neighbors g n))))
(define graph-size (length (in-vertices g)))
(define (brélaz-number n)
(+ (* (count-colored-neighbors n) graph-size)
(count-uncolored-neighbors n)))
; Each time, color the node with the highest current brélaz-number (see above)
(for ([i (in-range graph-size)])
(assign-first-color!
g
colors
(first
(sort
(filter (negate (curry hash-has-key? colors)) (in-vertices g))
(λ (n1 n2) (> (brélaz-number n1) (brélaz-number n2)))))))
colors)
(define brelaz-coloring brélaz-coloring)
How does that do on the previous problem?
> (brélaz-coloring loop)
'#hash((6 . 1) (5 . 0) (4 . 1) (3 . 0) (2 . 1) (1 . 0))
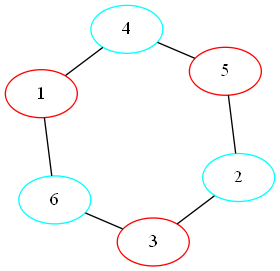
Much better, although either runs quickly enough that on my machine at least you can’t even tell the difference. It will make a difference on much bigger graphs though. For example, let’s try running the various scans on the actual original problem (a coloring of French regions, available
> (define france (with-input-from-file "france.txt" read-graph))
> (greedy-coloring france)
'#hash((46 . 4) (29 . 1) (12 . 3) (72 . 4) (89 . 5) (94 . 4) (79 . 4)
(11 . 2) (26 . 4) (41 . 3) (56 . 2) (78 . 3) (95 . 4) (27 . 2)
(10 . 1) (57 . 0) (40 . 2) (92 . 2) (77 . 3) (43 . 4) (58 . 4)
(9 . 1) (24 . 3) (76 . 1) (93 . 1) (59 . 3) (42 . 2) (25 . 3)
(8 . 2) (7 . 3) (22 . 0) (37 . 0) (52 . 3) (82 . 2) (67 . 3)
(23 . 3) (6 . 2) (53 . 0) (36 . 1) (66 . 0) (83 . 1) (39 . 1)
(54 . 2) (5 . 2) (80 . 2) (65 . 2) (55 . 1) (38 . 1) (21 . 0)
(4 . 0) (64 . 0) (81 . 1) (86 . 3) (71 . 3) (3 . 1) (18 . 0)
(33 . 1) (48 . 0) (70 . 2) (87 . 0) (19 . 2) (2 . 1) (49 . 2)
(32 . 1) (84 . 2) (69 . 0) (35 . 1) (50 . 2) (1 . 2) (16 . 1)
(68 . 1) (85 . 1) (51 . 0) (34 . 0) (17 . 0) (15 . 1) (30 . 1)
(45 . 2) (60 . 0) (90 . 0) (75 . 0) (31 . 0) (14 . 0) (61 . 1)
(44 . 0) (74 . 1) (91 . 1) (0 . 0) (47 . 0) (62 . 0) (13 . 0)
(28 . 0) (88 . 0) (73 . 0) (63 . 0))
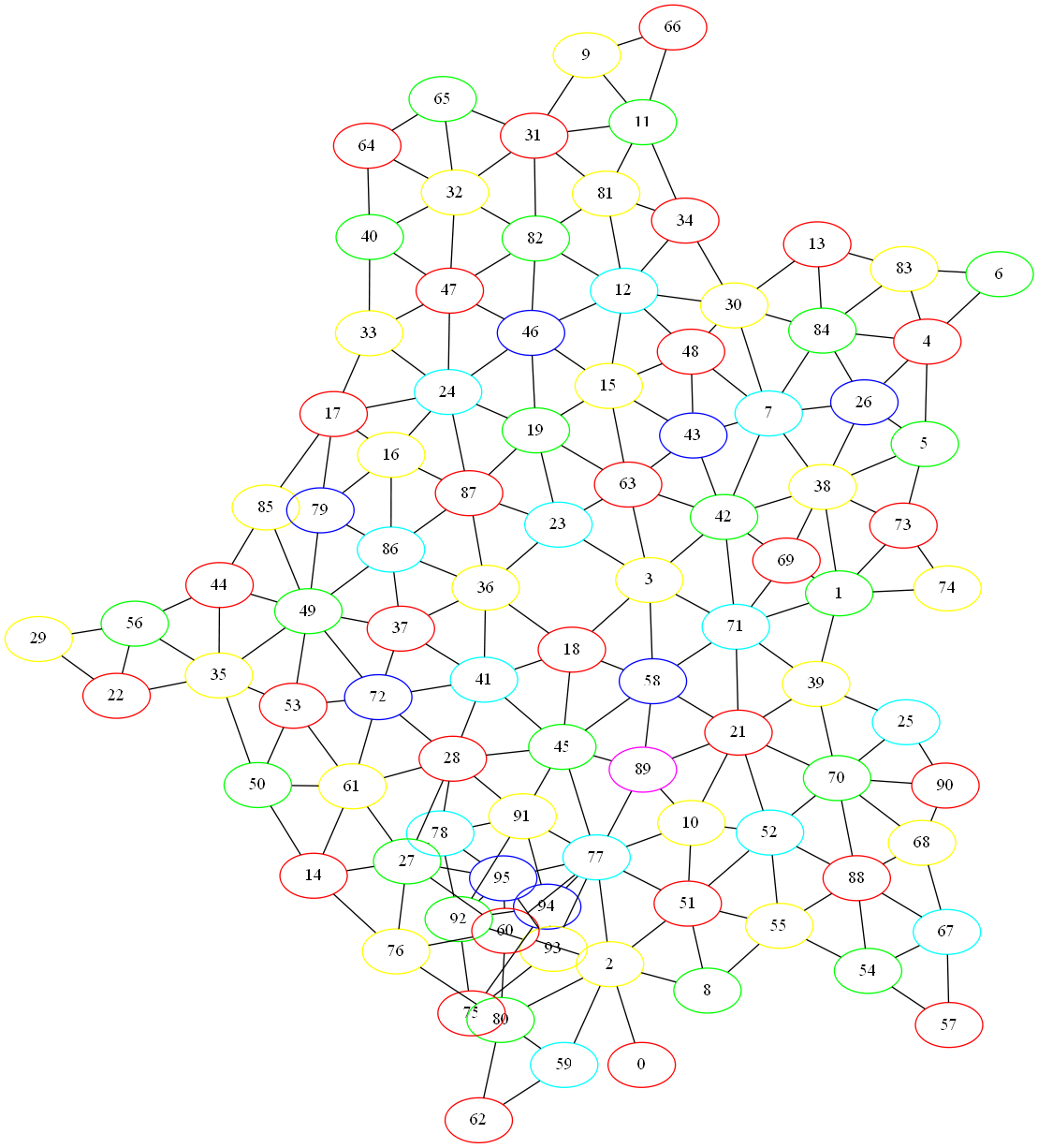
A little messy down there towards the bottom, and not that easy to tell how many colors we have. Looks like six. Let’s go ahead and write a function to tell us how many we actually used:
; Calculate the chromatic number of a graph, potentially given a coloring function
(define (chromatic-number g #:coloring-function [coloring perfect-coloring])
(add1 (apply max (hash-values (coloring g)))))
With the greedy coloring algorithm:
> (chromatic-number france #:coloring-function greedy-coloring)
6
Hmm. Let’s see if Brélaz can do better:
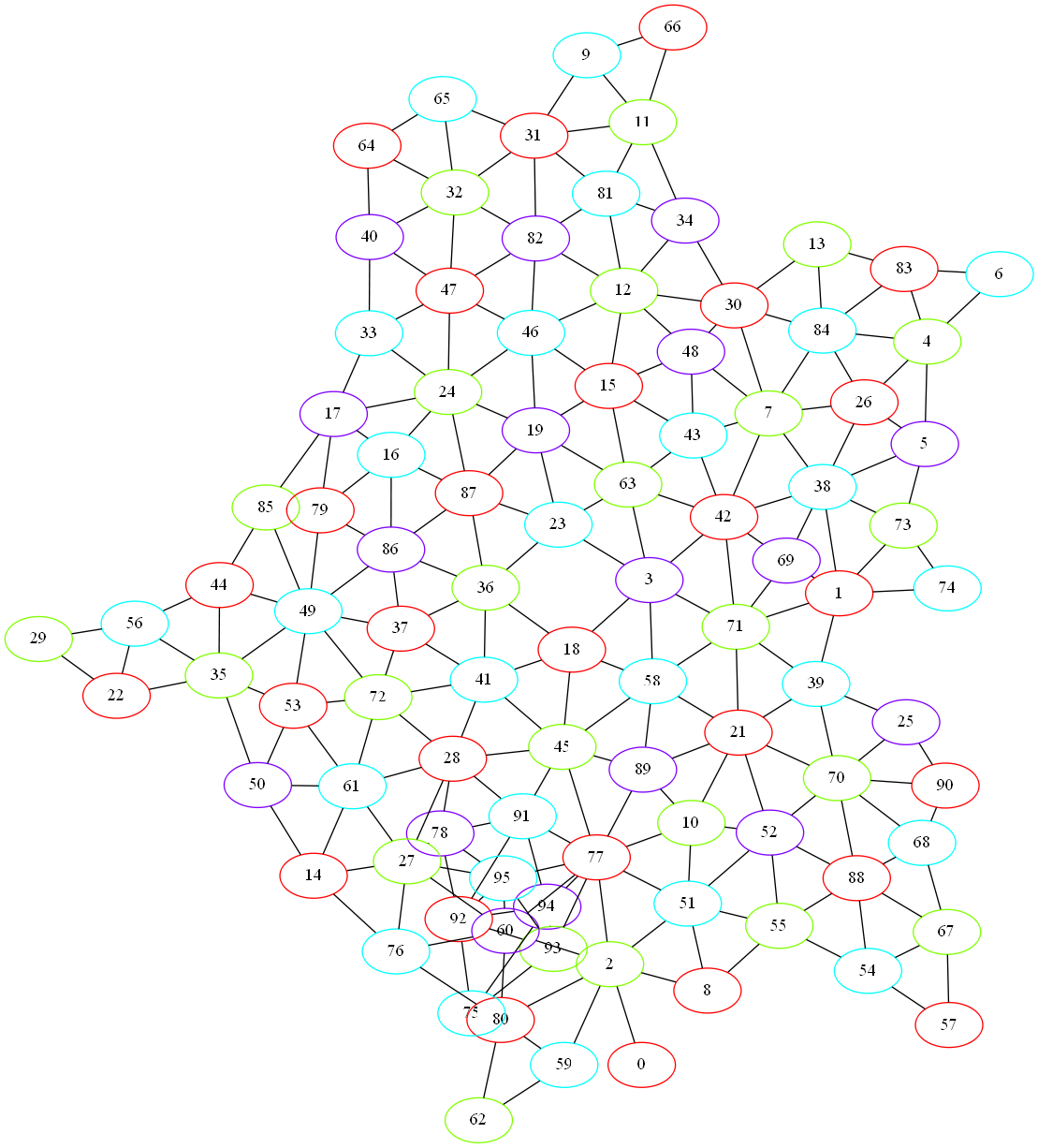
> (chromatic-number france #:coloring-function brélaz-coloring)
4
That’s much better! And given the four color theorem3, that should be an upper bound. Unfortunately, it doesn’t seem that the random coloring is doing any better (at least with my random number generator). Even with 100,000 iterations, the best that it found was 5.
But… what if we want to do it perfectly? Well, if we go through every coloring, we’re guaranteed to find a correctly solution. Of course in Big O notation, that’s O(n!)
which basically is as good as forever… Still, we might as well write the codegenerators
!). 😄
; Try every possible coloring (this is crazy slow)
(define (perfect-coloring g)
; Return all permutations of a given list as a sequence
(define (in-permutations ls)
(local-require racket/generator)
(in-generator
(let loop ([ls ls] [acc '()])
(cond
[(null? ls)
(yield acc)]
[else
(for ([a (in-list ls)])
(loop (remove a ls) (cons a acc)))]))))
; Try each coloring in turn
(define-values (coloring count)
(for/fold ([best-coloring #f] [best-count +inf.0])
([coloring-order (in-permutations (in-vertices g))])
(define new-coloring (greedy-coloring g coloring-order))
(define new-count (set-count (list->set (hash-values new-coloring))))
(if (< new-count best-count)
(values new-coloring new-count)
(values best-coloring best-count))))
coloring)
Basically, we use a generator
to create all of the permutations recursively. With that, we keep going until we have a best coloring. For the loop or butterfly, it works fine:
> (chromatic-number loop #:coloring-function perfect-coloring)
2
> (chromatic-number butterfly #:coloring-function perfect-coloring)
3
Anything bigger… be prepared for a wait.
And that’s pretty much it. I did want to show off one more neat bit of code, designed to output graph files in the format Graphviz expects in order to generate all of the visualizations on this page. Pretty neat stuff and fairly easy to write:
; Output a graph in graphviz / dot format, potentially with coloring
(define (graphviz g
#:coloring-function [coloring #f]
#:horizontal [horizontal #f]
#:save-as-png [save-as-png #f])
; Generate the dot file
(define dot-file
(with-output-to-string
(thunk
(printf "graph G {\n")
; Prefer horizontal layout to vertical
(when horizontal
(printf "\trankdir=LR;\n"))
; Color nodes using evenly spaced HSV colors
(when coloring
(define colors (coloring g))
(define color-count (add1 (apply max (hash-values colors))))
(for ([(node color) (in-hash colors)])
(printf "\t~a [color=\"~a 1.0 1.0\"];\n"
node
(~a #:max-width 5 (exact->inexact (/ color color-count))))))
; Write out all edges (directional, so only if sorted)
(for ([edge (in-edges g)])
(when (< (first edge) (second edge))
(printf "\t~a -- ~a;\n" (first edge) (second edge))))
(printf "}\n"))))
; Either save via buffer file or just return the dot file text
(cond
[save-as-png
(with-output-to-file #:exists 'replace "output.dot" (thunk (display dot-file)))
(system (format "dot output.dot -Kneato -Tpng -s0.5 -o ~a" save-as-png))]
[else
dot-file]))
If you don’t supply a #:save-as-png parameter, you get the graph. Something like this:
> (display (graphviz butterfly #:coloring-function brelaz-coloring))
graph G {
1 [color="0.333 1.0 1.0"];
2 [color="0.666 1.0 1.0"];
3 [color="0.0 1.0 1.0"];
4 [color="0.333 1.0 1.0"];
5 [color="0.666 1.0 1.0"];
1 -- 2;
1 -- 3;
2 -- 3;
3 -- 4;
3 -- 5;
4 -- 5;
}
That’s one of the things I love about the HSV color space. You can just evenly divide the H parameter and you’ll get a bunch of unique colors.
And there you have it. Graph coloring / visualization. I think it’s one of my favorite branches of mathematics. There are just so many interesting things you can do with graphs.
The source code is on GitHub, if you’d like to check it out: graph-coloring.rkt
Technically, NP-complete, as noted in Karp’s 1972 list of 21 NP-complete problems ↩︎
Exercise for the reader: prove this 😄 ↩︎
And assuming that there aren’t any discontinuous regions, which I don’t think is actually the case… ↩︎