(- (- (+ 4 (* 2 7)) (* (- 1 6) 5)) 1)
is the same as
4 + 2 * 7 - (1 - 6) * 5 - 1
is the same as
4 2 7 * + 1 6 - 5 * - 1 -
Madness right?
Not really. More like prefix, infix, and reverse polish / postfix notation. Basically, they’re all just ways of writing down mathematical concepts.
You can really see it if you start with the general structure that all three share:
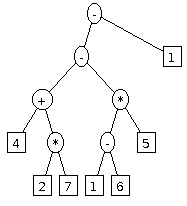
That’s what’s called an expression tree. Each node is either a number (the boxes) or a function of two numbers (the circles). To calculate the final value of the tree, you can either think of it by starting at the top or the bottom and working recursively. If you start at the top, whenever you have an operator, branch and work out the value of the two child trees. When you have those, apply the function. If you start at the bottom, repeatedly find branches that have just a leaf on each side and simplify them. Either way, you’ll get the same answer.
From the expression tree, you can easily get the three expressions that we were dealing with earlier. Just take the preorder, inorder, or postorder traversal of the tree (I’ll cover those algorithms at some point as well).
Then to evaluate the tree, you’ll get something like this (using the prefix notation as it’s textual representation is most similar to the tree structure):
(- (- (+ 4 (* 2 7)) (* (- 1 6) 5)) 1)
= (- (- (+ 4 14) (* -5 5)) 1)
= (- (- 18 -25) 1)
= (- 43 1)
43
Basically, you end up repeated end up rewriting expressions from the inside out until you’re left with the final answer. The same sort of thing happens with the infix notation:
4 + 2 * 7 - (1 - 6) * 5 - 1
= 4 + 14 - -5 * 5 - 1
= 4 + 14 - -25 - 1
= 18 - -25 - 1
= 43 - 1
= 42
This time it’s a little more complicated to figure out which expressions are on the “inside”, but on the flip side it’s easier to understand since we’re all used to working with infix expressions, we’ve been doing them since grade school after all.
What about the Reverse Polish Notation?
4 2 7 * + 1 6 - 5 * - 1 -
= 4 14 + -5 5 * - 1 -
= 28 25 - 1 -
= 43 1 -
= 42
Same thing. Just this time, you’re looking for two numbers followed by an operator which you can then reduce.
So what if a computer wanted to do any of these operations?
Note: In order to make this a fair comparison, the input to each will be a list of either numbers or functions that take two numbers and return one. This means that the prefix code at least will be a little more complicated than just calling eval.
Let’s start with the prefix / Scheme version:
(define (car+cdr ls)
(values (car ls) (cdr ls)))
(define (prefix-calc main-expr)
(define (step expr)
(cond
[(number? (car expr))
(values (car expr) (cdr expr))]
[else
(let*-values ([(op rest) (car+cdr expr)]
[(lv rest) (step rest)]
[(rv rest) (step rest)])
(values ((eval op) lv rv) rest))]))
(let-values ([(val rest) (step main-expr)])
(if (null? rest)
val
(error 'prefix-calc
(format "malformed expression ~s: ~s left over" main-expr rest)))))
~ (prefix-calc '(+ * 5 8 + 5 - 1 4))
42
There are a few interesting bits here, so let’s go through them one by one. The first thing is the helper function, step. Essentially, step’s job is to take one “step” in the given expression. If the first thing is a number, just return it. If it’s an operator we need to find the value of the two sub-expressions and then apply it. To do that, I’ve defined step to take in an expression and return a pair of values: the numeric result of the step and any part of the expression that we did not consume.
That’s where the let*-values comes in. Basically, it threads the three states that the code can be in together:
(let*-values ([(op rest) (car+cdr expr)]
[(lv rest) (step rest)]
[(rv rest) (step rest)])
...)
The first line pulls apart the operator and the rest. The second line applies step again, starting at the cdr of the original list. If step does everything that it’s supposed to (the promise of recursion), then we should get back a value from the front of the list (as lv) and any part of the list we didn’t process (as the first value of rest). We can then feed that rest right back into step, resulting in another value (the right side) and anything that didn’t get processed to give us that. We now have an operator and it’s two arguments lv and rv and anything we didn’t use to calculate any of those (the final value of rest), so return those two values.
Easy enough right? Well, it turns out that combining that with a base case that deals with single numbers is all that you need. Recursion takes care of the rest. But all of that power doesn’t come for free. The drawback of doing this is that you need to allocate a stack frame each time you make the recursive call. Worse yet, it’s not tail recursive so you can’t even make that optimization. Still, it’s a neat bit of code.
The next one gets even more interesting. Here, we have to deal with infix notation. It may be the one that we’ve all grown up with, but it’s actually generally considered the hardest of the three to deal with from a computer’s perspective. Mostly because we have to deal with precedence and associativity to really do it correctly.
The way that I’m going to do it is to repeatedly go through the given expression and evaluate things based on their precedence. So I’ll find the leftmost multiplication or division and combine it, repeating until there are none left. If we didn’t find any, try the leftmost addition or subtraction. After that, go back and try multiplication and division again. It’s definitely not an efficient way to do it, but it does work.
First, the code that will find and reduce one expression of a given type:
(define (step ls which)
(cond
[(number? ls) ls]
[(or (null? ls) (null? (cdr ls)) (null? (cddr ls))) ls]
[(member (cadr ls) which)
(cons ((eval (cadr ls)) (car ls) (caddr ls)) (cdddr ls))]
[else
(cons (car ls) (step (cdr ls) which))]))
~ (step '(1 + 2 * 3 - 4) '(* /))
(1 + 6 - 4)
Then, a function that will repeatedly step, taking precedence into account. This is the slow part. 😄
(define (step-all ls)
(let ([step1 (step ls '(* /))])
(if (equal? ls step1)
(let ([step2 (step step1 '(+ -))])
(if (equal? step1 step2)
(car step2)
(step-all step2)))
(step-all step1))))
~ (step-all '(1 + 2 * 3 - 4))
3
And finally, the glue that holds the parts together:
(define (infix-calc expr)
(define (step ls which) ...)
(define (step-all ls) ...)
(step-all expr))
~ (infix-calc '(4 + 2 * 7 - 1 * 5 + 6 * 5 - 1))
42
(Yes, I had to distribute the 5 at one point. Without doing so, there’s no way to force the subtraction to go first and the expression doesn’t have the same meaning.)
Whew. That was a fun one. Luckily, I’ve saved the easiest one for last. Here, we have the Reverse Polish Notation. As a side note, you have may have guessed that since the other two were prefix and infix notation, another name for RPN is postfix notation.
The algorithm for this one is neat because all you need to keep track of the operation is a stack of values. Whenever you see a number, you push it onto the stack. When you see a function, you pop two values, apply the function, and push the result back onto the stack. Easy as pie. And as an added benefit, you can easily write it in an iterative / tail-recursive manner that avoids allocated stack frames so all the extra memory you need is in the value stack.
(define (postfix-calc expr)
(define (step expr stack)
(cond
[(null? expr) (car stack)]
[(number? (car expr))
(step (cdr expr)
(cons (car expr) stack))]
[else
(step (cdr expr)
(cons ((eval (car expr))
(cadr stack)
(car stack))
(cddr stack)))]))
(step expr '()))
~ (postfix-calc '(4 2 7 * + 1 6 - 5 * - 1 -))
42
Pretty much the only thing you have to watch out for in this code is the actual evaluation:
((eval (car expr)) (cadr stack) (car stack))
Because you pushed the first argument onto the stack first, you have to reverse them after popping them (thus cadr before car). This doesn’t matter for + or *, so it’s easy to miss, but it will really mess up your day when you’re working with - or /.
So there you have it. Three ways to write expressions and at least one way a computer could deal with each of them.
Before I go, I bet you were wondering why postfix notation is more commonly called Reverse Polish Notation. It’s mostly because of Jan Łukasiewicz, a Polish logician and philosopher from first half of the 1900s. Essentially, he described (prefix) Polish notation in the 1920s but for whatever reason it stuck on the postfix notation, ergo reverse. And now you know.
The goal tomorrow is to create a web-based simulation of each of these three algorithms that shows the internal works, step by step. We’ll see how that goes.
If you’d like to download today’s source, you can do so here: source code