Wombat IDE - Turtle graphics

As I mentioned in my last post, I’ve been adding a turtle graphics library to Wombat to use with the other C211 libraries (matrix, image, and tree).

Edit: The most recent C211 APIs can be found here:

Edit: This post used an old version of the turtle graphics API, specifically using the function spawn rather than hatch in the code examples. So that the code will run in the newer version of Wombat, I have updated the examples.

Essentially, to think about turtle graphics, consider as a thought experiment a turtle standing in the middle of a giant blank white sheet of paper. Tied to the turtle’s tail is a marker, initially in black. From there, you can issue a series of commands to the turtle, for example, telling it to move! or to turn-left! or turn-right!. You can also tell the turtle to lift-pen! and stop drawing, drop-pen! and start again, or even set-pen-color! to change to a different marker. Finally, there are some meta commands that allow you to either split into more turtles that will work in parallel, to run a block of commands and then reset back to the original state, or even to repeat a series of commands. For anything else, just check out the API:

`(c211 turtle)` API

Creating turtles:

(hatch) - create a new turtle
(hatch dir) - create a new turtle with the given facing (in degrees, 0 is north, positive to the right / clockwise)
(hatch x y) - create a turtle at the point (x, y) instead of the origin
(hatch x y dir) - create a turtle at (x, y) with the given facing
(hatch x y dir up/down color) - create a turtle at (x, y) with the given facing and a color pen that is either up or down
(split t) - create a copy of a turtle so that the two can move in parallel (for branching structures)

Movement:

(move! t n) - move the turtle n units in whichever direction it is facing; draw a line if the pen is down
(move-to! t x y) - jump directly to the point (x, y), preserving the original facing; draw a line if the pen is down
(turtle-location t) - return the turtle’s current location as a list of the form (x y)
(turn-left! t d) - turn left / counter-clockwise this many degrees.
(turn-right! t d) - turn right / clockwise this many degrees
(turn-to! t d) - turn directly to a given facing (in degrees, 0 is north, positive to the right / clockwise)
(turtle-direction t) - return the turtle’s current facing

Drawing:

(lift-pen! t) - lift the turtle’s pen and stop drawing
(drop-pen! t) - drop the turtle’s pen and start drawing again
(pen-up/down? t) - return either up if the pen is up or down if it’s down
(set-pen-color! t c) - set the turtle’s pen’s color; colors can be accessed from (c211 image)
(pen-color t) - access the turtle’s pen’s current color as a color from (c211 image)

Output:

(draw-turtle t) - draw the turtle and any turtles split from it to the screen; if this turtle was the result of a split, its parent will not be drawn
turtle->image - convert the turtle to an image from (c211 image), (draw-turtle t) is equivalent to (draw-image (turtle->image t))

Useful macros:

(block t cmds ...) - save the turtle’s current state then execute a series of commands; then reset the turtle to the stored state
(repeat n cmds ...) - repeat a series of commands n times; does not restore turtle state

To use the turtle graphics library, you will have to import it with (import (c211 turtle)). After that, just give the above commands a try.

Examples

Here are some interesting turtles that I’ve written/translated from the Wikipedia page on L-Systems.

Box:

To start out with, a simple box. This shows how to move, how to turn, and how to use the repeat macro. In this example and all of the following ones, a new turtle is hatched when calling the function and returned at the end. The functions could have been written to take a turtle as an argument, alter its state, and return nothing–that’s just not how I did it.

(define box
  (lambda ()
    (let ([t (hatch)])
      (repeat 4
        (move! t 100)
        (turn-right! t 90))
      t)))

(draw-turtle (box))

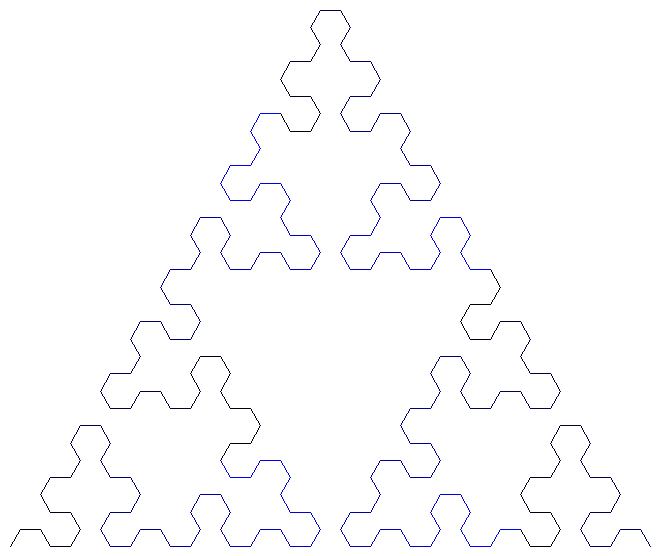
Sierpinski triangle:

Next, the traditional Sierpinski triangle. This is based on the L-systems Wikipedia page, using function calls for the recursive generating function. The original two inverse calls have been combined into the single loop, using the sign of the variable d to control which way the rotation is currently going.

(define sierpinski
  (lambda (n) 
    (let ([t (hatch)])
      (turn-right! t 30)
      (let loop ([i 0] [d 60])
        (if (= i n)
            (begin
              (set-pen-color! t
                (color 0 0 (mod (+ (color-ref 
                                     (pen-color t) 
                                     'blue)
                                   (random 10))
                             256)))
              (move! t 20))
            (begin
              (loop (+ i 1) (- d))
              (turn-right! t d)
              (loop (+ i 1) d)
              (turn-right! t d)
              (loop (+ i 1) (- d)))))
      t)))

(draw-turtle (sierpinski 5))

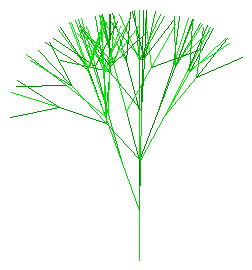
Recursive tree:

A simple tree that starts with a single turtle and splits into two additional turtles at each iteration. Using a proper rendering (which I haven’t actually written yet), you could see all of the branches expanding outwards in parallel.

(define tree
  (lambda (n)
    (let ([t (hatch)])
      (let loop ([i 0] [t t])
        (when (< i n)
          (set-pen-color! t (color 0 (+ 128 (random 128)) 0))
          (move! t 50)
          (let ([l (split t)]
                [r (split t)])
            (loop (+ i 1) t)
            (turn-left! l (random 45))
            (loop (+ i 1) l)
            (turn-right! r (random 45))
            (loop (+ i 1) r))))
      t)))

(draw-turtle (tree 5))

Recursive star:

Rather than using split as the tree above does, this star uses a combination of repeat (to get the multiple arms) and block (to reset to the center for new extension).

(define star
  (lambda (p n)
    (let ([t (hatch)])
      (let loop ([i 0] [d 100])
        (when (< i n)
          (set-pen-color! t (color 0 (div (* 255 i) n) 0))
          (repeat p
            (turn-right! t (/ 360 p))
            (block t
              (move! t d)
              (loop (+ i 1) (/ d 2))))))
      t)))

(draw-turtle (star 5 3))

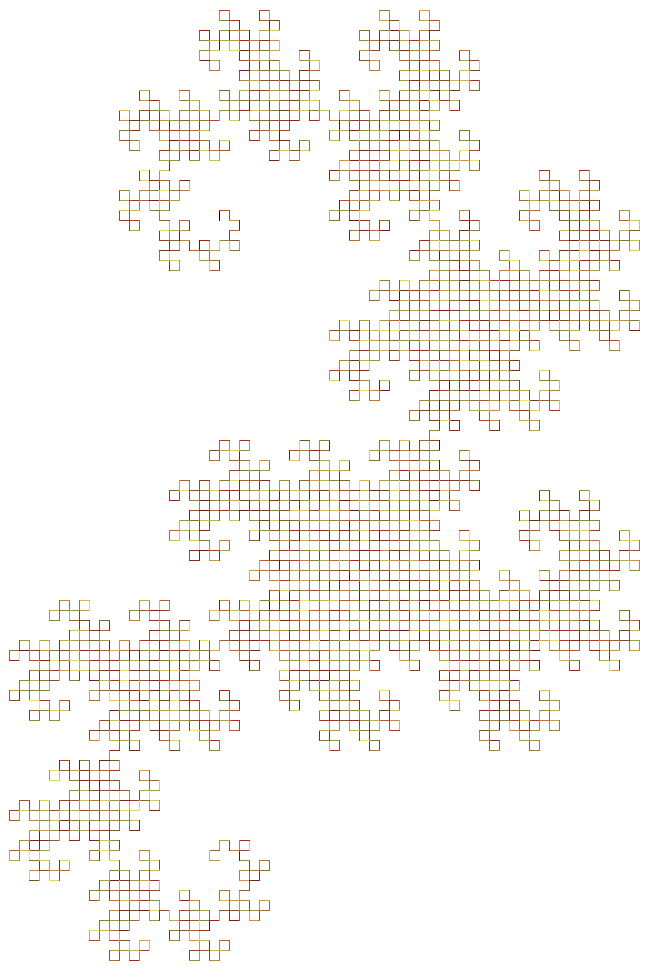
Dragon fractal:

This is a pretty fractal translated almost directly from the L-System Wikipedia page. Each recursive level became a function directly this time. The coloring is randomly selected tones from yellow to red.

(define dragon
  (lambda (n)
  (let ([t (hatch)]
        [angle 90]
        [distance 10])
    (define (f)
      (set-pen-color! t
        (let* ([r (+ 128 (random 128))]
               [g (min r (random 255))]
               [b 0])
          (color r g b)))
      (move! t distance))
    (define (x i)
      (when (< i n)
        (x (+ i 1))
        (turn-right! t angle)
        (y (+ i 1))
        (f)))
    (define (y i)
      (when (< i n)
        (f)
        (x (+ i 1))
        (turn-left! t angle)
        (y (+ i 1))))
    (turn-left! t 90)
    (move! t distance)
    (x 0)
    t)))

(draw-turtle (dragon 12))

(c211 turtle) API