Overview
As a set of benchmarks to test whether or not the new AnnGram algorithm is actually working correctly, I’ve been trying to come up with different yet similar methods to compare it too. Primarily, there are two possibilities:
- Replace the nGram vectors with another form
- Process the nGrams using something other than Self-Organizing Maps
I’m still looking through the related literature to decide if there is some way to use something other than the nGrams to feed into the SOM; however, I haven’t been having any luck. So far, most of my work has been focused on comparing SOM to k-means clustering.
**K-Means Clustering **
From Wikipedia:
In statistics and machine learning, k-means clustering is a method of cluster analysis which aims to partition n observations into k clusters in which each observation belongs to the cluster with the nearest mean. It is similar to the expectation-maximization algorithm for mixtures of Gaussians in that they both attempt to find the centers of natural clusters in the data.
Essentially, k-means clustering turns a set of data in an n-dimensional space (like the nGram input) into a set of clusters such that similar objects are grouped together.
Does it work?
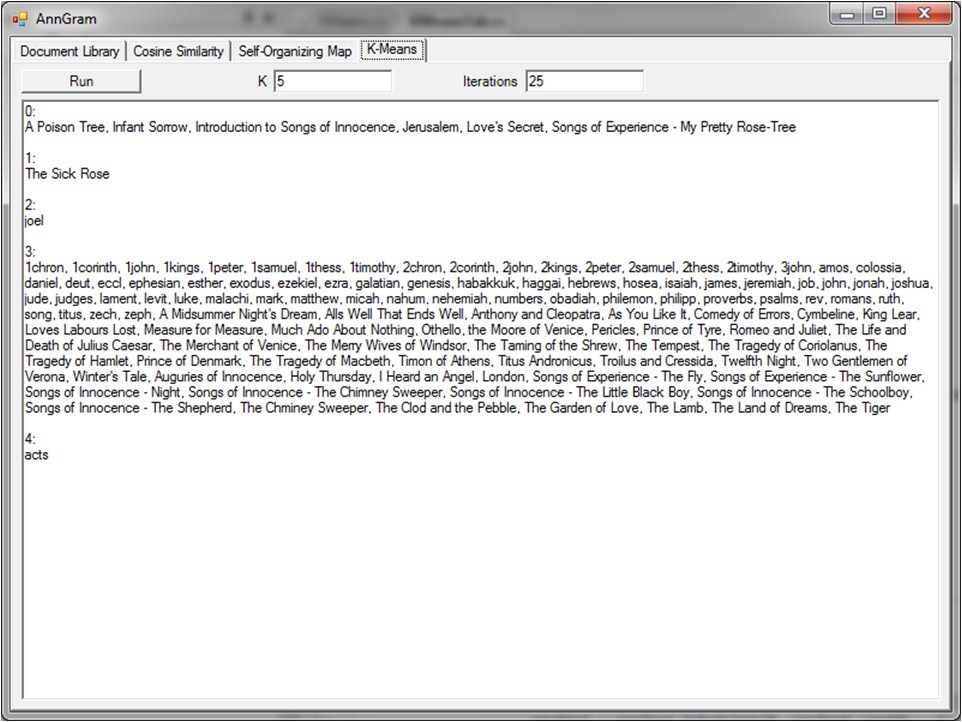
Long story short: It sort of works. For the example, I used 25 iterations and 5 clusters because using fewer clusters had not been returning any distinct group.
I say that it work of works because all of the documents in group 0 are by William Blake. It’s not all of Blake’s work and there is no distinction between the Bible and Shakespeare, but there is at least a little distinction.
For those of you wondering, the single document in each of groups 1, 2, and 4 are because those groups were assigned that particular document to act as their center at some point during the algorithm and it didn’t move. Thus, those particular documents form the center of their “clusters.”
Result
The results are bad for K-Means clustering and good for my algorithm. At the very least, it shows that the combination of nGrams and a SOM is superior to nGrams and K-Means clustering.