In the past, I absolutely loved messing around with genetic algorithms. The idea of bringing the power of natural selection to bear to solve all manner of problems just appeals to me for some reason. So when I came across a puzzle on on Programming Praxis called flibs source code
The eventual goal will be–given a binary sequence–to evolve a finite state machine that will recognize the sequence and output the same, offset by one. So if we’re given the sequence 010011010011, the solution will output something like this: 001001101001.
So what do we need to do this? First, we need a way to represent the finite automaton. We’re just going to directly go with what they suggested in the post and build machines with three states. So for example, this would be a valid machine:
| Input 0 | Input 1 | |||
|---|---|---|---|---|
| A | 1 | B | 1 | C |
| B | 0 | C | 0 | B |
| C | 1 | A | 0 | A |
Which is equivalent to this diagram:
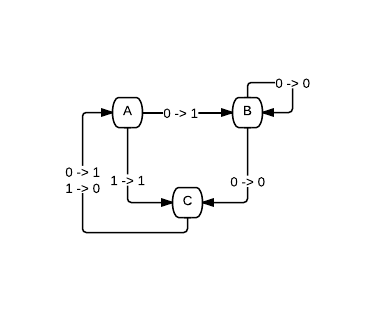
So how can we represent this in code? I went with a vector just writing straight across the rows and then down the columns. So the chart represented above then becomes this vector:
'#(1 B 1 C 0 C 0 B 1 A 0 A)
Given a flib and an input (also represented as a vector), how do we generate the output?
; run a flib on a given input
(define (run-flib flib input)
; turn a state into a number
(define (f s) (case s [(A) 0] [(B) 1] [(C) 2]))
; initial state
(define state 'A)
; loop over the flip, update state and report output
(for/vector ([this input])
(let ([next (vector-ref flib (+ (* (f state) 4) (* this 2) 1))]
[output (vector-ref flib (+ (* (f state) 4) (* this 2)))])
(set! state next)
output)))
Basically, keep a mutable state starting at A. At each tick, pull apart the rows in the vector structure from above to get the output for the current state and input, along with the next input. Each enough, but still nothing like a genetic algorithm.
The general idea of the algorithm is to generate a random initial population then repeatedly mutate and breed those individuals until the population improves enough to find an optimal solution. So the first thing we need is a way to generate random flibs. Easy enough with for/vector:
; generate a random flib
; a flib is a state machine of the form
; 0 1
; A 1B 1C
; B 0C 0B
; C 1A 0A => 1B1C0C0B1A0A
(define (random-flib)
(for/vector ([i 12])
(if (even? i)
(random 2)
(vector-ref '#(A B C) (random 3)))))
After that, we need to calculate the fitness of each individual in the population. The strongest individuals will survive, the weaker ones will die off. So here’s a function that will take an flib and an input vector, run the flib using the function above, and then measure the difference (offset by 1 as noted above).
; score a flib by calculating it's output, shifting one right
; and counting differences
(define (score-flib flib input)
(define output (run-flib flib input))
(- 1.0 (/ (for/sum ([i (- (vector-length input) 1)])
(abs (- (vector-ref input (+ i 1))
(vector-ref output i))))
(- (vector-length input) 1))))
That’s enough to tell us which the stronger individuals are, but how do we use that to improve the population? Two different ways. First, we want to be able to take two individuals together and “breed” them. In the example given, they suggested breeding the strongest and weakest individual and using that to replace the weakest, but there are many possible strategies. The one I went for was to remove the lowest (given) number from a population and then breeding surviving members at random to get back to the original population size. We’ll see that later in the run function.
; breed two flibs by selecting a crossover point and merging input
(define (breed flib1 flib2)
(define @ (random (vector-length flib1)))
(for/vector ([i (vector-length flib1)]
[c1 flib1]
[c2 flib2])
(if (< i @) c1 c2)))
The other option for advancement will mostly be used to break out of local optimums. With just crossovers, eventually a population is likely to stagnate as the individuals become too similar. So here we’ll occasionally mutate an flib by randomly tweaking one of the genes therein.
; mutate a flib by random altering one character
(define (mutate flib)
(define @ (random (vector-length flib)))
(for/vector ([i (vector-length flib)]
[c flib])
(if (= @ i)
(if (symbol? c)
(vector-ref '#(A B C) (random 3))
(random 2))
c)))
And with that, we’re as good as done. I added a few more functions to help, for example to turn a string into a vector like the ones we want, which you can here: flibs source code. And without further ado, here’s the main function:
; use a genetic algorithm to find a perfect flib
(define (run input
[pool-size 12] ; number of flibs to breed
[kill-off 2] ; remove the lowest this many flibs each generation
; refill by breeding two random surviving flibs
[mutate-% 0.1]) ; mutate this percentage of flibs each generation
; sort a pool by a given criteria
(define (sort-pool pool)
(sort
pool
(lambda (p1 p2) (> (car p1) (car p2)))))
; iterate until we have a winner
(let loop ([pool (sort-pool
(for/list ([i pool-size])
(let ([flib (random-flib)])
(list (score-flib flib input) flib))))]
[high-score 0])
; find a new maximum
(define new-max (> (caar pool) high-score))
(define next-high-score (if new-max (caar pool) high-score))
(define high-flib (cadar pool))
; display progress
(when new-max
(printf "new best flib: ~s scoring ~s\n" high-flib next-high-score))
; loop (or not)
(if (< next-high-score 1)
(loop
; kill off and replace the lowest performing flibs for the new pool
(sort-pool
(append
; add new flibs by breeding the old ones
(for/list ([i kill-off])
(let ([flib1 (cadr (list-ref pool (- pool-size kill-off)))]
[flib2 (cadr (list-ref pool (- pool-size kill-off)))])
(let ([flib3 (breed flib1 flib2)])
(list (score-flib flib3 input) flib3))))
; randomly mutate surviving flibs the given percent of the time
(for/list ([sflib (drop (reverse pool) kill-off)])
(if (< (random) mutate-%)
(let ([f (mutate (cadr sflib))])
(list (score-flib f input) f))
sflib))))
next-high-score)
high-flib)))
Hopefully it should be pretty self explanatory, particularly with the comments I’ve included, but there are definitely some more interesting bits. For example, the pool is going to be maintained as a list of pairs. Each pair has the score of an flib and then the flib in question to make sorting easier (without recalculating the score whenever we want to sort).
The next interesting part is the loop. Each iteration, we’ll have a sorted list, so we’ll check for the highest scoring flib currently in the pool. If it’s better than what we’ve seen, print that out and remember it. Otherwise, just keep going.
The bulk of work of updating the generation takes place in the recursive call to loop. We’ll use drop to remove the weakest parts of the population (after a reverse so that they’re at the front of the list) and then append on the newly bred members with their randomly selected parents.
And that’s actually all there is to it. Here’s an example of running it:
> (run (string->input (repeat-string "010011" 5)))
new best flib: #(1 C 1 C 1 B 1 A 1 A 0 A) scoring 0.8275862068965517
new best flib: #(1 B 1 A 0 C 0 B 1 A 0 A) scoring 0.8620689655172413
new best flib: #(1 A 1 C 1 B 0 C 0 A 0 B) scoring 0.9655172413793104
new best flib: #(1 C 0 A 0 C 1 A 1 B 0 B) scoring 1.0
'#(1 C 0 A 0 C 1 A 1 B 0 B)
Not the same machine we had above, but they both represent the string. If we run the same thing again, we’re likely to get another equivalent result:
> (run (string->input (repeat-string "010011" 5)))
new best flib: #(1 C 0 C 1 B 0 B 1 A 1 C) scoring 0.6551724137931034
new best flib: #(1 C 1 A 1 C 0 B 1 A 0 A) scoring 0.6896551724137932
new best flib: #(1 A 1 B 0 A 0 A 0 A 1 B) scoring 0.8275862068965517
new best flib: #(1 C 1 C 0 C 1 B 1 A 0 B) scoring 0.8620689655172413
new best flib: #(1 B 0 C 1 A 1 C 0 A 0 B) scoring 0.9655172413793104
new best flib: #(1 A 0 C 1 B 1 C 0 B 0 A) scoring 1.0
'#(1 A 0 C 1 B 1 C 0 B 0 A)
Alternatively, we can tweak the other parameters. Say we wanted a larger population with a 1/5 killoff rate and twice the mutation rate:
> (run (string->input (repeat-string "010011" 5)) 25 5 0.2)
new best flib: #(1 A 0 C 0 B 0 A 0 A 1 A) scoring 0.6896551724137932
new best flib: #(0 C 1 C 1 C 1 C 1 A 0 A) scoring 0.8275862068965517
new best flib: #(0 C 0 A 1 A 0 B 1 C 1 B) scoring 0.8620689655172413
new best flib: #(0 B 1 C 1 A 0 A 1 B 0 C) scoring 0.9655172413793104
new best flib: #(1 A 0 B 0 C 0 A 1 C 1 B) scoring 1.0
'#(1 A 0 B 0 C 0 A 1 C 1 B)
That’s one of the fun parts about genetic algorithms is tuning the parameters. Any given problem can have vastly different sets of optimal parameters.
In any case, that’s all I have for now. I’ve started working on a version that will generalize to any string (with only three states, this can only recognize strings with a limited length), but progress is proving rocky. We’ll see how it goes.
If you would like the source code, you can get it here: flibs source code
If you have any questions or comments, drop me a line below.