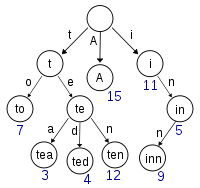
For the next few posts, we’re going to need a way to represent a dictionary. You could go with just a flat list containing all of the words in the dictionary, but the runtime doesn’t seem optimal. Instead, we want a data structure that lets you easily get all possible words that start with a given prefix. We want a trie.